
这段代码的主要作用是计算图像的单应性矩阵,并使用该矩阵对图像进行透视变换。具体来说,它的功能包括:
1. **单应性矩阵估计**:
- 使用给定的四对对应点(通常是从源图像和目标图像提取的特征点),计算出一个3x3的单应性矩阵。这个矩阵描述了从源图像到目标图像的平面映射关系。
2. **图像透视变换**:
- 利用计算出的单应性矩阵对源图像进行透视变换,从而将源图像中的某一平面变换为目标图像中的对应平面。这个过程可以校正图像中的透视失真,或者进行图像配准等操作。
3. **结果展示**:
- 变换后的图像通过`matplotlib`进行显示,展示了透视变换的结果。这通常用于验证单应性矩阵的计算是否正确,以及变换效果是否符合预期。
这种操作在计算机视觉中非常常见,特别是在图像拼接(如全景照片生成)、图像校正(如去除相机角度导致的失真)以及增强现实应用中。
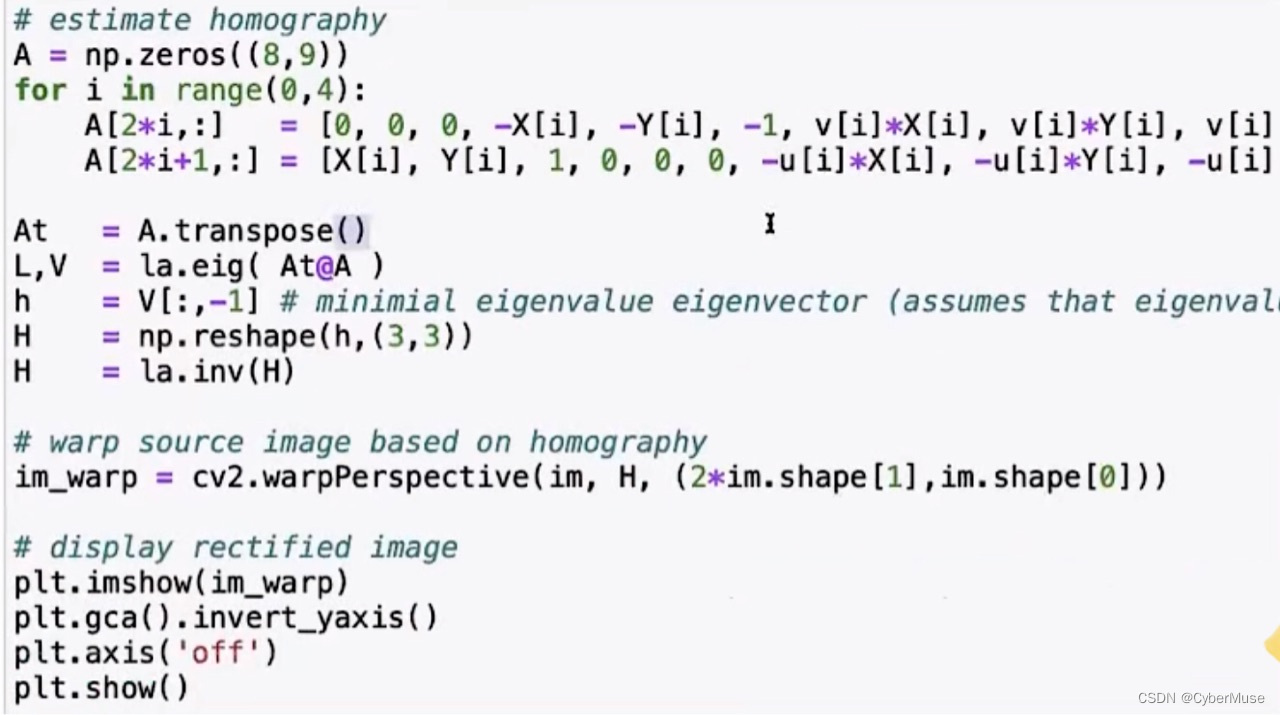
以下是校对后的代码版本:
```python
import numpy as np
import cv2
import matplotlib.pyplot as plt
# estimate homography
A = np.zeros((8, 9))
for i in range(0, 4):
A[2*i, :] = [0, 0, 0, -X[i], -Y[i], -1, v[i]*X[i], v[i]*Y[i], v[i]]
A[2*i+1, :] = [X[i], Y[i], 1, 0, 0, 0, -u[i]*X[i], -u[i]*Y[i], -u[i]]
At = A.transpose()
L, V = np.linalg.eig(At @ A)
h = V[:, -1] # minimal eigenvalue eigenvector (assumes that eigenvalue is sorted)
H = np.reshape(h, (3, 3))
H = np.linalg.inv(H)
# warp source image based on homography
im_warp = cv2.warpPerspective(im, H, (2*im.shape[1], im.shape[0]))
# display rectified image
plt.imshow(im_warp)
plt.gca().invert_yaxis()
plt.axis('off')
plt.show()
```
### 代码解释
1. **导入库**:
```python
import numpy as np
import cv2
import matplotlib.pyplot as plt
```
- 导入必要的库,`numpy`用于数值计算,`cv2`用于图像处理,`matplotlib.pyplot`用于图像显示。
2. **估计单应性矩阵**:
```python
A = np.zeros((8, 9))
```
- 创建一个8x9的零矩阵`A`,用于存放线性方程组的系数。
```python
for i in range(0, 4):
A[2*i, :] = [0, 0, 0, -X[i], -Y[i], -1, v[i]*X[i], v[i]*Y[i], v[i]]
A[2*i+1, :] = [X[i], Y[i], 1, 0, 0, 0, -u[i]*X[i], -u[i]*Y[i], -u[i]]
```
- 填充矩阵`A`的行。每组点对提供两行数据,分别对应单应性条件的两个方程,`(X[i], Y[i])`是源图像的坐标,`(u[i], v[i])`是目标图像的坐标。
3. **计算特征值和特征向量**:
```python
At = A.transpose()
L, V = np.linalg.eig(At @ A)
```
- 计算`At @ A`的特征值`L`和特征向量`V`。特征向量用于求解单应性矩阵。
4. **提取单应性矩阵**:
```python
h = V[:, -1] # minimal eigenvalue eigenvector
H = np.reshape(h, (3, 3))
```
- 提取最小特征值对应的特征向量`h`,并将其重塑为3x3矩阵`H`。
5. **计算单应性矩阵的逆**:
```python
H = np.linalg.inv(H)
```
- 计算单应性矩阵`H`的逆,用于从目标图像到源图像的反向映射。
6. **应用单应性矩阵进行图像变换**:
```python
im_warp = cv2.warpPerspective(im, H, (2*im.shape[1], im.shape[0]))
```
- 使用OpenCV的`warpPerspective`函数应用单应性矩阵对图像`im`进行透视变换。输出图像的宽度为原图像的两倍,高度保持不变。
7. **显示变换后的图像**:
```python
plt.imshow(im_warp)
plt.gca().invert_yaxis()
plt.axis('off')
plt.show()
```
- 使用`matplotlib`显示变换后的图像,反转y轴并关闭坐标轴以便更好地查看图像。
确保在实际使用中定义和初始化`X`, `Y`, `u`, `v`以及`im`等变量,以避免运行时错误。
当然,这段代码涉及一些具体的技术和数学概念,下面是与代码直接相关的先修知识:
### 1. Python 编程
- **数组操作**:使用 NumPy 进行数组创建和操作,特别是通过 `np.zeros` 创建零矩阵。
- **循环和索引**:使用 `for` 循环来遍历索引并填充矩阵。
### 2. NumPy 和线性代数
- **矩阵构造**:了解如何根据给定的点对构造用于计算单应性的矩阵 `A`。矩阵 `A` 是通过循环根据点的坐标 `(X[i], Y[i])` 和 `(u[i], v[i])` 填充的。
- **特征值分解**:使用 `np.linalg.eig` 计算矩阵的特征值和特征向量,特别是如何从特征向量中选择对应于最小特征值的特征向量作为解。
- **矩阵重塑和逆矩阵**:使用 `np.reshape` 调整特征向量的形状,并使用 `np.linalg.inv` 计算矩阵的逆。
### 3. OpenCV 图像处理
- **图像变换**:使用 `cv2.warpPerspective` 将源图像根据计算得到的单应性矩阵 `H` 进行透视变换。
- **图像大小设置**:变换后的图像大小设置为原始图像宽度的两倍和原始高度。
### 4. Matplotlib 图像显示
- **图像显示**:使用 `plt.imshow` 显示处理后的图像,理解如何通过 `plt.gca().invert_yaxis()` 调整显示坐标轴的方向。
- **隐藏坐标轴**:通过 `plt.axis('off')` 隐藏图像的坐标轴以清晰展示图像。
### 5. 数学基础
- **单应性(Homography)**:理解单应性矩阵的计算,它通过将四对点的坐标映射来进行求解。
- **齐次坐标转换**:将二维点坐标表示为齐次坐标,以便进行透视变换。
### 6. 实践经验
- **调试**:能够识别并修正代码中的潜在错误,例如确保矩阵计算中的维度匹配。
- **优化**:理解如何优化图像处理的效率,特别是在大图像或高分辨率图像的情况下。
这些知识点直接关联到代码的每一部分,帮助理解如何构建和使用单应性矩阵进行图像变换,以及如何有效地处理和显示图像。
当然,我们可以通过一个更加详细的讲课稿来介绍单应性矩阵和齐次坐标的概念,并结合具体的应用实例来帮助理解。这将帮助听众更好地掌握这些技术在实际中的应用。
---
大家好!今天我要讲解的是单应性矩阵和齐次坐标转换,这些是计算机视觉和图像处理中的重要工具。通过具体的应用实例,我希望大家能够对这些概念有更深入的理解。
### 单应性(Homography)
首先,让我们深入了解单应性矩阵。单应性矩阵是一种用来描述两个平面之间的投影变换的工具。在实际应用中,它经常用于图像拼接、校正相机拍摄的透视变形、以及增强现实应用中。
#### 实际应用实例:全景图像拼接
1. **问题背景**:想象一下你正在拍摄一组相邻的照片,希望将它们无缝拼接成一个全景图。这在旅游摄影和虚拟现实中非常常见。
2. **点对选择**:我们从每张图片中选择一些关键特征点。例如,在两个重叠的照片中,我们可以选择建筑物的角落或其他明显的点。
3. **计算单应性矩阵**:使用这些点对,我们可以计算出单应性矩阵。这一步通常依赖于图像特征匹配算法,如 SIFT 或 ORB,来找到这些对应的点。
4. **图像变换**:一旦我们计算出单应性矩阵,就可以将一张图片变换到与另一张图片的坐标系一致,然后进行拼接。通过 OpenCV 中的 `warpPerspective` 函数,我们可以实现这个变换。
5. **实际操作**:让我们在电脑上操作一下。大家可以看到,我将两张重叠的图片导入软件,然后通过标记几个对应点来计算单应性矩阵。计算完成后,软件会自动调整第二张图片的位置和角度,使其与第一张图片完美对齐。
### 齐次坐标转换
接下来,我们讨论齐次坐标。这种表示方法在计算机视觉中非常有用,因为它能简化许多几何变换的计算,特别是对于透视变换。
#### 实际应用实例:透视校正
1. **问题背景**:假设你拍摄了一张建筑物的照片,但是由于拍摄角度,建筑物的边缘看起来不是直的。我们可以使用齐次坐标来纠正这种透视失真。
2. **齐次坐标表示**:在二维空间中,点 `(x, y)` 可以表示为 `(x, y, 1)`。这种表示方式使得我们可以使用矩阵乘法来进行平移、旋转、缩放等操作。
3. **透视变换**:通过调整齐次坐标中的第三个参数,我们可以实现透视变换。这对于矫正图像中的倾斜和失真非常有用。
4. **实际操作**:现在,我会展示如何使用齐次坐标进行透视校正。我们将一张倾斜的建筑物照片导入软件,通过调整齐次坐标的参数来使建筑物的边缘变得垂直。
5. **从齐次到普通坐标**:完成变换后,我们可以将齐次坐标转换回普通坐标,得到校正后的图像。这一步是通过除以齐次坐标的最后一个元素来实现的。
### 结合应用:增强现实
最后,让我们看看一个结合应用实例:增强现实(AR)。
1. **问题背景**:在增强现实应用中,我们需要将虚拟对象准确地叠加在现实世界的场景中。这涉及到精确的坐标变换和图像处理。
2. **使用单应性和齐次坐标**:通过摄像头获取的图像,我们可以识别出场景中的平面,并计算出对应的单应性矩阵。利用齐次坐标,我们可以将虚拟对象的坐标转换到这个平面上。
3. **实际操作**:假设我们要在桌面上显示一个虚拟的三维模型。首先,我们拍摄桌面的图片,标记出桌面的四个角点。然后,计算单应性矩阵,将模型的平面坐标转换到图片的坐标系中。这样,虚拟模型就可以在正确的视角下叠加到真实场景中。
【注】
### 单应性(Homography)
首先,我们来看看单应性矩阵。想象一下,你正在拍摄一个宽阔的全景图,或者想将一个广告牌的图像精确贴合到视频中的建筑上。单应性矩阵正是帮助你完成这些任务的利器。
1. **实际应用**:通过单应性,我们可以将一个平面上的点映射到另一个平面上。这在全景拼接、图像校正和投影映射中非常重要。
2. **四对点映射**:我们需要至少四对对应点来计算单应性矩阵。这些点可以来自图像的不同视角。比如,我们可以在白板上标出这些点,然后看看如何通过这些点进行计算。
3. **动手演示**:现在,让我们动手试一试。我会用这台设备拍摄一张图片,标出四个关键点,然后我们会通过软件来计算出单应性矩阵。您将看到图像如何通过这个矩阵进行变换。
### 齐次坐标转换
接下来,我们讨论齐次坐标。齐次坐标的引入使得我们能够更方便地处理图像中的几何变换。
1. **基本概念**:在二维平面中,一个点 `(x, y)` 可以表示为 `(x, y, 1)`。这个额外的维度允许我们进行更加复杂的变换,比如透视变换。
2. **动手实验**:我会给大家一些点的坐标,大家可以尝试将它们转换为齐次坐标。然后,我们来看看如果改变最后一个坐标会发生什么。
3. **视觉化展示**:通过这段动画,我们可以看到点在齐次坐标下如何进行缩放和透视变换。这种方法使得我们的变换计算更加简单和统一。
4. **从齐次到普通坐标**:最后,我们会展示如何从齐次坐标返回到普通坐标。记住,这种转换是非常有用的,特别是在处理透视投影和图像扭曲时。
