目录
摘要
Abstract
文献阅读:利用物理信息神经网络模拟多物种流动和传热
文献摘要
讨论|结论
理论基础
基础方程
归一化物理方程
PINN-1
PINN-3
实验设置
网格深度和宽度对损失值的影响
同CFD模拟结果的对比
Fluent实例:管道的湍流分析
网格划分
求解器设置
结果展示
理论知识部分
总结
摘要
在本周中,通过阅读文献,了解使用PINN来对多物料的传热流动进行模拟,文章中使用传统PINN(PINN-1)和改进过的PINN-3:它使用三个网络来求解控制方程,并在训练过程中在pinn之间传输相关的解变量。通过改进MLP超参数和网格深度以及学习率后,确定了PINN的最佳范围,并与CFD结果进行比较,发现经过改进的PINN-3在模拟方面有着更好的效果。在Fluent中,选用管道湍流分析,进行几何划分和设置求解。理论学习方面,对有luent算法基本知识进行了学习。
Abstract
During the week, I read the literature on the use of PINs to simulate heat transfer flows in multiple materials, using the traditional PINN (PINN-1) and the improved PINN-3: it uses three networks to solve the governing equations and transfer the relevant solution variables between the pinns during training. By improving the MLP hyperparameters and grid depth and learning rate, the optimal range of the PINN was determined and compared with the CFD results, and the improved PINN-3 was found to have better results in simulation. In Fluent, I chose the pipe turbulence analysis to do the geometry and setup solving. In terms of theoretical learning, I learned the basic knowledge of luent algorithms.
文献阅读:利用物理信息神经网络模拟多物种流动和传热
Simulation of multi-species flow and heat transfer using physics-informed neural networks
文献摘要
本文中使用单网络和隔离网络的物理信息神经网络(PINN)架构应用于预测简单二维矩形域中干燥空气加湿问题的动量、物质和温度分布。创建的PINN模型考虑了可变流体特性、物种和热扩散以及对流。
训练模型的方法:使用不同的超参数设置训练上述两种PINN架构,以找到性能最佳的配置。结果表明,对于给定问题,单网络和隔离网格相比,隔离网络PINN方法的平均损失降低了62%。此外,单网络变体努力确保物种在计算域的不同区域的质量守恒,而分离方法成功地保持了种类的恒定。在给定的一组边界条件下,PINN预测的速度、温度和物种分布与使用OpenFOAM软件生成的结果进行了比较。单网络模型的物种质量分数的平均误差百分比为9%,隔离网络方法的平均误差百分比为1.5%。
为了展示PINN在多物种问题替代建模中的适用性,本文训练了一个参数化版本的分离网络PINN:它可以产生不同的水蒸气入口速度的结果。相对于OpenFOAM结果,在三种预测情况下,速度和温度的归一化平均绝对百分比误差约为7.5%和水蒸气质量分数的2.4%
讨论|结论
同传统的FVM方法相比,使用PINN来模拟流体问题可以实时仿真和逆建模。
PINN框架可以同时模拟多种边界条件和几何形状,而对于传统的CFD,不同的模拟必须明确配置并在多台计算机上运行,这使得代理建模成为一项昂贵的工程工作,从而降低了成本。
多组分流动和传热pinn应用的一个实际例子是开发一种气体化学反应器替代模型,该模型可用于快速模拟不同进口浓度下的产品产量。
同框架下的PINN有多个种类:
- Rao等人12提出了一种混合变量PINN方法,该方法消除了计算网络损失函数高阶导数的需要.作者发现,对于所考虑的问题,训练后的pinn可以准确地预测瞬态速度和压力分布。此外,他们表明,与传统的高阶梯度估计方法相比,所提出的混合变量方法具有更快的收敛速度,并且将初始和边界条件损失乘以2也减少了训练时间。
- Cai等13将pinn应用于求解动量和能量输运控制方程的各种传热问题。经过训练的非线性非线性神经网络能够通过推断混合对流的未知热边界条件来解决反问题。作者表明,与参考溶液相比,pinn可以准确地重现热边界条件,精度在1%以内。作者还将pin用于散热器设计优化,从而解决了前向问题,展示了该技术在工业设计优化中的应用。
- Mao等人14研究了pinn的精度,以解决由欧拉方程控制的高速流动中的正逆问题。结果表明,在L2误差为102的密度和105阶的压力和速度下,PINN模型可以准确地预测精确解和参考解。如前所述,作者还将pinn应用于反求问题,特别是从稀疏压力梯度和压力测量中推断密度、速度和压力场,复制高速气动流动通常使用的纹影实验数据处理。
- Jagtap等人15提出了一种自适应激活函数,旨在加快PINN训练的收敛速度。作者表明,与深度学习中使用的传统常数激活函数相比,将自适应函数应用于Klein-Gordan、非线性Burger和Helmholtz方程的建模可以产生更快的收敛速度。
- Meng等人16提出了一种拟实PINN方法,该方法将问题分解为许多短时间集成网络。作者将提出的技术应用于一维Burgers方程问题和二维反应扩散问题,在PINN训练过程中显示出显著的收敛时间改善。
在本工作中,将探讨pinns同时求解稳态动量、物种和能量方程的准确性。将实现两种PINN建模方法:第一种是典型的方法,使用单个网络来解决所有物理问题,并将其称为PINN-1方法。第二种方法称为PINN-3,它使用三个网络来求解控制方程,并在训练过程中在pinn之间传输相关的解变量。
以简单的二维干空气加湿风道流动问题为例,将PINN结果与CFD模拟结果进行对比。此外,还进行了超参数搜索,比较了不同深度和宽度神经网络的PINN-1和PINN-3方法的损失值。在当前的工作中,使用PyTorch19库来创建和训练各种pinn。
结果表明,几乎在所有情况下,与由此产生的PINN-1损失相比,PINN-3方法产生的损失值更低。平均而言,对于所有训练的模型,PINN-3损失比PINN-1值低62%。
单网络方法可以充分解决动量和能量偏微分方程,但难以满足物种质量输运要求,而PINN-3方法则成功解决了物理偏微分方程。减少模型建立时间的一种可能的方法是使用两个网络,一个用于动量和能量,另一个用于物种质量分数预测。
与分离变体相比,PINN-1模型架构性能的平均下降可归因于这样一个事实,即PINN-1模型的组合损失函数采用更复杂的形式,因为它依赖于所有剩余和边界条件损失函数(质量,动量,物料,能量和通量项)。这导致了不同的原因,为什么单一网络方法可能导致更高的损失。
其中一个可能是:对于PINN-1体系结构,与从单个组合损失函数计算的其他梯度相比,某些误差、权重值更大。梯度的差异导致训练偏向于忽略某些残差和边界损失函数,这导致Wang等人提到的欠拟合和延长训练时间。
相反,在隔离架构的情况下,不同物理之间的梯度更新机制是分离的,因为三个网络实现了三个独立和顺序的优化器。此外,三个pinn的单个组合损失值也依赖于较少的内部损失,从而简化了单个网络需要学习的传递函数。一种解决方案是在训练过程中应用主动损失加权。
PINN-3方法还应用于开发替代模型,其中水蒸气入口速度边界条件是一个额外的网络输入。分离的PINN方法可以充分预测不同入口速度下的速度、温度和水质量分数分布,展示了建立参数化模型的能力。
理论基础
基础方程
为了解决整个区域中质量、动量、物质和能量的层流稳态输运,需要同时解决以下偏微分方程:
质量方程:

动量方程:
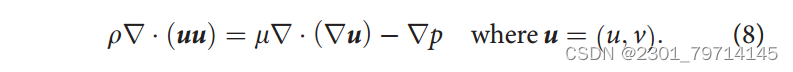
物料方程:

能量方程:

归一化物理方程
归一化输入和解变量定义为:

带星号的为无量纲变量,所选内坐标由pinn解出的方程为:
质量方程:
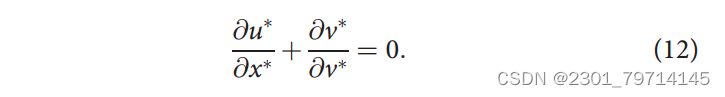
动量方程:

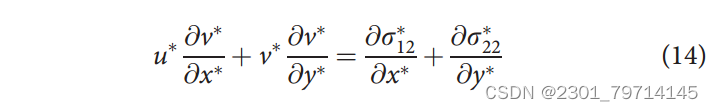
其中:
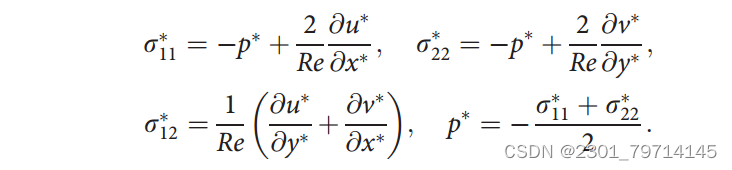
物料方程:

其中:

能量方程:

为了确保学习到的网络参数在计算域中执行物理方程,需要最小化单个残余损失值:
要计算剩余损耗值,需要将上述归一化方程的所有量都写在等号的一侧,然后对域中所有i个内部点取平方平均值。例如,x动量和i种输运方程的剩余损失计算为:
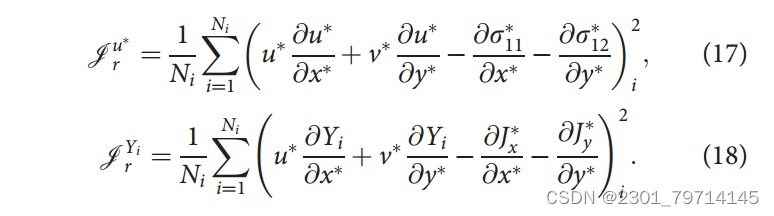
残余损失值仅在内部点处强制执行,而不在边界边缘处强制执行。因此,在找到解决方案之前,需要关闭边界。通过定义边界损失函数来实现的,与在网络训练期间最小化残差损失类似。最小化边界损失函数将确保施加各种进口,出口和壁面边界条件。边界损失函数的估计需要计算边界边缘的解变量,并将计算值强制为所需的边界条件值,进口边界速度损失如下:
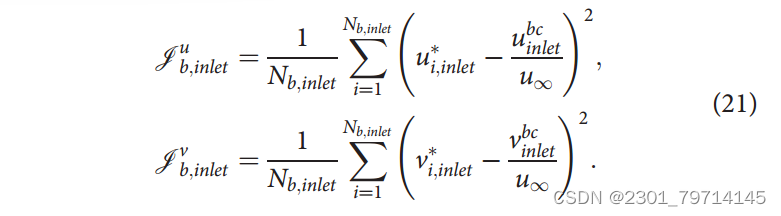
PINN-1
图2显示了PINN-1模型的示意图,并概述了计算量。PINN-1布局是典型的PINN配置:

PINN-1使用单个优化程序进行训练,以同时解决所有物理方程。在本工作中,MLP网络接受X星号和Y星号的值并输出18个物理量。在各个边界和内部点处评估的这18个量然后用于计算综合损失值。在网络参数的训练过程中,使用每次训练迭代开始时预测的温度和物种组成来更新每个内部点的流体性质,更新的流体性质与预测的物理量一起用于估计损失值。
PINN-3
图3显示了PINN-3配置的示意图。从示意图中可以看出,归一化的空间坐标被馈送到三个MLP网络,然后预测各种物理量:

灵感来源于FVM中线性方程组的传统多解方法。例如,在FVM中,压力场用GAMG求解,速度场用预条件双共轭梯度求解器求解,温度场和物种场用高斯-赛德尔光滑求解器求解。
对于PINN-3方法,与PINN-1模型类似,使用每个MLP网络的预测值来计算pinn的残差和边界条件损失。然后使用损失来更新每个MLP网络的权重和偏差。对每个网络执行自动微分,以计算网络特定组合损失相对于该网络的可训练参数的梯度。然后使用三个损失梯度集和三个Adam优化器分别更新每个网络的权重和偏差。
一些预测变量在pinn之间直接或间接共享。这些预测量在网络之间的传输需要计算每个pin网络的剩余损耗。例如,将预测的归一化速度输入到物种和能量输运pinn的剩余损失计算块中,以计算pde的对流量,,域中每个内部点的温度和成分被发送给流体性质函数,然后该函数将密度场返回给每个网络。比热容又由流体性质函数返回到能量PINN。PINN-3方法的训练策略包含了预测物理量的网络间共享。
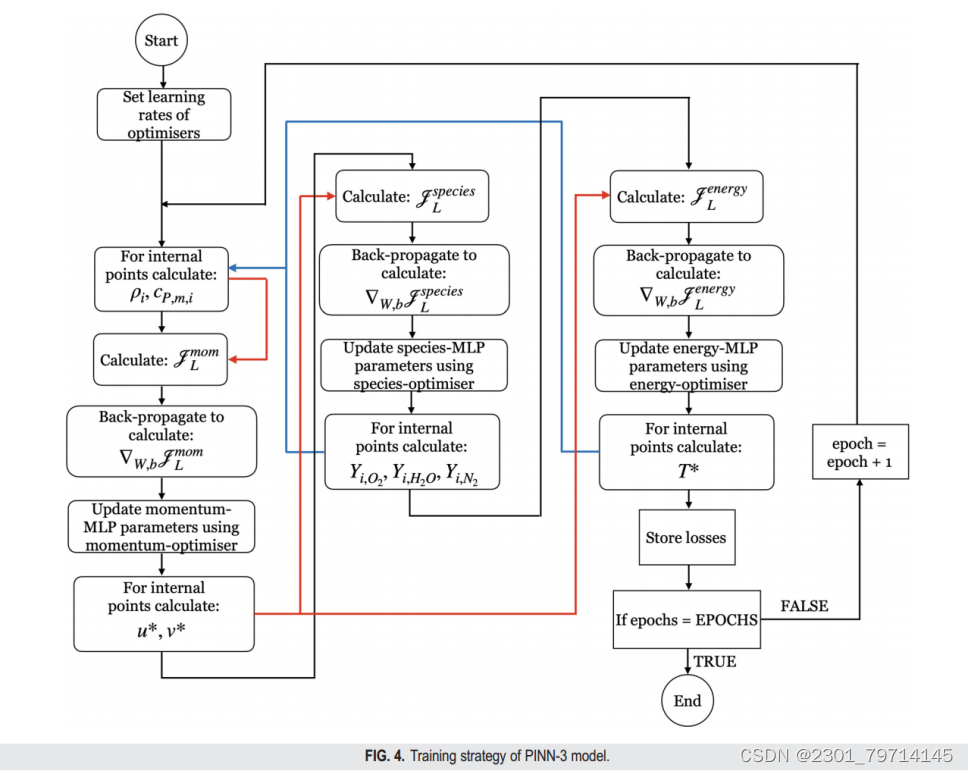
图4显示了训练策略的流程图。训练策略首先指定三个Adam优化器的学习率,并初始化域内每个内部点的可变流体属性。对于前100次训练迭代,使用300 K的干燥空气成分作为输入,保持流体特性不变。在前100次迭代之后,每个训练周期都会使用不同的内部点温度和物种组成来更新流体特性。一旦计算出流体性质并将其传递给相应的PINN实例,就可以计算出质量和动量PINN组合损失以及MLP参数损失梯度。通过质量和动量PINN的Adam优化器应用参数梯度来更新权重和偏差。一旦更新,质量和动量的PINN被用来计算归一化(其余两个方程同理):
实验设置
所考虑的域是尺寸为0.5 ×0.1 m2的简单二维矩形笛卡尔域,如图1所示,该域具有干空气入口(inlet)、混合物出口(outlet)、水蒸气入口(bot wall)和恒温固体壁(top wall):
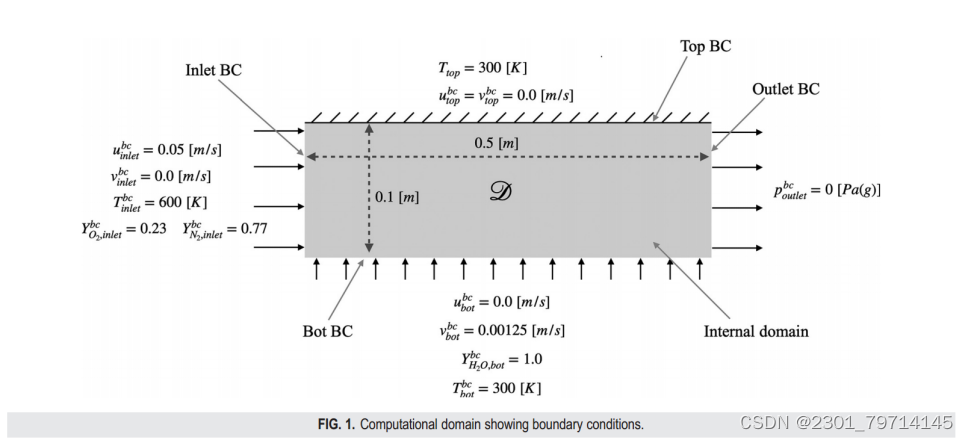
在训练过程中,所有这些边界值都保持不变,而未提及的变量,如压力,则是由PINN在进口边界处求解的结果。由于顶壁是一个不可穿透的边界,穿过的流量为0;因此,边界质量分数不指定,是由神经网络计算的结果。在出口边界处,pbc出口为出口压力边界条件,出口其他变量均为神经网络计算的结果。
密度场和相关输运方程是在假定流体混合物是不可压缩理想气体的情况下求解的,因此密度仅是局部气体温度和混合物成分的函数。
网格深度和宽度对损失值的影响
进行了粗网格搜索,其中每个隐藏层的神经元数量、隐藏层的数量和D域中的采样点数量是不同的。测试的不同超参数如表1所示:

每隐层51个神经元的PINN-1模型(包含5个隐层)具有8823个可训练权参数,每隐层30个神经元的PINN-3模型具有3个,最终结果在25000次之后得到,学习率为5×10-3 (5000)、1×10-3(10000)、1×10-4(10000)次迭代,对于给定的设置,每个网络训练三次,并报告平均结果。
图5显示了动量、种类和能量损失(PINN-1 )的平均训练历史:

可以看出,除了51个神经元的PINN-1模型的物种和能量损失与30个神经元的PINN-3模型的损失值相似外,PINN-3模型在所有情况下都比PINN-1方法产生更低的损失。对所有训练案例进行平均,与各自的PINN-1损失相比,PINN-3模型的动量降低82%,能量降低87%,物种损失降低94%,最佳的PINN-3设置是每个隐藏层50个神经元,而对于PINN-1模型,86个神经元为最佳。
利用上述最佳神经元数量设置,通过增加隐藏层数对模型进行再训练,研究MLP网络深度对综合损失值的影响,通常,更深的网络需要更多的训练时间来收敛;将训练计划调整为:5×10-3(5000);1×10-3(20000);1×10-4(20000);1×10-5(20000);1×10-6(20000);
图6显示了不同深度MLP网络的训练历史。结果再次表明,与PINN-1模型的结果相比,PINN-3模型在动量、物种和能量预测方面的损失更低。在动量、能量和物种损失值上,PINN模型之间的平均百分比差异分别为68%、78%和86%。7层PINN-3模型的物种和能量损失最低,5层模型的动量损失最低:

通常,较深的网络和较高的采样密度,理论上应该比较浅的模型和较低的采样密度产生更低的损失,给定足够的训练周期。在当前的工作中,正如稍后将展示的那样,本节中发现的最佳性能设置生成的结果具有足够的精度,可以捕获物理偏微分方程的解。图7显示了使用更高采样密度训练的PINN-1和PINN-3模型的综合损失值。
图表显示,使用15,000个采样点训练的PINN-3模型优于更高采样密度的模型。对于PINN-1模型,以3万个坐标点训练效果最好。尽管在3万个训练点下,PINN-3模型的综合损失值要高于1.5万个训练点,但是直接与of结果相比,它的预测结果更加准确。
图7显示了使用更高采样密度训练的PINN-1 (5、86)和PINN-3 (5、50)模型的综合损失值:

图表显示,使用15,000个采样点训练的PINN-3模型优于更高采样密度的模型。对于PINN-1模型,以3万个坐标点训练效果最好。
同CFD模拟结果的对比
图8显示了OF和PINN模拟模型生成的预测X和y速度结果:
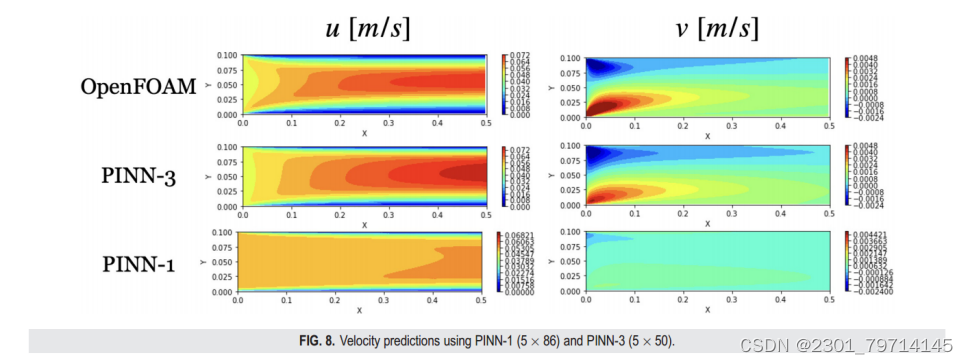
Pinn3和OF结果吻合良好。相反,与OF结果相比,可以看到PINN-1模型对x速度值的预测明显不足。此外,它还低估了区域下半部分的y速度,而高估了靠近顶壁的y速度。从PINN-1速度的结果可以看出,该模型在速度梯度较大的区域表现不佳。
图9显示了预测的温度和物种质量分数分布。PINN-3的预测再次与OF的结果非常吻合。PINN-1模式预测的平均温度场较低,不能准确预测底壁附近形成的水浓度边界层。图9还显示了对内部域的总和质量分数的预测。如图所示,PINN-3模型的结果都接近期望值1,而PINN-1方法则难以实现损失条件。如前所述,PINN-1模型无法捕获所需物理特性的一个可能原因可能是,由于只使用单个网络,因此在训练期间只有一个组合损失值被最小化。这导致只有某些方面的偏微分方程的最小化:
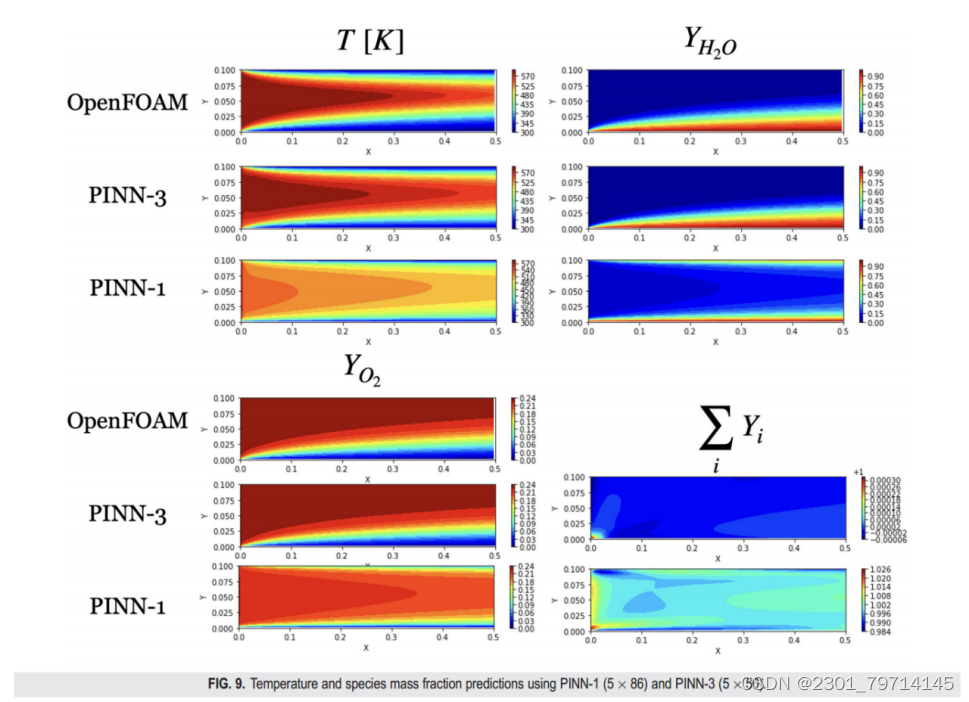
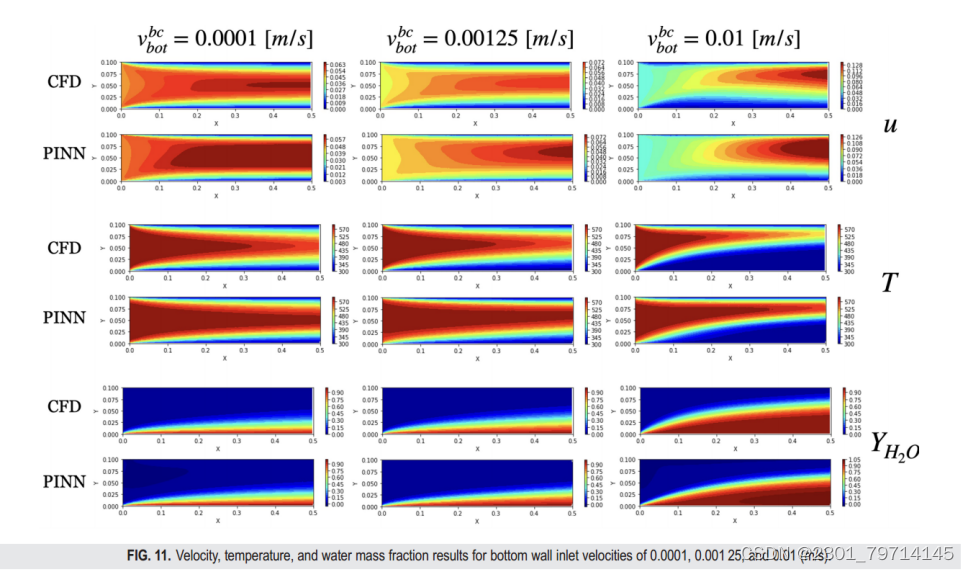
图11显示了x速度、温度和H2O质量分数的PINN-3和OF预测。结果表明,PINN-3模型能够较准确地捕捉水汽注入速度增大时的速度和温度分布。值得注意的是,与of模型的结果相比,PINN模型预测的管道中心附近的x速度更高,这导致热进口流体(600 K)更深地渗透到管道中。PINN可以相对准确地捕捉到底部壁面附近水汽质量浓度边界层随着速度的增加而增长的过程,显示了其捕捉扩散力和对流力的能力:
Fluent实例:管道的湍流分析
网格划分
由于本次案例使用的是现有模型,故针对网格问题进行进一步调整:

放大发现,网格并没有完成覆盖,会影响计算的过程和准度,要对其进行划分调整:

先将其Cylinder划分出来,进行单个的网格划分,提升Cylinder内的网格精度,与管道控制体结合起来发现,其边界不明确,故对Cylinder的边加设一次尺寸调整和网格划分:

调整过后如下图:

求解器设置
进入Fluent求解器设置,选用k-epsilon模型,采用壁面函数法进行求解运算,数据保持默认选择,选择管道中流体为水,可对对应参数进行调整,具体问题具体分析,把固体材料设置为铝材,设定入口出口的湍流强度和回流湍流强度,可用下式计算,经计算得入流湍流强度为4.51%:
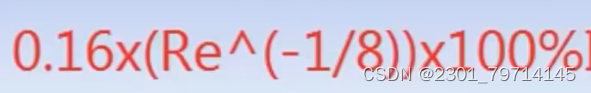
使用满流情况进行模拟,其具体参数如下:

 求解方式选择为SIMPLE,都采用二阶逆流方式进行湍流模拟,进行1000次迭代后,各参数如下曲线图表示:
求解方式选择为SIMPLE,都采用二阶逆流方式进行湍流模拟,进行1000次迭代后,各参数如下曲线图表示:
结果展示
压力场:

速度场:
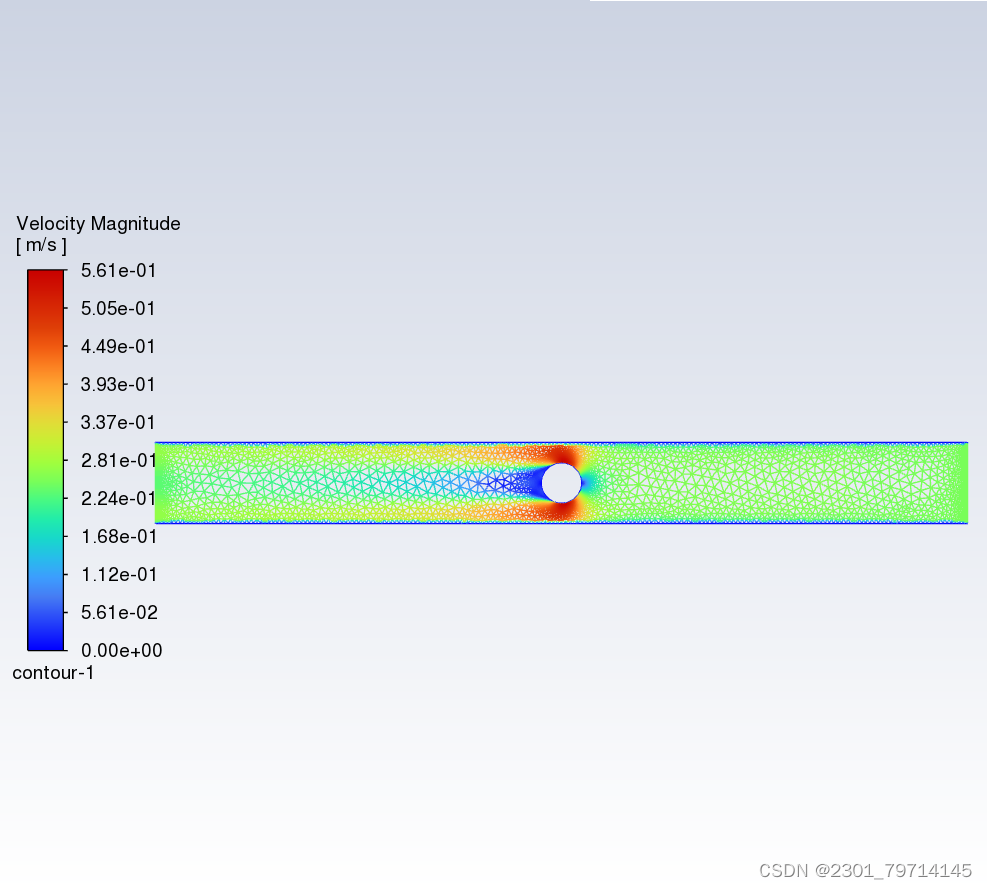
湍流动能:

理论知识部分





总结
本周通过学习Fluent相关的算法,巩固了软件的理解和使用,能更好的理解在什么情况下设置正确的边界条件和如何采取正确的求解方法来进行仿真。阅读文献时会更关注其创新点和实验方式,为了以后的写作中提供更多的灵感。
