企业网组建_深圳正规网站建设服务_新站如何快速收录_精准客源引流平台

本篇博客详细讲解一下离散化知识点，通过讲解和详细列题带大家掌握离散化。

题目：

原题链接：https://www.acwing.com/problem/content/description/804/

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。
现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。
接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式
第一行包含两个整数 n 和 m。
接下来 n 行，每行包含两个整数 x 和 c。
再接下来 m 行，每行包含两个整数 l 和 r。

输出格式
共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围
$-10^9\le x\le 10^9$,
$1\le n,m\le 10^5$,
$-10^9\le l\le r\le 10^9$,
$-10000\le c\le 10000$

输入样例：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例：

8
0
5

什么是前缀和？（会此算法可以跳过不看）

一维前缀和&一维差分（下篇讲解二维前缀和&二维差分）（超详细，python版，其他语言也很轻松能看懂）

什么是离散化？

   本题猛的一看似乎就是一道前缀和的模板题，但需要注意到这里所谓的“坐标”的范围较大，范围在$-10^9\le x\le 10^9$,为了存下被修改的点的数据，如果将它们的坐标作为数组的下标就需要开一个$2\ast 10^9$大小的数组，肯定会爆内存，况且这里的坐标还有负值，不方便进行存储。

   所以要提出一个新的能方便快捷存数据的算法——离散化。

   离散化的内存优化思路是只存储那些被用到的点（在这里指的是“被加了值的点”以及“要查询区间的两个端点”），然后利用一些较小的值来代替它们的坐标进行索引，并最终保持它们的相对位置。

   举个例子：对于“被用到的点”只有四个：1、11、886、320001，如果用传统的存储方式要开1～320001个连续的存储空间，但其实没必要，因为会浪费掉了很多没有用到的空间。其实它们的相对位置可以分别用1（1）、2（11）、3（886）、4（320001）来替代，进而只需要开1～4个连续的存储空间并且全部用上；反观此题的数据量，操作次数决定要存点的个数，n、m均小于等于$10^5$，所以“被用到的点”最多为$n+2m=3\ast 10^5$个 ，也即内存从$2\ast 10^9$优化到了$3\ast 10^5$，整整少了4个数量级！

   因此，点的存储位置变为连续，但其表示的值却为离散，故而称其被离散化。

如何离散化？（题解）

   为了能够将较大的坐标点及其该坐标点上的数值存储下来，就需要使用两个映射：

1. total_num（数组）：用来存放题目中用到的坐标点，也就是题中的x, l, r，初始值为空数组。total_num数组表示坐标到相对位置的映射：先将题目中输入样例给出的坐标点全都放入（append）total_num数组后，进行一遍排序和去重，这样就必能保证小的坐标位置在前，大坐标在后，此时下标就是它们新的“相对位置”。
2. a（数组）：用来存放离散化后的坐标的值的变化，初始范围为$3\ast 10^5+10$ (n + 2m 最大为$3\ast 10^5$)。表示相对位置到坐标点上的数值的映射：拿到坐标点的相对位置new_x后，a[new_x] += c就存下了坐标点的数据了。

   这里还需要定义add_num数组用来存放整数(x, c)，定义query_num数组，用来存放询问的区间(l, r)

   再定义a的前缀和数组s，预处理完后利用s[r] - s[l - 1]就能得到 [l,r] 区间和了。

   下面来详细讲解一下各数组的作用和具体实现方法：

   首先初始化各个数组，其中a数组和s数组的长度为 $3\ast 10^5+10$，值为0，其余数组初始为空。

   total_num数组为何除了要存被改动点的坐标x还要存储查询区间的两端点l和r呢？

   主要是因为后续要通过s[r] - s[l - 1]来获取到区间和，而必须将它们在坐标轴上的情况也存下来才能知道这个区间的情况，因而它也算作“被用到的点”。

   那么被改动点（x, c）和查询端点（l, r）分别还要再放到add_num和query_num里方便处理。

   具体的存储情况还可以下图为例：

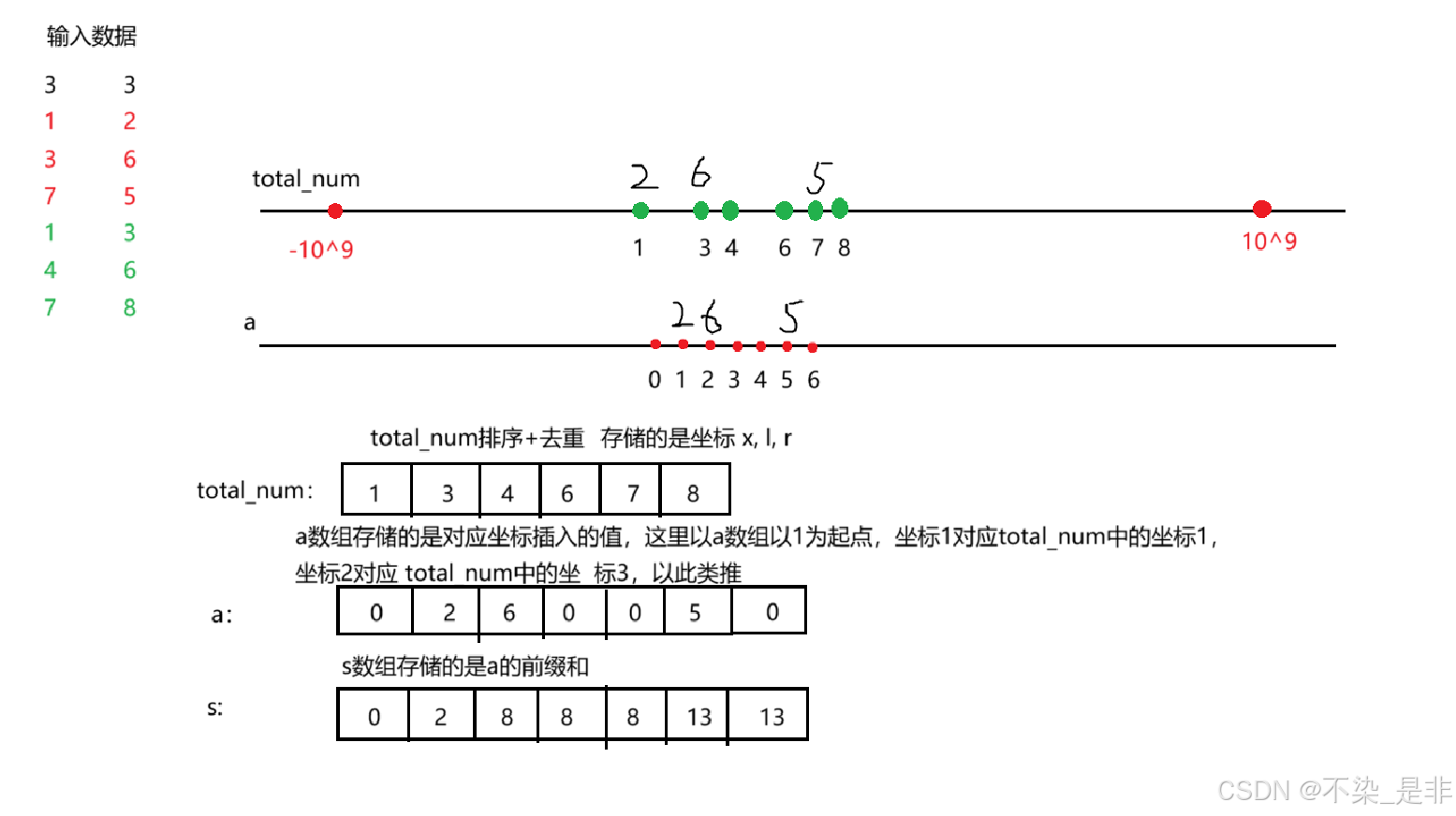
   这里还有一个难点就是如何进行离散化？也就是如何把total_num数组映射到a数组上？这里需要借用二分来进行插入操作，二分的初始左端点 l 为0，右端点 r 为total_num数组的长度减一，mid = (l+r) // 2，传入参数是x(这里的x是toal_num里的数值，需要对total_num进行遍历并挨个把total_num中的值映射到a数组中)，只要total_num[mid] <= x，那么r = mid 否则 l = mid + 1，最后返回值是 l + 1。

   为什么返回的是 l + 1 呢？因为a数组和s数组的下标是从1开始的（下标从1开始是方便处理前缀和），所以这里需要进行+1操作。

   下面给出详细代码和注释：

# 读取输入的n和m，分别表示添加操作的数量和查询操作的数量  
n, m = map(int, input().split())  
N = 300010  
a = [0] * N  
s = [0] * N  
# 用于存储添加操作的列表，每个元素是一个元组，包含要添加的数值x和对应的增量c  
add_num = []  
# 用于存储查询操作的列表，每个元素是一个元组，包含查询的区间左端点l和右端点r  
query_num = []  
# 用于存储所有出现过的坐标
total_num = []  # 读取n个添加操作  
for i in range(n):  x, c = map(int, input().split())  add_num.append((x, c))  total_num.append(x)  # 将x添加到total_num中  # 读取m个查询操作  
for i in range(m):  l, r = map(int, input().split())  query_num.append((l, r))  total_num.append(l)  # 将l添加到total_num中  total_num.append(r)  # 将r添加到total_num中  # 对total_num进行排序并去重，得到所有唯一出现过的数值  
total_num = list(set(sorted(total_num)))  # 定义一个查找函数，用于在total_num中找到数值x映射到a的位置（索引从1开始）  
def find(x):  l = 0  r = len(total_num) - 1  while l < r:  mid = (l + r) // 2  if total_num[mid] >= x:  r = mid  else:  l = mid + 1  return l + 1# 对每个添加操作进行处理，将增量c添加到对应的位置  
for x, c in add_num:  new_x = find(x)  # 找到total_num中x映射到a的位置a[new_x] += c    # 将增量c添加到a数组的对应位置  # 计算前缀和数组s  
for i in range(1, N):  s[i] = s[i - 1] + a[i]  # 前缀和公式# 对每个查询操作进行处理，计算并输出区间和  
for l, r in query_num:  xl = find(l)  xr = find(r)  print(s[xr] - s[xl - 1])