#### 网络各层安全协议
链路层:链路隧道协议、加密技术
网络层:包过滤机制、NAT、IPsec协议、 VPN
传输层/会话层 :SSL/TLS 协议
应用层:SHTTP、HTTPS、PGP、S/MIME等
### 网络安全技术
第二代安全技术
- 保护
- 响应
- 检测
- 恢复
包括
- 防火墙
- 入侵检测
- 虚拟专用网
- 公钥基础设施
# 密码学
### 发展进程
- **古典密码**: 基于字符替换的密码,现在已很少使用了,但是 它代表了密码的起源
- **对称密钥体制( Symmetric System** ):加密密钥和解密密钥 相同,这些算法也叫作单钥密码体制(one-key system)
- **非对称密钥体制(Asymmetric System)** :加密密钥和解密密 钥不同,也叫**公钥密码体制(public key system)或双钥密码体制(two-key system)**
### 加密模式
- **序列密码(stream cipher)**: 序列密码**按位或字节加密**,也 可以称为流密码,序列密码是手工和机械密码时代的主流。
- **分组密码(block cipher)**: 分组密码**将明文分成固定长度的组**,用同一密钥和算法对每一块加密,**输出也是固定长度的密文**。
## 对称密码
### DES(数据加密标准,Data Encryption Standard )
DES是一种对二元数据进行加密的算法,数据分组长度为 **64位**,密文分组长度也是**64位**,使用的密钥为**64位**,有效密钥长度为**56位**,**有8位用于奇偶校验**,解密时的过程和加密时相似,但密钥的顺序正好相反,DES的整个体制是公开的,系统的安全性**完全靠密钥的保密**。
## 对加密系统的攻击
- 唯密文攻击:根据加解密算法和密文进行破译
- 已知明文攻击:攻击者拥有部分密文和对应的明文,根据算法寻找密钥
- 选择明文攻击:有选择地使用任意明文和与之对应的密文信息,根据算法寻找密钥
- 选择密文攻击:有选择地使用密文和与之对应的明文信息,根据算法寻找密钥
## 分组密码
分组密码一次处理一个数据分组
对于较长的明文,在分解成若干个分组之 后,采用相同的密钥进行加密,NIST定义 了5种工作模式
- **电码本ECB(Electronic Codebook)**
- **密码分组反馈CBC(Cipher-block chaining)**
- **密码反馈CFB(Cipher feedback)**
- **输出反馈OFB(Output Feedback)**
- **计数器CRT(Counter)**
## 公钥密码
### RSA
#### 过程
##### 密钥生成
1. **选择两个互异的素数p和q**
2. **计算n=p*q**
3. **计算φ(n)=(p-1)(q-1)**
4. **选择与φ(n)互素的e,且1<e<φ(n)**
5. **计算d*e mod φ(n)= 1 **
**公钥为Pk为{e,n},私钥为{d,n}**
**加密**
$$
C=M^e\,(mod\,n)
$$
**解密**
$$
M=C^d\,(mod\,n)
$$
### ELGamal密码
- todo
# 消息认证与身份认证
数字签名-消息的不可否认性
消息认证-消息的完整性
### 数字签名
#### 基本概念
① 签名者事后不能抵赖自己的签名;
② 任何其他人不能伪造签名;
③ 如果当事的双方关于签名的真伪发生争执,能够在公正的仲裁者面前通过验证确认其真伪。
#### 与加解密的区别
数字签名的加密/解密过程和信息(报文)的加密/解密 过程都可适用公开秘钥算法,但实现**过程正好相反**,适用的密钥对也不同。数字签名使用的是发送方的密钥对, 发送方用自己的私钥进行加密(签名),接收方用发送方的公开秘钥进行解密(验证)
这是一个一对多的关系:任何拥有发送方公开秘钥的人都可以验证数字签名的正确性
签名
设施加签名的算法为 SIG,产生签名的密钥为K,被签 名的数据为M,产生的签名信息为S
$$
S = SIG (M,K)
$$
验证签名的算法为VER ,用VER对签名S进行验证,可鉴别S的真假
$$
VER(S, K)=
\begin{cases}
true \quad当S=SIG(M, K)\\
false \enspace当S\neq SIG(M, K)
\end{cases}
$$
#### 公钥实现数字签名
1. **A用自己的解密钥K~dA~对数据M进行签名:S~A~=D(M,K~dA~)**
2. **如果不需要保密,则A直接将S~A~发送给用户B**
3. **如果需要保密,则A用B的公开的加密钥K~eB~对S~A~ 加密, 得到密文C,其中C=E(S~A~,k~eB~)**
4. **最后,A把C发送给B,并将S~A~或C 留底**
5. **B收到后,若是不保密通信,则用 A的公开加密钥K~eA~对签名进行验证**
$$
E(S_A,K_{eA})=E(D(M,K_{dA}),K_{eA})=M
$$
6. **若是保密通信,则 B先用自己的保密的解密钥K~dB~对C解密, 然后再用A的公开加密钥K~eA~对签名进行验证**
$$
D(C,K_{dB})=D(E(S_A,K_{eB}),K_{dB})= S_A \\
E(S_A,K_{eA})=E(D(M,K_{dA}),K_{eA})= M
$$
7. **M如果能够恢复出正确的 M,则说明S~A~是A的签名,否则SA不是A的签名**
8. **B对收到的 C或S~A~留底**
分析
因为只有 A才拥有K~dA~ ,而且由公开的K~eA~在计算上不 能求出保密的解密钥K~dA~ 。因此签名的操作只有A才能进行,任何其他人都不能进行。所以,K~dA~就相当于A的印章或指纹,而SA就是A对M的签名。对此A不能抵赖,任何其他人不能伪造
##### 合理设计明文的数据格式



##### RSA签名
设 M 为明文 , K~eA~= 是 A 的公开加密钥 , K~dA~=是A的保密的解密钥,则A对M的签名过程是
$$
S_A=D(M,K_{dA})=M^d(mod\;n)
$$
S~A~便是签名
验证
$$
M=E(S_A,K_{eA})=(M^d)^emod\;n
$$
#### 盲签名
**需要 某个人对某数据签名,而又不能让他知道数据的内容。称这种签名为盲签名( Blind Signature)**

双联签名
双联签名是实现盲签名的一种变通方法。它利用协议和 密码将消息与人关联起来而并不需要知道消息的内容。从 而实现盲签名
双联签名采用单向HASH函数和数字签名技术相结合, 实现盲签名的两个特性
#### 作业
1.为什么数字签名能够确保数据真实性?
因为只有 A才拥有K~dA~,而且由公开的K~eA~在计算上不能求出保密的解密钥K~dA~ 。因此签名的操作只有A才能进行,任何其他人都不能进行。所以,K~dA~就相当于A的印章或指纹,而S~A~就是A对M的签名。对此A不能抵赖,任何其他人不能伪造
2.说明对于RSA的数字签名,为什么先加密后签名不安全?
1. 容易受到重放攻击。攻击者可以截获密文并重复发送,因为签名是对加密数据的签名,而不是对明文的签名。
2. 容易受到中间人攻击。攻击者可以截获密文,然后用自己的密钥对密文重新签名,然后将签名后的密文发送给接收者。接收者无法检查签名是否来自合法的发送者,因为签名是对整个消息(包括加密的数据和签名)进行的。
3.说明HASH函数在数字签名中的作用。
Hash函数在数字签名中应用的意义是为了增加可识别信息。在数字签名中,对消息进行Hash的作用是将**任意长度的消息压缩成固定长度的消息指纹**。同时提供完整性
4. 盲签名与普通签名有何不同?举出一个盲签名的实例。
盲签名是一种数字签名技术,可以让一个签名者在不知道签名信息内容的情况下,对这个信息进行签名,从而保护用户的隐私
实例:电子商务和电子政务
5. 举出一个双联盲签名的实例
```
双联盲签名是一种密码学协议,用于在保护用户隐私的同时进行数字签名。这里给出一个基于椭圆曲线加密算法(Elliptic Curve Cryptography)实现的双联盲签名示例:
假设有两个参与者Alice和Bob,他们想要对某条消息m进行双联盲签名。
1. Alice选择一个随机数r1,并计算R = r1 * G,其中G为预定义的生成点。
2. Bob也选择一个随机数r2,并计算S = r2 * G。
3. Alice将R发送给Bob,而Bob则将S发送给Alice。
4. Alice使用自己持有的私钥a来计算T = R + a*H(m),其中H()表示哈希函数应用到消息m上得到结果h。然后她将T返回给Bob。
5. Bob同样使用自己持有的私钥b来计算U = S + b*H(m)并返回给Alice。
至此,在不泄露彼此信息以及原始消息内容情况下完成了“双”、“联”、“盲”的过程。
最后, 通过以下方式验证该签名:
- 验证步骤:检查 T ?= U
如果相等,则说明该数字签名有效且匿 名性质满足条件。
```
- 签名算法利用私钥生成签名,称消息m的签名为sig(m),然后将(m,sig(m))发给接收方
- 验证算法利用签名者的公钥对sig(m)进行解密,如果解密输出与m一致,则为合法数据。
由于无法识别数字签名与其拷贝之间的差异,所以, 在数字签名前应加上时间戳
### 消息认证
- 加密函数
- 消息认证码MAC
- 散列函数
散列函数
- **抗原像攻击(单项):给任意的h,找到H(x)=h在计算上不可行**
- **抗弱碰撞:给任意的x,找到y!=x 满足H(x)=H(y)在计算上不可行**
- **抗强碰撞:找到任意的满足H(x)=H(y)的偶对(x,y)在计算上不可行**
应用
- 消息认证 确保消息没有被修改、插入、删除或重放确保消息发送方声称的身份真实有效
- 文件完整性校验
- 数字签名保护消息完整性,验证消息发送方身份
- 单向口令
- 入侵检测与病毒检测
- 区块链
**保障多种安全的方案**
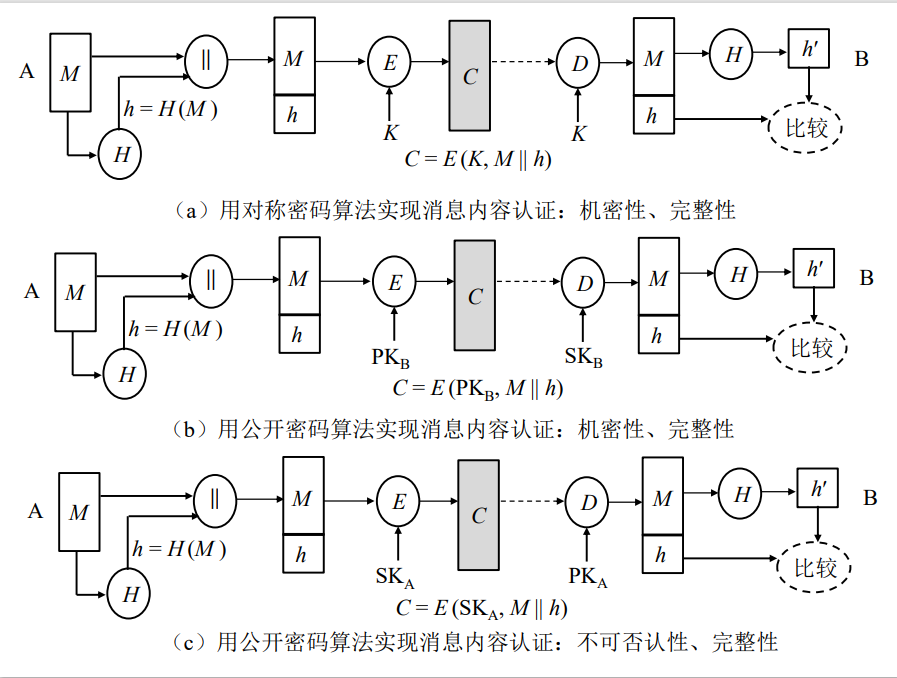
**只保证完整性的方案**
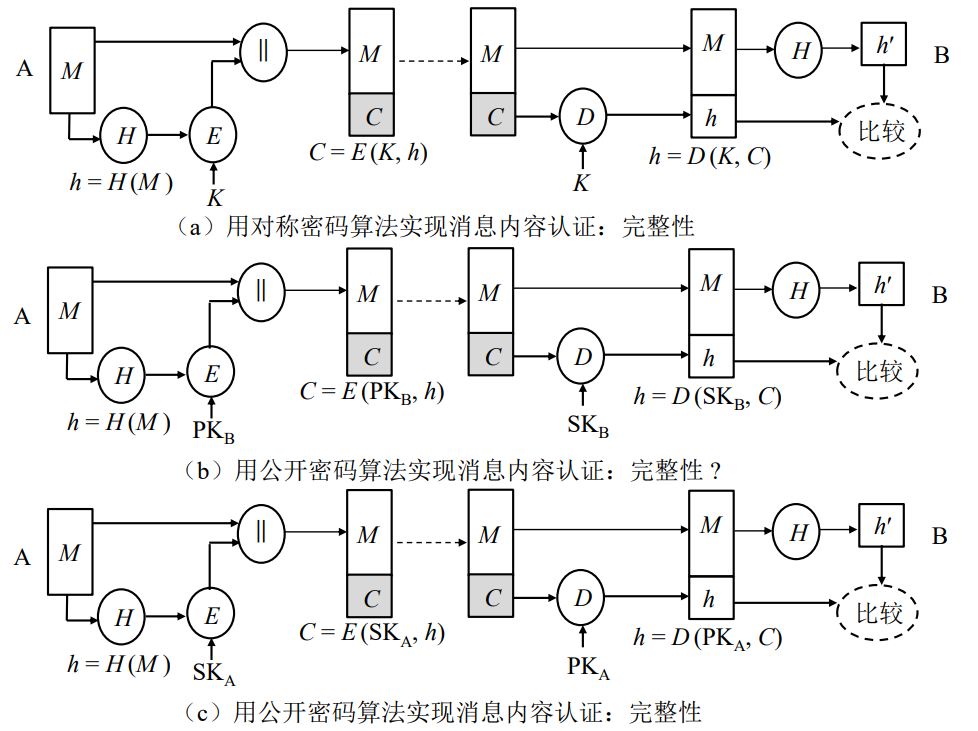
MAC
消息认证码(Message Authentication Code, MAC):通信双方需要**共享一个密钥,以K来表示**。同时,需要用于生成消息认证码的函数F。对于消息M,其消息认证码 MAC~M~与M和K相关,可以表示为:
$$
MAC_M=F(M,K)
$$
不管消息的长短,都生成固定大小的数据块
