调整 （Adjusted
）概念及详细解释
调整 是回归分析中的一个指标，用于评估回归模型的拟合优度。与标准
不同，调整
引入了对模型复杂度的惩罚，以避免因加入过多变量而导致的虚高拟合效果。
1. 标准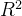 
标准 （决定系数）定义为：
其中：
- SSR 是残差平方和（Sum of Squares for Residuals），衡量模型未能解释的误差；
- SST 是总平方和（Total Sum of Squares），衡量数据的总变异性；
表示模型解释的变异比例。
问题：标准 随着模型中自变量数量的增加而单调不减，甚至当增加的变量对解释力无贡献时，
也可能上升，容易导致过拟合。
2. 调整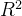
调整 修正了标准
的缺陷，通过引入模型自由度（自变量数量）对
进行调整，使得它对模型复杂度更敏感：
等价于：
其中：
- n 是样本数量；
- k 是自变量数量；
- n−k−1 是自由度。
解释：
- 调整
- 当 k 增加（自变量数量增多）时，调整
3. 性质与特点
- 范围：调整
- 变量筛选：调整
- 模型比较：对于不同的回归模型，调整
4. 优缺点
优点
- 避免过拟合：通过对模型复杂度的惩罚，有效避免过拟合问题。
- 公平比较：可比较不同复杂度的模型拟合效果。
缺点
- 灵敏度：对样本数量和自变量数量非常敏感，样本量不足时，调整
- 解释性：尽管调整
5. 调整 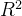的应用场景
- 变量选择：用于衡量新增变量是否显著提高模型解释力。
- 模型评价：比较多个回归模型的拟合效果，选择调整
- 模型简化：评估减少变量后的模型是否依然具有良好的拟合性能。
6. Python 示例代码
以下代码展示如何计算标准 和调整
：
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score# 示例数据
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([1.1, 2.0, 2.9, 4.1, 5.1])# 回归模型
model = LinearRegression()
model.fit(X, y)# 标准 R^2
r2 = r2_score(y, model.predict(X))# 样本数和自变量数
n = len(y) # 样本数
k = X.shape[1] # 自变量数# 调整 R^2
adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - k - 1)print(f"标准 R^2: {r2:.4f}")
print(f"调整 R^2: {adjusted_r2:.4f}")
输出结果
标准 R^2: 0.9970
调整 R^2: 0.99607. 总结
调整 是回归模型评估中的重要指标，能够平衡模型的拟合优度和复杂度。通过引入惩罚项，它在选择最优模型时尤为有效。与标准
相比，调整
更适合多变量回归分析，并能帮助我们避免过拟合风险。