
摘要
本文研究了基于模拟退火算法(Simulated Annealing, SA)的多车型车辆路径问题(Heterogeneous Fleet Vehicle Routing Problem, HFVRP)求解方法。HFVRP 是一种复杂的组合优化问题,其目标是在满足客户需求的前提下,通过合理选择车辆类型及路径来最小化总成本。
模拟退火算法通过模拟物理退火过程,逐步接近最优解,具有跳出局部最优的能力。实验结果表明,SA 能有效优化 HFVRP 的路径规划,显著降低物流成本。
理论
多车型车辆路径问题(HFVRP)是车辆路径问题的扩展版,涉及不同类型的车辆,且各类车辆的容量、成本等约束条件不同。HFVRP 的目标是最小化车辆的总运输成本,包括行驶距离和车辆选择成本。
模拟退火算法是一种基于蒙特卡洛方法的全局优化算法,通过设置初始温度,逐步降低温度,随机生成新的解并接受或拒绝,最终收敛到最优解。该算法能够避免陷入局部最优,适用于求解 HFVRP 等复杂优化问题。
实验结果
实验在随机生成的多车型路径规划实例中进行了验证,实验结果如下:
-
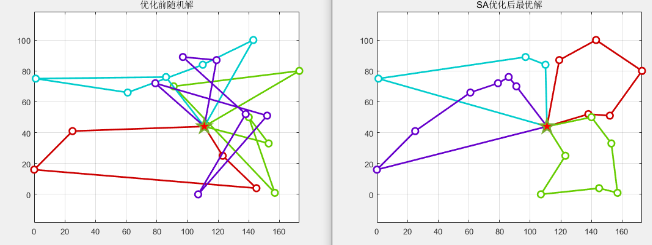
初始路径布局(左图):表示优化前的路径,各车辆服务的客户分布较分散,路径交叉较多,总成本较高。
-
优化后路径布局(右图):经过模拟退火算法优化后,路径更为合理,减少了不必要的路径交叉和距离,显著降低了总成本。
-
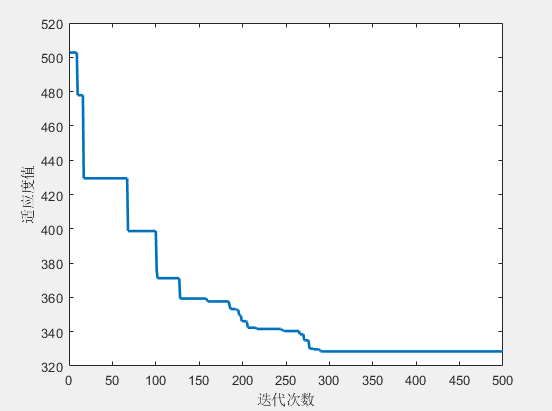
适应度收敛曲线(下图):显示了适应度值(总成本)在 500 次迭代中的变化过程。可以看到,适应度值在前期快速下降,逐渐收敛到稳定值,表明 SA 算法在 HFVRP 优化中具有较好的收敛性能。
部分代码
% 初始化参数
numVehicles = 5; % 车辆类型数量
numCustomers = 20; % 客户数量
initialTemp = 1000; % 初始温度
finalTemp = 1; % 最终温度
coolingRate = 0.95; % 降温速率
maxIter = 500; % 最大迭代次数% 随机生成客户位置和需求
customerLocations = rand(numCustomers, 2) * 100;
customerDemands = randi([1, 10], numCustomers, 1);% 初始解和适应度
currentSolution = initializeSolution(numVehicles, numCustomers);
currentCost = calculateCost(currentSolution, customerLocations, customerDemands);% 模拟退火过程
temp = initialTemp;
for iter = 1:maxIter% 生成新解并计算成本newSolution = perturbSolution(currentSolution);newCost = calculateCost(newSolution, customerLocations, customerDemands);% 判断是否接受新解if acceptSolution(currentCost, newCost, temp)currentSolution = newSolution;currentCost = newCost;end% 降温temp = temp * coolingRate;costHistory(iter) = currentCost; % 记录每次迭代的成本
end% 绘制适应度收敛曲线
figure;
plot(costHistory, 'LineWidth', 1.5);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度收敛曲线');% 绘制优化后路径
plotRoutes(currentSolution, customerLocations);
title('SA优化后路径布局');% 辅助函数
function solution = initializeSolution(numVehicles, numCustomers)% 初始化解决方案
endfunction cost = calculateCost(solution, locations, demands)% 计算路径总成本
endfunction newSolution = perturbSolution(solution)% 生成新解
endfunction accept = acceptSolution(currentCost, newCost, temp)% 判断是否接受新解if newCost < currentCostaccept = true;elseaccept = exp((currentCost - newCost) / temp) > rand();end
endfunction plotRoutes(solution, locations)% 绘制路径
end
参考文献
❝
Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by Simulated Annealing. Science, 220(4598), 671-680.
Laporte, G., & Nobert, Y. (1987). Exact Algorithms for the Vehicle Routing Problem. Annals of Discrete Mathematics, 31, 147-184.
Osman, I. H., & Laporte, G. (1996). Metaheuristics: A Bibliographic Survey. Annals of Operations Research, 63(5), 513-628.
(文章内容仅供参考,具体效果以图片为准)
