目录
前言:
正文:
题单:【237题】算法基础精选题单_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网 (nowcoder.com)
01背包:
NC16693 装箱问题:
NC16650 [NOIP2005]采药:
NC16666 [NOIP2006]开心的金明:
NC19158 失衡天平:
NC231128 Steadily Growing Steam:
完全背包:
NC21467 [NOIP2018]货币系统:
多重背包:
NC235950 多重背包:
分组背包:
NC16671 [NOIP2006]金明的预算方案:
二位费用背包:
NC14699 队伍配置:
map优化超大背包:
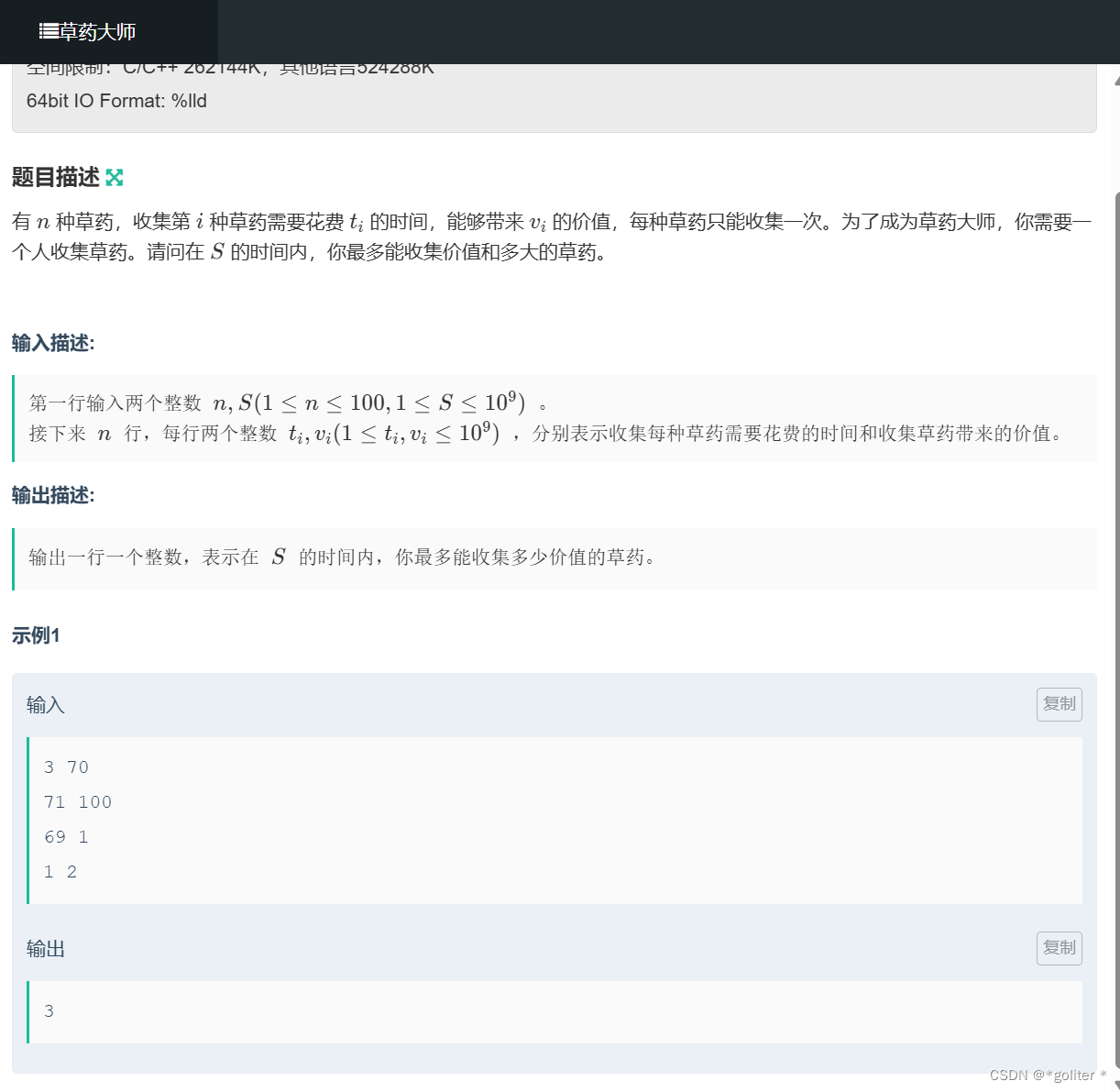
NC235951 草药大师:
后记:
前言:
背包问题是很经典的dp问题,从最简单的01背包问题衍生了很多其他更复杂的形式,在这我不详细介绍背包问题的动态转移公式的推导,感兴趣的可以在各个平台搜搜看,他们讲的肯定比我好。
正文:
题单:【237题】算法基础精选题单_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网 (nowcoder.com)
01背包:
NC16693 装箱问题:
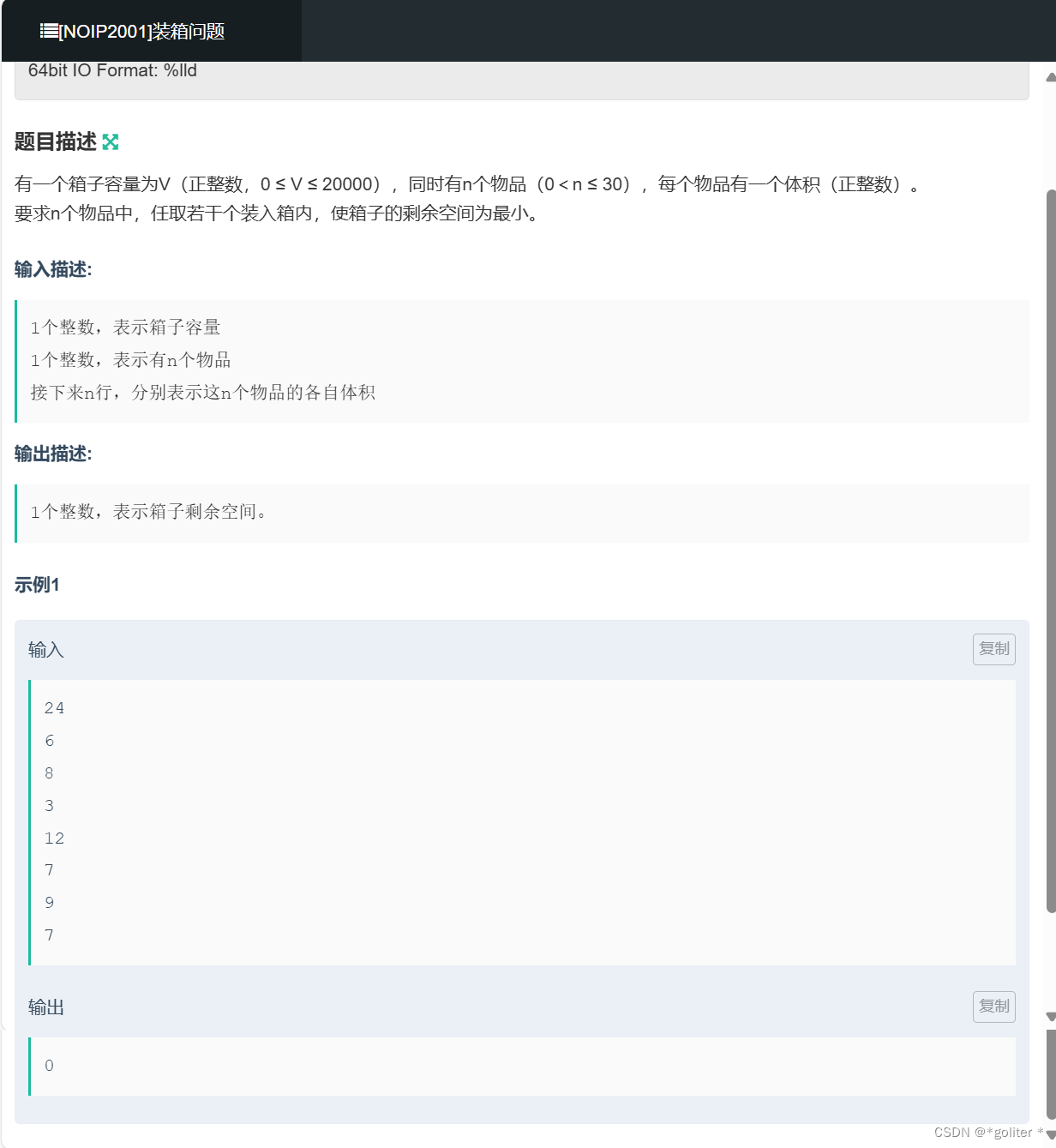
#include <bits/stdc++.h>
using namespace std;
int a[35];
int dp[200005];
int main(){int v,n;cin>>v>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){for(int j=v;j>=a[i];j--){dp[j]=max(dp[j-a[i]]+a[i],dp[j]);}}cout<<v-dp[v];return 0;
}NC16650 [NOIP2005]采药:
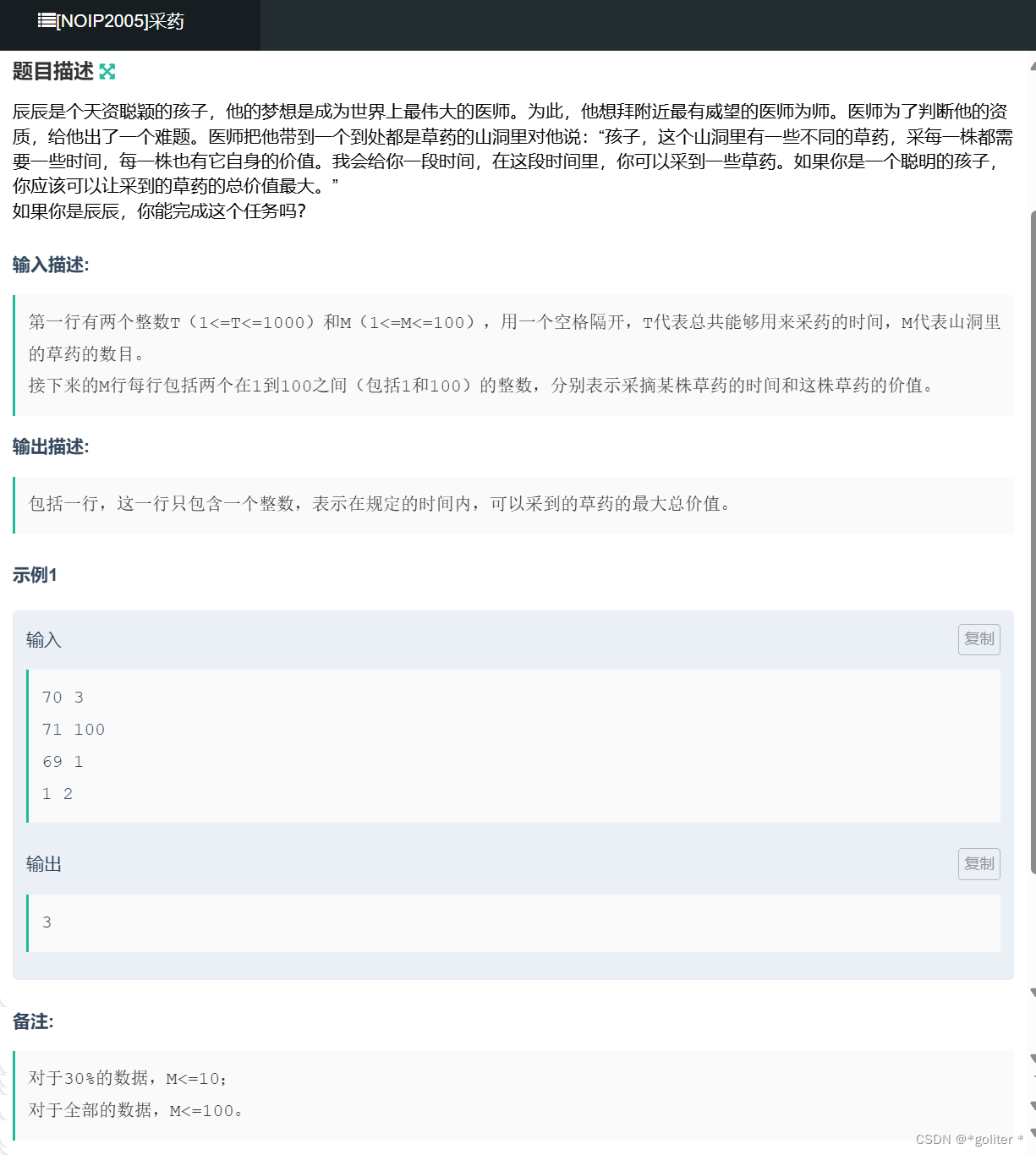
#include <bits/stdc++.h>
using namespace std;
int dp[100000];
int w[1005],v[1005];
int main(){int t,n;cin>>t>>n;for(int i=1;i<=n;i++){cin>>w[i]>>v[i];}for(int i=1;i<=n;i++){for(int j=t;j>=w[i];j--){dp[j]=max(dp[j],dp[j-w[i]]+v[i]);}}cout<<dp[t];return 0;
}NC16666 [NOIP2006]开心的金明:
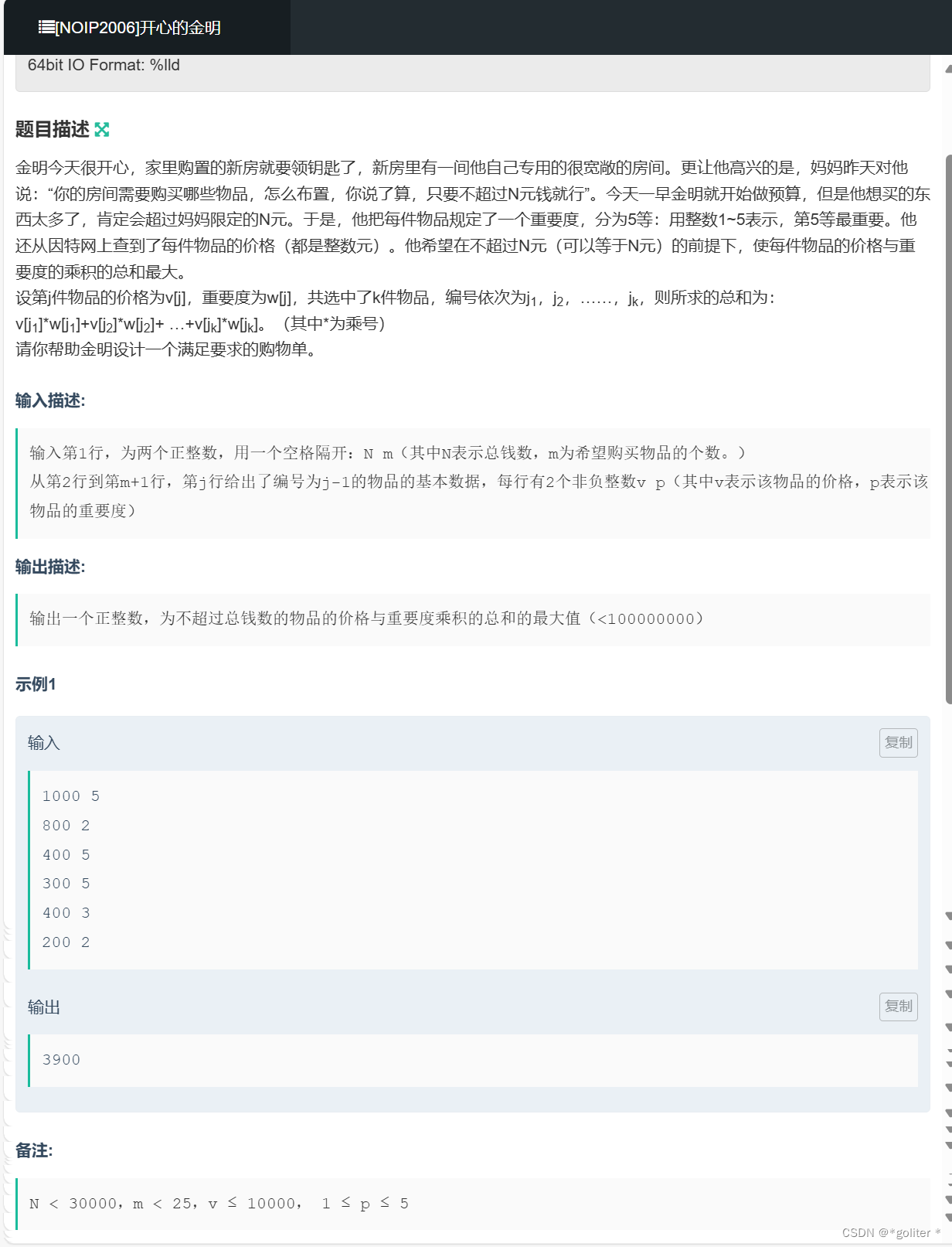
#include <bits/stdc++.h>
using namespace std;
int dp[30050];
int a[105],p[105];
int main(){int n,m;cin>>n>>m;for(int i=1;i<=m;i++)cin>>a[i]>>p[i];for(int i=1;i<=m;i++){for(int j=n;j>=a[i];j--){dp[j]=max(dp[j-a[i]]+a[i]*p[i],dp[j]);}}cout<<dp[n]<<endl;return 0;
}上面三道题基本上就是模板题,唯一要注意的就是第三题他物品的价值是价格乘重要度。
NC19158 失衡天平:
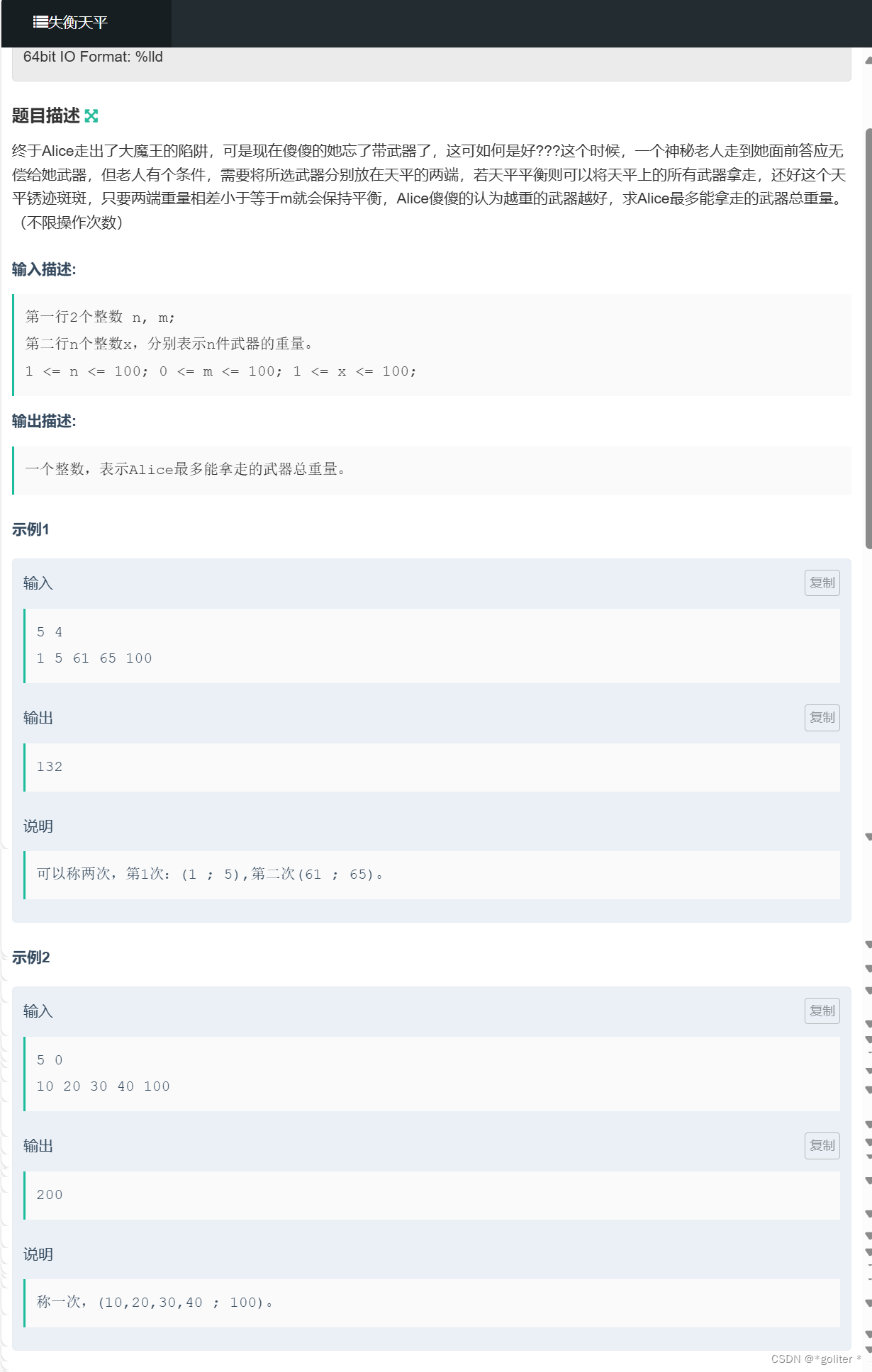
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int w[105];
int dp[105][N];
int main(){int n,m,ans=0;cin>>n>>m;for(int i=1;i<=n;i++){cin>>w[i];}memset(dp,-0x3f,sizeof(dp));dp[0][0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=300;j++){dp[i][j]=dp[i-1][j];dp[i][j]=max(dp[i][j],max(dp[i-1][abs(j-w[i])]+w[i],dp[i-1][j+w[i]]+w[i]));//cout<<i<<" "<<j<<" "<<dp[i][j]<<endl;}}for(int i=0;i<=m;i++){ans=max(dp[n][i],ans);//cout<<dp[n][i]<<endl;}cout<<ans<<endl;return 0;
}其实觉得这道题不像01背包,可能是取物品的思想比较类似吧,这里dp[i][j]的状态表示为取到第i个物品,天平差值为j时物品重量最大值,这个状态可以由以状态转移过来:
- 不拿第i个物品。
- 拿第i个物品并放在天平物品重量小的那一边
- 拿第i个物品并放在天平物品重量大的那一边
所以状态转移方程为(先事先把第一种情况转移)
这边要注意我们这种转移方式会引用到一些非法值(不可能转移到的值),所以我们要将处dp[0][0]以外的值都初始化为负无穷,以免将非法值转移过来。
最后枚举小于m的差值找出最大答案。
NC231128 Steadily Growing Steam:
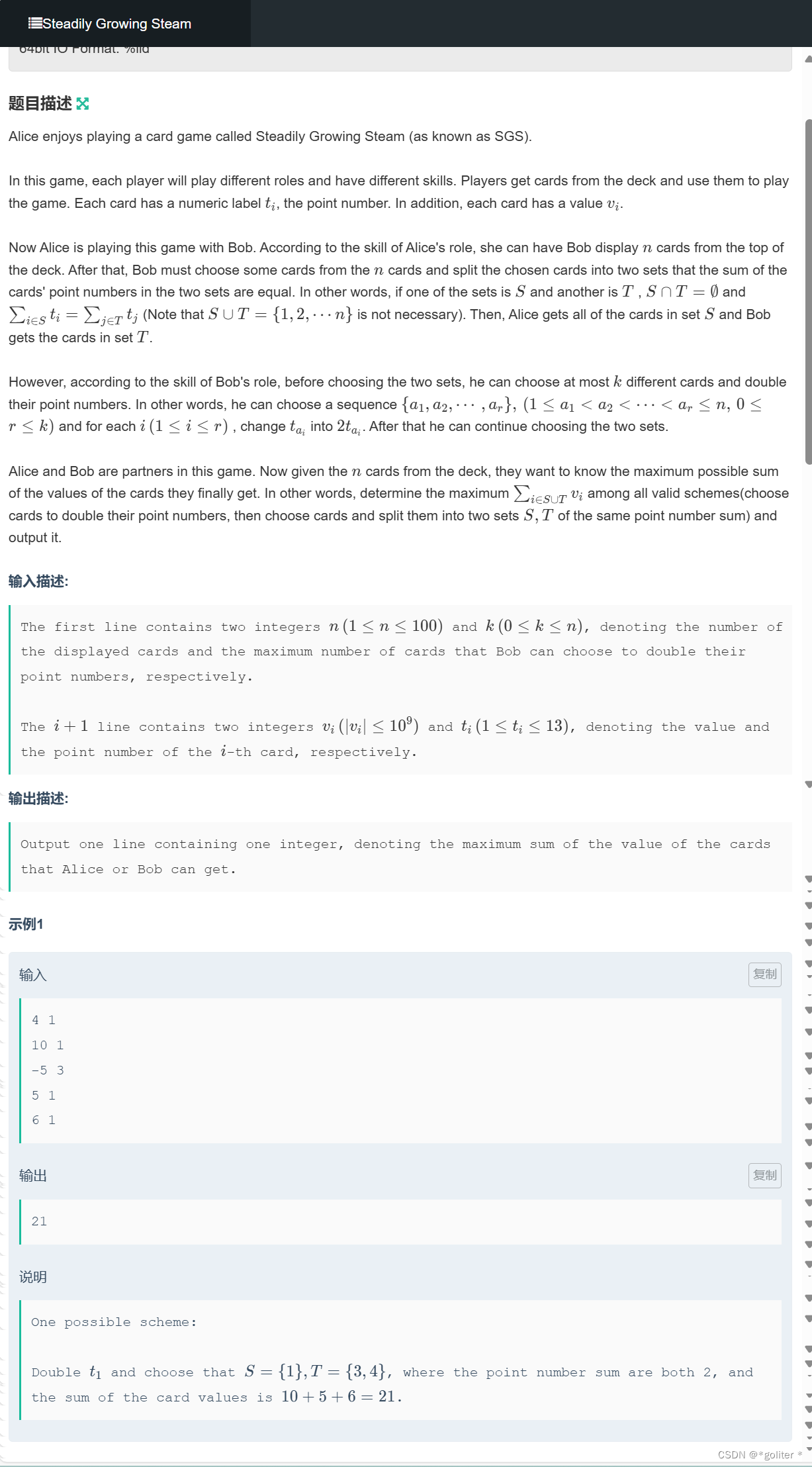
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[105],v[105],dp[105][105][1350];
int main(){int n,k;cin>>n>>k;for(int i=1;i<=n;i++){cin>>v[i]>>a[i];}memset(dp,-0x3f,sizeof(dp));dp[0][0][0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=k;j++){for(int k=0;k<=1350;k++){dp[i][j][k]=dp[i-1][j][k];dp[i][j][k]=max(dp[i][j][k],max(dp[i-1][j][abs(k-a[i])]+v[i],dp[i-1][j][abs(k+a[i])]+v[i]));if(j!=0)dp[i][j][k]=max(dp[i][j][k],max(dp[i-1][j-1][abs(k-a[i]*2)]+v[i],dp[i-1][j-1][abs(k+a[i]*2)]+v[i]));//cout<<i<<" "<<j<<" "<<k<<" "<<dp[i][j][k]<<endl;}}}ll ans=0;for(int i=0;i<=k;i++){ans=max(ans,dp[n][i][0]);}cout<<ans<<endl;return 0;
}上题的hard版,加上了k次翻倍的能力,并且这次要求两边完全相等,所以我们的转移方程就比上一题要有点不同了:
- 不选当前的卡片:dp[i][j][k] = dp[i-1][i][j];
- 选当前的卡片但将其放到点数大的那一个里面(不使用技能):dp[i][j][k] = max(dp[i][j][k], dp[i-1][j][k+a[i].point]+a[i].v)
- 选当前的卡片但将其放到点数小的那一个里面(不使用技能):dp[i][j][k] = max(dp[i][j][k], dp[i-1][j][abs(k-a[i].point)]+a[i].v)
- 选当前的卡片但将其放到点数大的那一个里面(使用技能):dp[i][j][k] = max(dp[i][j][k], dp[i-1][j-1][k+a[i].point]+a[i].v)
- 选当前的卡片但将其放到点数小的那一个里面(使用技能):dp[i][j][k] = max(dp[i][j][k], dp[i-1][j-1][abs(k-a[i].point)]+a[i].v)
最后枚举翻倍次数到k,找到最大的卡牌值。
完全背包:
NC21467 [NOIP2018]货币系统:
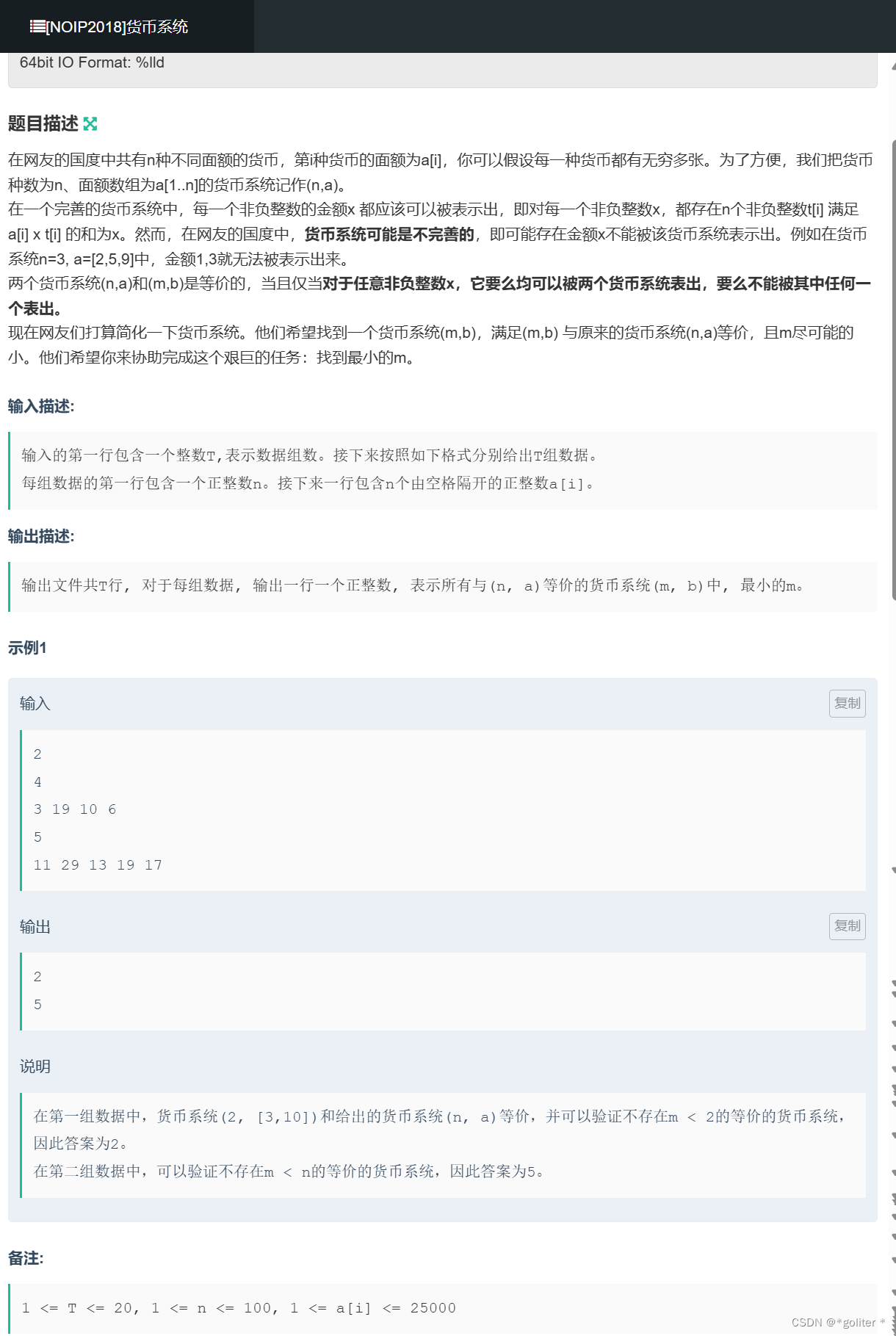
#include<bits/stdc++.h>
using namespace std;
int a[105],dp[25005];
int main(){int t;cin>>t;while(t--){int n;cin>>n;memset(dp,0,sizeof(dp));for(int i=1;i<=n;i++){cin>>a[i];}sort(a+1,a+n+1);dp[0]=1;int ans=n;for(int i=1;i<=n;i++){if(dp[a[i]]==1){ans--;continue;}else{for(int j=a[i];j<=a[n];j++){dp[j]=dp[j]||dp[j-a[i]];}}}cout<<ans<<endl;}return 0;
}理解题意我们很容易知道一种货币如果可以由其他货币表示那么他就是没有存在必要的,所以我们先将货币按大小排序,从小到大进行多重背包,如果这个货币能被之前的货币表示就标记并让答案-1(答案初值设为n)。
多重背包:
NC235950 多重背包:
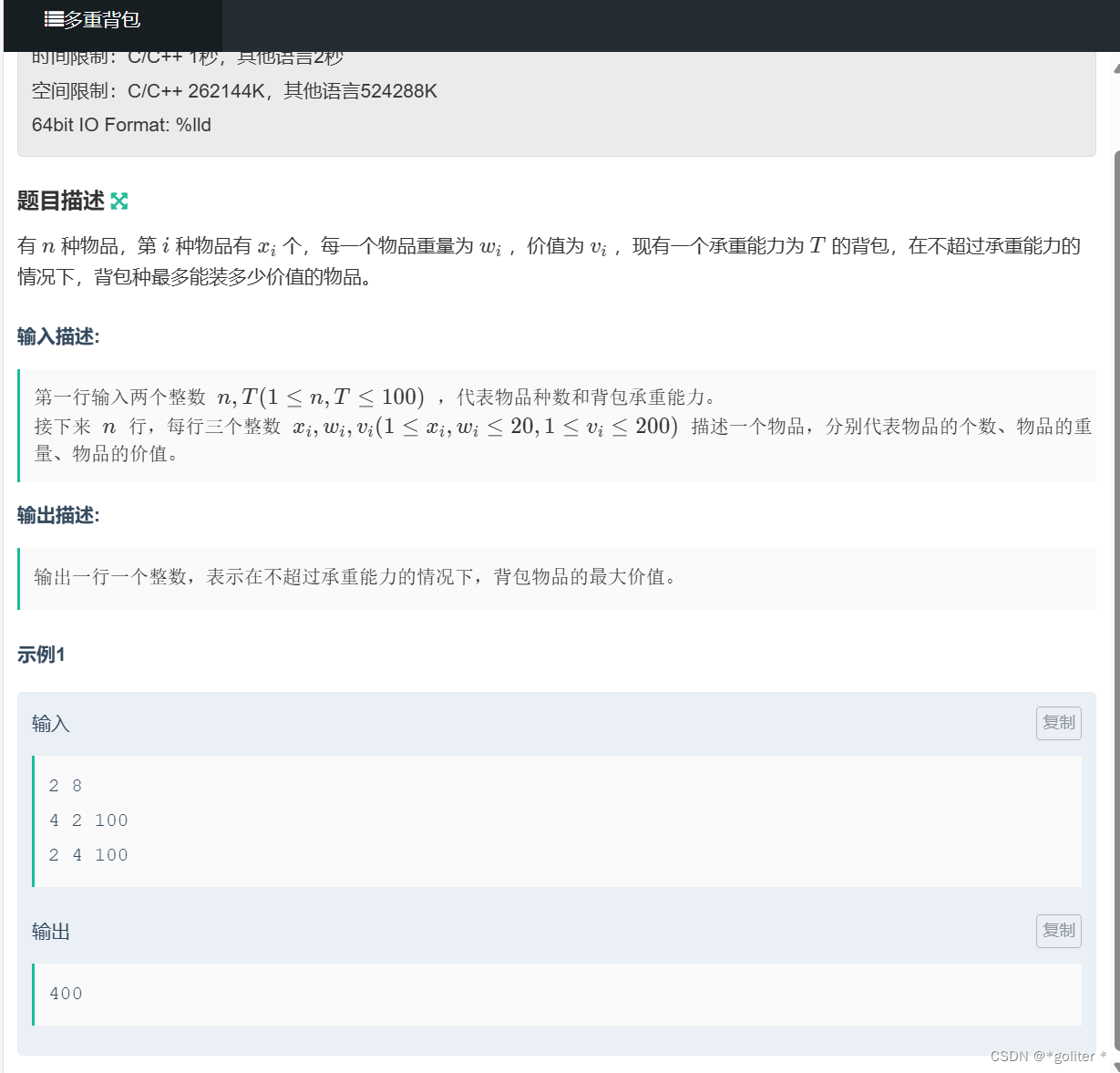
#include <bits/stdc++.h>
using namespace std;
const int N = 11010, M = 2010;
int w[N], v[N];
int dp[M];
int main(){ios::sync_with_stdio(false);int n,m;cin>>n>>m;int cnt=0;while(n--){int b,a,s;//a是重量,b是价值,s是数量cin>>s>>a>>b;for(int k=1;k<=s;k*=2){cnt++;w[cnt]=a*k,v[cnt]=b*k;s-=k;}if(s>0){cnt++;w[cnt]=a*s,v[cnt]=b*s;}}n=cnt;for(int i=1;i<=n;i++)for(int j=m;j>=w[i];j--)dp[j]=max(dp[j],dp[j-w[i]]+v[i]);cout<<dp[m]<<"\n";return 0;
}多重背包模板。
分组背包:
NC16671 [NOIP2006]金明的预算方案:
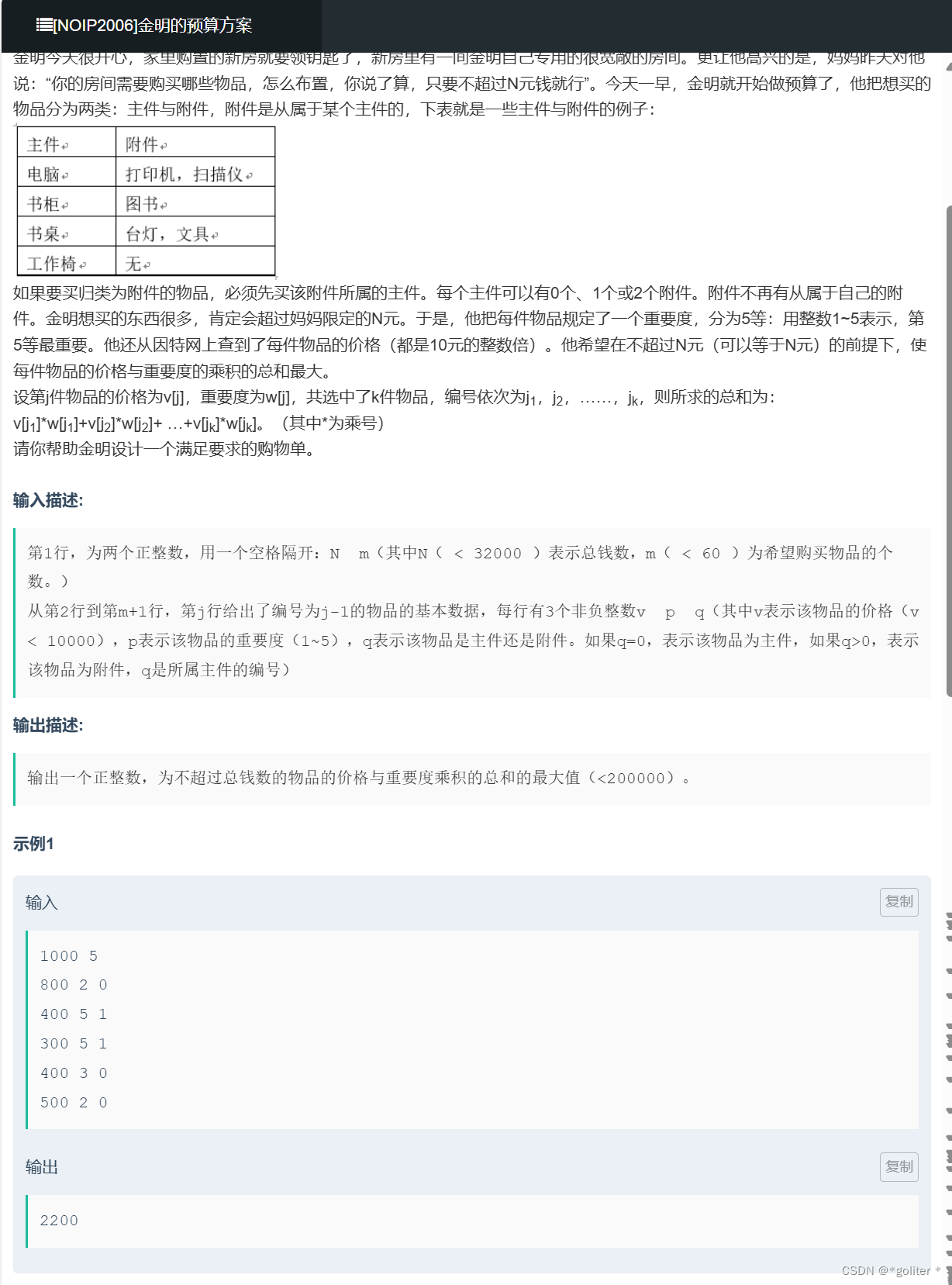
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef struct stu{int v;int p;
}node;
node a[65];
vector<node> aa[65];
int dp[32005];
int main(){int n,m;cin>>n>>m;for(int i=1;i<=m;i++){int v,p,q;cin>>v>>p>>q;p=p*v;if(q==0){a[i].v=v;a[i].p=p;}else{aa[q].push_back({v,p});}}for(int i=1;i<=m;i++){if(!a[i].v)continue;for(int j=n;j>=0;j--){for(int l=0;l<=3;l++){int v=a[i].v;int p=a[i].p;for(int k=0;k<aa[i].size();k++){if((l>>k)&1){v+=aa[i][k].v;p+=aa[i][k].p;}}if(j>=v)dp[j]=max(dp[j],dp[j-v]+p);}//cout<<dp[j]<<endl;}}cout<<dp[n]<<endl;return 0;
}因为要买附件必须有主件,并且一个主件最多带有两个附件,那么状态最多就由五个状态表示出来:
- 不选,然后去考虑下一个
- 选且只选这个主件
- 选这个主件,并且选附件1
- 选这个主件,并且选附件2
- 选这个主件,并且选附件1和附件2。
所以最后我们用vector处理附件后就直接开始枚举主件,每个主件可以派生最多五种选择,这不就是多重背包模型吗,最后可以通过二进制操作来枚举这五种情况,然后通过转移方程来求最大值。
二位费用背包:
NC14699 队伍配置:

#include<bits/stdc++.h>
using namespace std;
long long dp[200][10][10];
int main(){long long n,m,d,ans=0;cin>>n>>m>>d;memset(dp,-0x3f3f3f,sizeof(dp));dp[0][0][0]=0;for(int i=1;i<=n;i++){int a,b;cin>>a>>b;for(int j=d;j>=b;j--){for(int k=1;k<=5;k++){dp[j][k][0]=max(dp[j][k][0],dp[j-b][k-1][0]+a);ans=max(ans,dp[j][k][0]);}}}for(int i=1;i<=m;i++){int a,b;cin>>a>>b;for(int j=d;j>=b;j--){for(int k=1;k<=5;k++){for(int l=1;l<=k;l++){dp[j][k][l]=max(dp[j][k][l],dp[j-b][k][l-1]+a);ans=max(ans,dp[j][k][l]);}}}}cout<<ans<<endl;return 0;
}先枚举从者不带礼装的情况,之后再来枚举礼装的情况(礼装的内部分配对于最后的结果是不影响的)。状态dp[i][j][k]表示费用为i,从者数量为j,礼装数量为k时atk的最大值。两个状态转移易知为
最后从每一个状态中挑最大值即为答案。
map优化超大背包:
NC235951 草药大师:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
map<ll,ll> dp;
int main(){int n,s;cin>>n>>s;dp[0]=0;for(int i=1;i<=n;i++){int t,v;cin>>t>>v;for(map<ll,ll>::reverse_iterator it=dp.rbegin();it!=dp.rend();it++){if((it->first)+t<=s){dp[it->first+t]=max(dp[it->first+t],dp[it->first]+v);//cout<<dp[it->first+t]<<endl;//cout<<i<<" "<<it->first+t<<" "<<dp[it->first+t]<<endl;}//cout<<i<<" "<<it->first+t<<" "<<dp[it->first+t]<<endl;}}ll ans=0;for(map<ll,ll>::iterator it=dp.begin();it!=dp.end();it++){ans=max(ans,it->second);}cout<<ans<<endl;return 0;
}这种背包没见过,所以我直接奔着题解去了,其实就是在普通的01背包中优化第二层循环,原先我们时一步一步加一枚举过去的,用map的话就可以只枚举已经出现过的部分,大大优化了空间和时间,最终map中的数据就为所有可能会出现的数据。
值得一提的是在我本地的编译器上运行这串代码的结果竟然和牛客上不一样?发给我同学在他们电脑上跑的结果与我的还不一样?不知道是不是我的编译器版本太老了。
后记:
这下简单的dp问题就都解决了,剩下的树形dp和状压dp估计够我写的了(。
