【初阶数据结构题目】23. 向上调整算法

向上调整算法

堆的插入

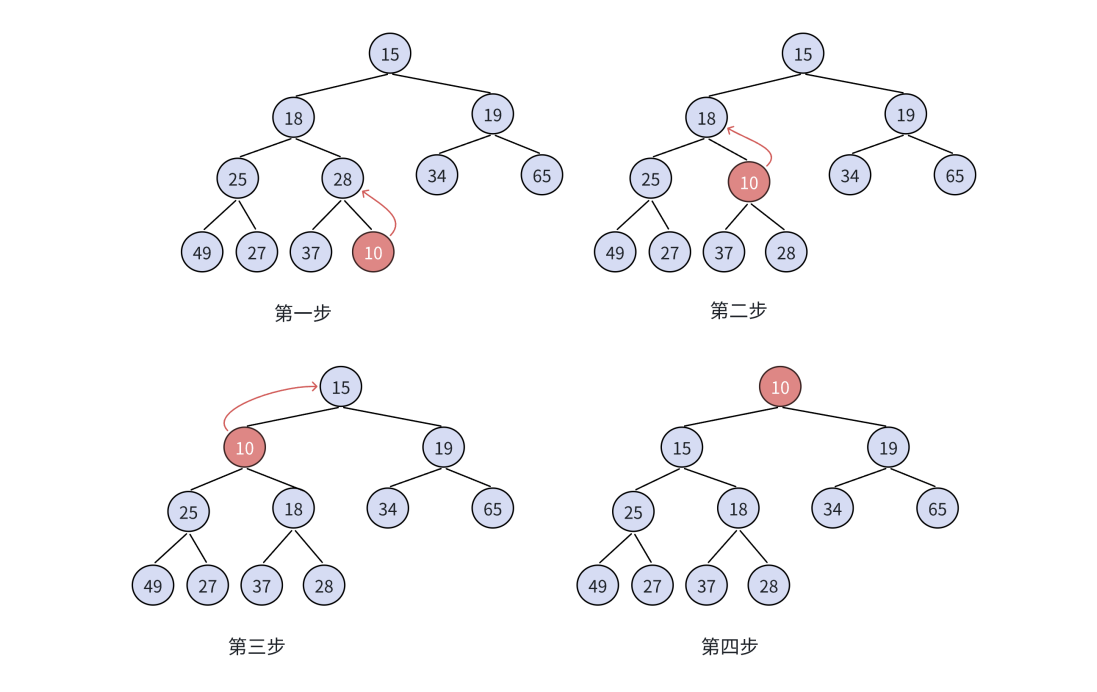
将新数据插入到数组的尾上，再进行向上调整算法，直到满足堆。

向上调整算法

• 先将元素插入到堆的末尾,即最后一个孩子之后

• 插入之后如果堆的性质遭到破坏，将新插入结点顺着其双双亲往上调整到合适位置即可

void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while(child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}
void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size-1);
}

计算向上调整算法建堆时间复杂度：

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个结点不影响最终结果)

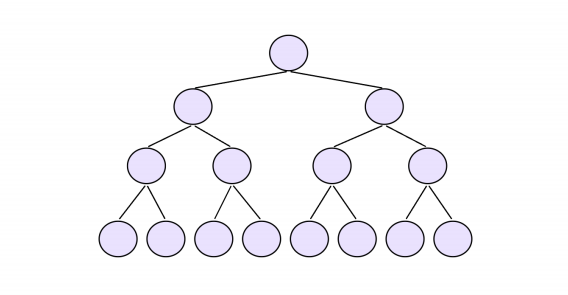
如果是根节点，不需要向上调整。

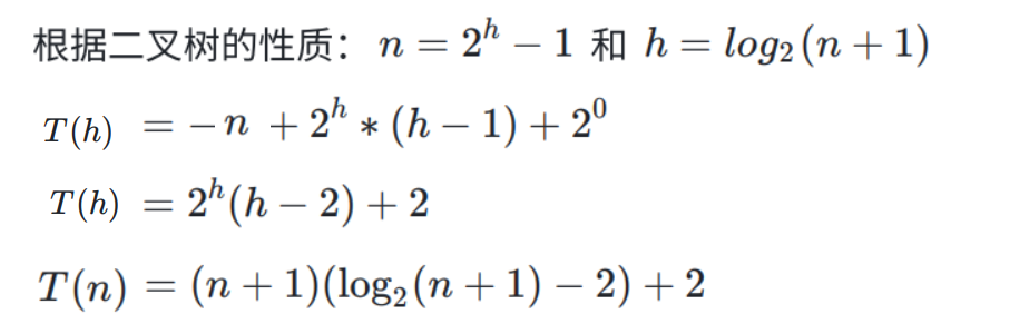
1. T(n)：这个表达式代表的是在堆的向上调整算法中，对于一个具有n个节点的堆，完成调整所需的移动步数。

   通过分层说明和移动步数计算解释，给出了一个关于h（堆的高度）的函数表达式，并最终通过一系列变换得到了T(h)的表达式。

2. F(h)：这个表达式代表的是在堆的向上调整算法中，对于高度为h的堆，完成调整所需的移动步数的另一种表达形式。

   最终目的是为了推导出F(n)。

3. F(n)：这个表达式代表的是对于具有n个节点的堆，完成向上调整所需的移动步数的最终表达式。通过将T(h)的表达式转换为关于n的表达式，得到了F(n)的表达式。

   这个表达式是基于二叉堆的性质，即堆的节点数n与堆的高度h之间的关系==（n = 2^h - 1），以及高度h与节点数n之间的关系（h = log₂(n + 1)）==。

由此可得：

向上调整算法建堆时间复杂度为：O(n ∗ log₂n)