1.“八皇后问题”描述:
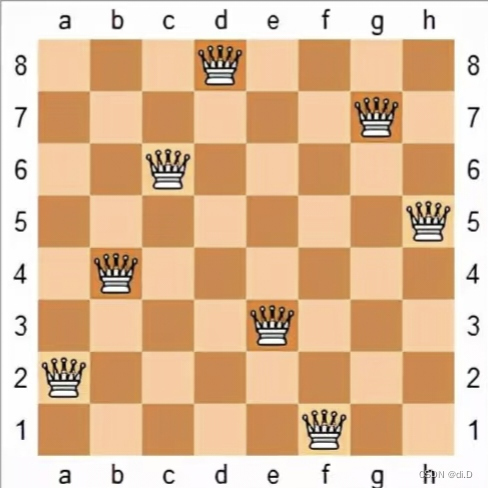
八皇后问题是一个经典的用回溯法来求解的问题。它要求在一个8*8的棋盘上放上8个皇后,使得每一个皇后既攻击不到另外七个皇后,也不被另外七个皇后所攻击。故八皇后问题即:求八皇后的某种布局,使得任意两个皇后不在同一行、同一列或同一斜线上。
2.算法分析:
在程序设计中有一种方法叫做“回溯法”。它不是按照某种公式或确定的法则求问题的解,而是通过试探并纠正错误的策略,找到问题的解。它采用了一种“走不通就掉头”思想作为其控制结构,相当于采用了先根遍历的方法来构造解答树,可用于找一组解、所有解或最优解。回溯法被用于人工智能领域,而且经常用它来解决八皇后问题。
①回溯法的基本思想:
首先确定问题的解空间结构,然后按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先的策略进行搜索。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于求解一些解空间较大的问题。
②回溯法的一般步骤:
1)针对所给问题,定义问题的解空间。
2)确定易于搜索的解空间结构。
3)以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。在搜索过程中,通常采用两种策略避免无效搜索:一是用约束函数剪去得不到可行解的子树;二是用限界函数剪去得不到最优解的子树。这两类函数统称为剪枝函数。
3.代码实现:
#include <iostream>
using namespace std;
// 位运算解决八皇后问题
void solveNQueens(int n) {long upperlim = (1 << n) - 1; // 初始化,upperlim 表示 n 个皇后的所有列都已放置好long Ans = 0; // 记录解的个数// 递归函数,寻找可以放置皇后的位置void test(long row, long ld, long rd) {if (row != upperlim) {// pos 表示当前行可以放置皇后的位置long pos = upperlim & (~(row | ld | rd));while (pos) {// 取出最右边的可以放皇后的位置long p = pos & (-pos);pos -= p; // 移除该位置并递归调用 test 过程// 更新限制条件long new_ld = (ld | p) << 1;long new_rd = (rd | p) >> 1;test(row | p, new_ld, new_rd);}} else {++Ans; // 找到一个解}}// 调用参数test(0, 0, 0);cout << "共有 " << Ans << " 种排列" << endl;
}
int main() {int n = 8; // 八皇后问题solveNQueens(n);return 0;
}