257. 二叉树的所有路径
题目
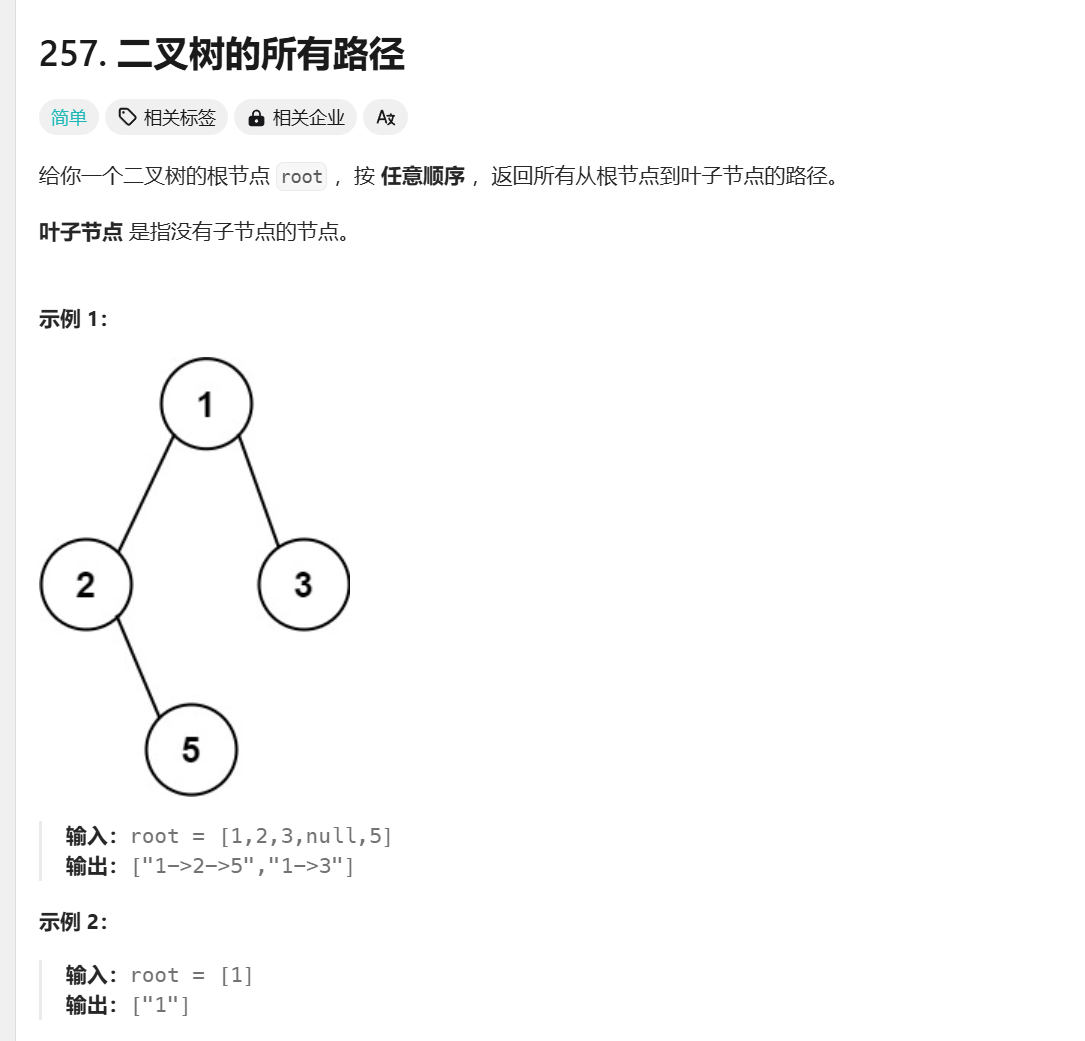
解决
做法一:深度优先搜索 + 回溯
深度优先搜索(Depth-First Search, DFS)是一种用于遍历或搜索树或图的算法。这种搜索方式会尽可能深地探索每个分支,直到无法继续深入为止,然后回溯到上一个节点,继续探索其他未访问的分支。
回溯我的个人理解是回退到之前的状态
大致想法:就是使用递归,在递归过程中使用 StringBuilder 存储路径上的节点和 箭头指向字符,直到 TreeNode 节点中左子节点 和 右子节点 都为空,将 StringBuilder 中存的依赖路径 加入到 list 中,每当退出递归,就回溯(将加入的 (节点值 + "->") 删除掉)
/*** 执行用时分布 5 ms 击败 30.20% 复杂度分析 消耗内存分布 41.53 MB 击败 70.56%*/
public List<String> binaryTreePaths(TreeNode root) {List<String> list = new ArrayList<>();StringBuilder path = new StringBuilder();path.append(root.val);// 递归获取 根节点到 叶子节点的路径getPath(root, path, list);return list;
}/*** 递归获取 根节点到 叶子节点的路径*/
public void getPath(TreeNode root, StringBuilder path, List<String> list) {// 递归边界就是 叶子节点,碰到叶子节点则递归结束,并将叶子节点的路径加入到结果集if (root.left == null && root.right == null){list.add(path.toString());return;}if (root.left != null){String pathStr = "->" + root.left.val;// 将 左子树节点的值加入到 树路径中path.append(pathStr);// 递归左子树getPath(root.left, path, list);// 回溯,将当前节点的左节点剔除出 字符串path.delete(path.length() - pathStr.length(), path.length());}if (root.right != null){String pathStr = "->" + root.right.val;path.append(pathStr);getPath(root.right, path, list);path.delete(path.length() - pathStr.length(), path.length());}
}优化
做法上基本是这样,但是时间上呢还是太慢了,根据以往经验发现可以将字符串替换成 栈 这个数据结构,弹出一个节点,可比 StringBuilder 删除来得快,StringBuilder.delete 底层是将整个字符数组拷贝的,相比于 栈 他是先进后出的,从栈顶弹出元素相对较快。
Deque 参考链接:双端队列 【Deque】-CSDN博客
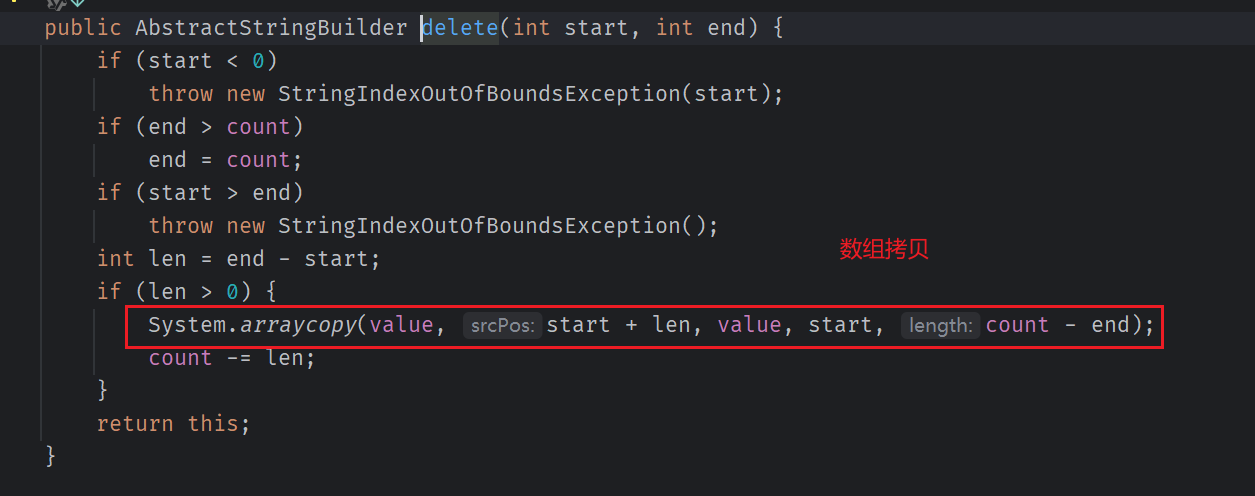
时间复杂度:O(nlogn);空间复杂度:O(nlogn)
因为遍历到叶子节点之后,还需要遍历 栈,最环的情况是 叶子节点的数量为 n/2,每个路径字符串的长度为 log(n)(因为完全二叉树的高度为 log(n))
/*** 执行用时分布 3 ms 击败 33.70% 复杂度分析 消耗内存分布 41.55 MB 击败 64.43%*/
public List<String> binaryTreePaths(TreeNode root) {List<String> list = new ArrayList<>();// 双端队列Deque<Integer> path = new LinkedList<>();// 递归获取 根节点到 叶子节点的路径getPath(root, path, list);return list;
}/*** 递归获取 根节点到 叶子节点的路径*/
public void getPath(TreeNode root, Deque<Integer> path, List<String> list) {if (root == null){return;}if (root.left == null && root.right == null){StringBuilder builder = new StringBuilder();// 遍历,组合成路径字符串path.forEach(val -> {builder.append(val).append("->");});// 加入当前叶子节点的 值builder.append(root.val);list.add(builder.toString());return;}// 因为回溯需要将,当前节点弹出并且需要按顺序循环遍历出来,所以选用 尾部插入,尾部弹出// 将当前节点加入path.add(root.val);// 递归左子树getPath(root.left, path, list);// 递归右子树getPath(root.right, path, list);// 回溯path.removeLast();
}做法二:深度优先搜索
参考官解:. - 力扣(LeetCode)
这里相对于上面快,是因为这里不需要回溯,使用的是局部变量
/*** 参考官解:https://leetcode.cn/problems/binary-tree-paths/solutions/400326/er-cha-shu-de-suo-you-lu-jing-by-leetcode-solution/* 深度优先遍历解法* 执行用时分布 1 ms 击败 99.56% 复杂度分析 消耗内存分布 41.57 MB 击败 58.89%*/
public List<String> binaryTreePaths(TreeNode root) {List<String> list = new ArrayList<>();// 递归获取 根节点到 叶子节点的路径getPath(root, "", list);return list;
}/*** 递归获取 根节点到 叶子节点的路径*/
public void getPath(TreeNode root, String path, List<String> list) {if (root == null){return;}StringBuilder builder = new StringBuilder(path);builder.append(root.val);if (root.left == null && root.right == null){list.add(builder.toString());return;}builder.append("->");// 递归左子树getPath(root.left, builder.toString(), list);// 递归右子树getPath(root.right, builder.toString(), list);
}做法三:广度优先遍历
广度优先遍历
广度优先遍历(Breadth-First Search, BFS)是一种用于图或树的遍历算法。这种搜索方式从根节点(或任意一个起始节点)开始,逐层访问每个节点的邻居节点,直到所有可达节点都被访问到。BFS 的特点是先访问离起点最近的节点,然后再逐步向外扩展。
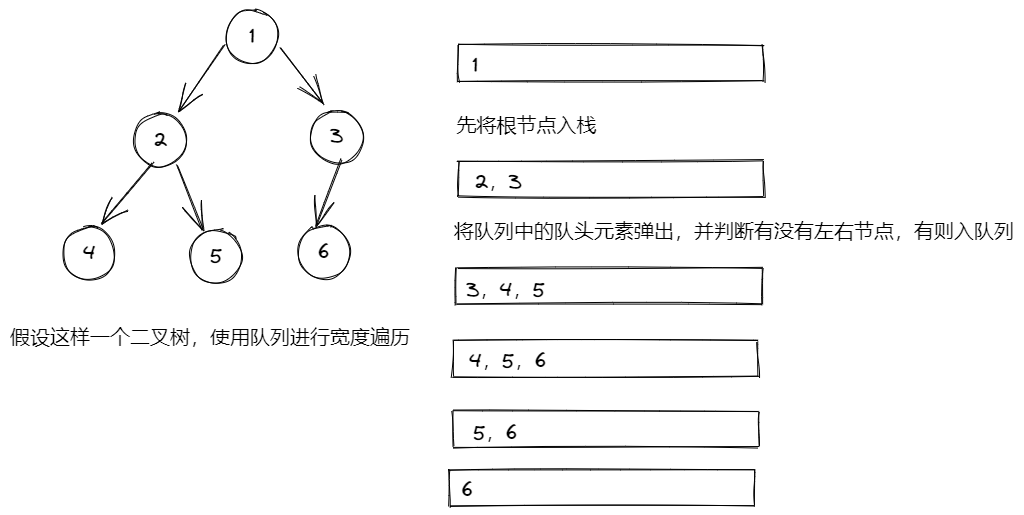
/*** 宽度遍历/广度优先遍历* @param head*/
private static void levelOrder(Node head){if (head == null) {return;}Queue<Node> queue = new LinkedList<>();queue.offer(head);while (!queue.isEmpty()){head = queue.poll();System.out.print(head.value + " ");if (head.left != null){queue.offer(head.left);}if (head.right != null){queue.offer(head.right);}}
}代码
/*** 广度优先搜索* 执行用时分布 2 ms 击败 47.70% 复杂度分析 消耗内存分布 41.48 MB 击败 79.08%*/
public List<String> binaryTreePaths(TreeNode root) {// 存储结果集List<String> result = new ArrayList<>();// 用于遍历存储节点Queue<TreeNode> nodeQueue = new LinkedList<>();// 用于存储 nodeQueue 的依赖路径Queue<String> pathQueue = new LinkedList<>();// 先将 根节点 加入队列用于遍历nodeQueue.add(root);// 将路径同步加入pathQueue.add(Integer.toString(root.val));// 遍历知道所有节点为空while (!nodeQueue.isEmpty()){// 弹出节点和路径TreeNode node = nodeQueue.poll();String path = pathQueue.poll();// 叶子节点if (node.left == null && node.right == null) {result.add(path);continue;}// 如果左子节点不为空就将节点加入到队列中,并将依赖路径拼接好加入队列if (node.left != null){nodeQueue.add(node.left);pathQueue.add(new StringBuilder(path).append("->").append(node.left.val).toString());}if (node.right != null){nodeQueue.add(node.right);pathQueue.add(new StringBuilder(path).append("->").append(node.right.val).toString());}}return result;
}