目录
前言
一.快排介绍与思想
二.hoare版本
2.0算法思想
2.1单趟过程
2.2多趟过程的思想
三.快排的优化
3.1随机数法选key
3.2三数取中选key
3.3小区间改造
四.挖坑法
四.前后指针法
六.利用栈将递归改非递归
后语
前言
本篇博客难度较高,建议在学习过程中先阅读一遍思路、浏览一遍动图,之后研究代码,之后仔细体会思路、体会动图。之后再自己进行实现。
一.快排介绍与思想
快速排序相当于一个对冒泡排序的优化,其大体思路是先在文中选取一个数作为基准值,将数组分为两个区间,一个区间比这个数大,另一个区间比这个数小。不断进行这个操作,直到我们的区间内只有一个数为止。
因此,快速排序的步骤如下:
- 1.先从数列中取出一个数作为基准数。
- 2.将数组分区间,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
- 3.再对左右区间重复这个动作,直到各区间只有一个数。
快速排序有多个版本,分别有hoare大佬创建的版本:hoare版本;便以理解的挖坑法;以及效率很高的前后指针法。我们依次讲解这些版本
二.hoare版本
2.0算法思想
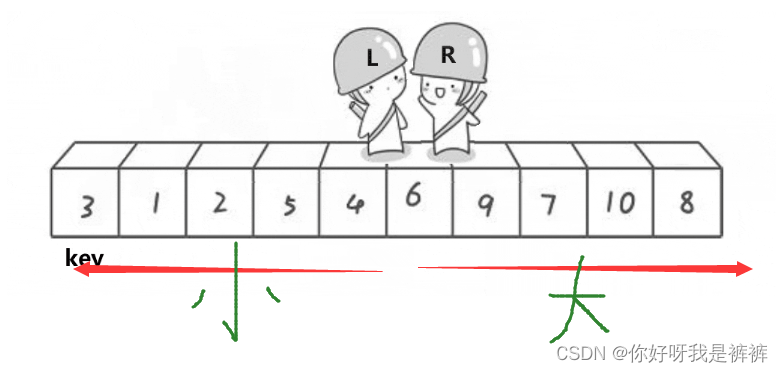
首先,我们定义两个指针,分别指向两个数组的最左侧和最右侧。
之后,让R(小人头盔)去找比key小的数,L去找比key大的数,都找到了之后交换L和R的数。
然后再让他们继续走,继续找,继续交换,直到他们相遇为止。
此时将相遇处的值与key交换,此时相遇处右侧都是比key大的数,左侧都是比key小的数。
整个过程如下:
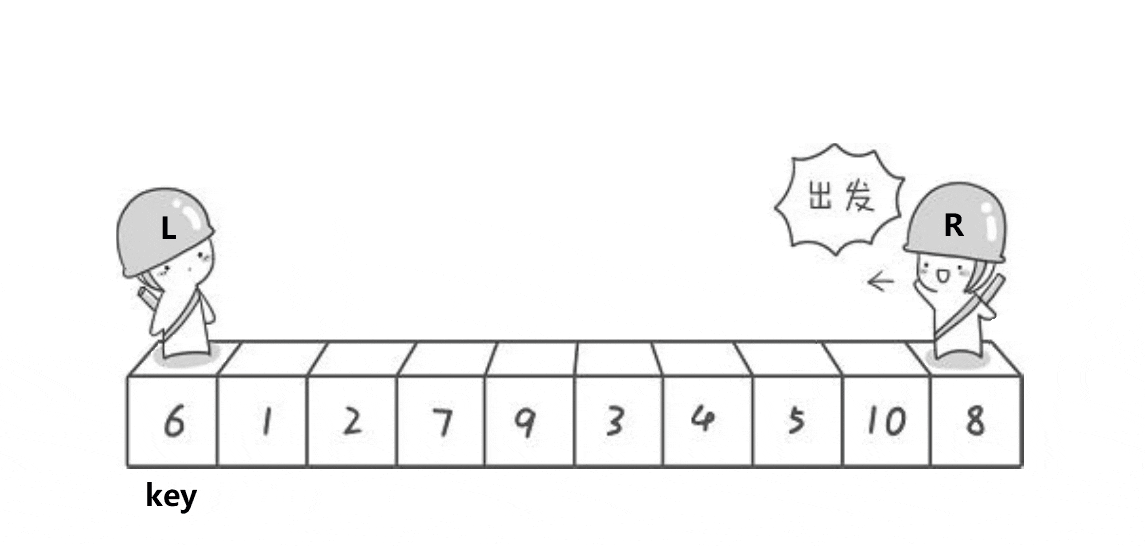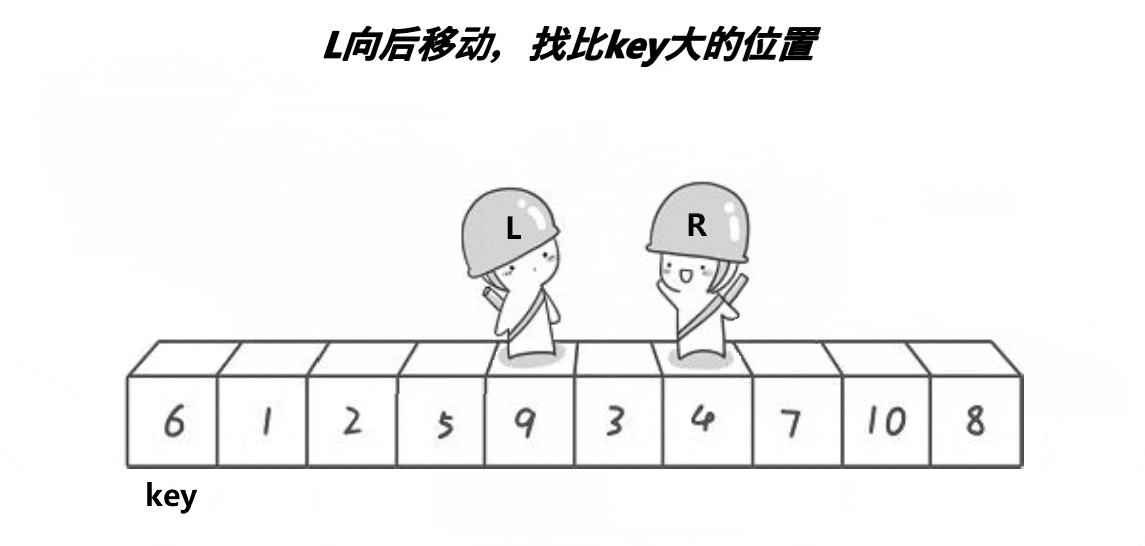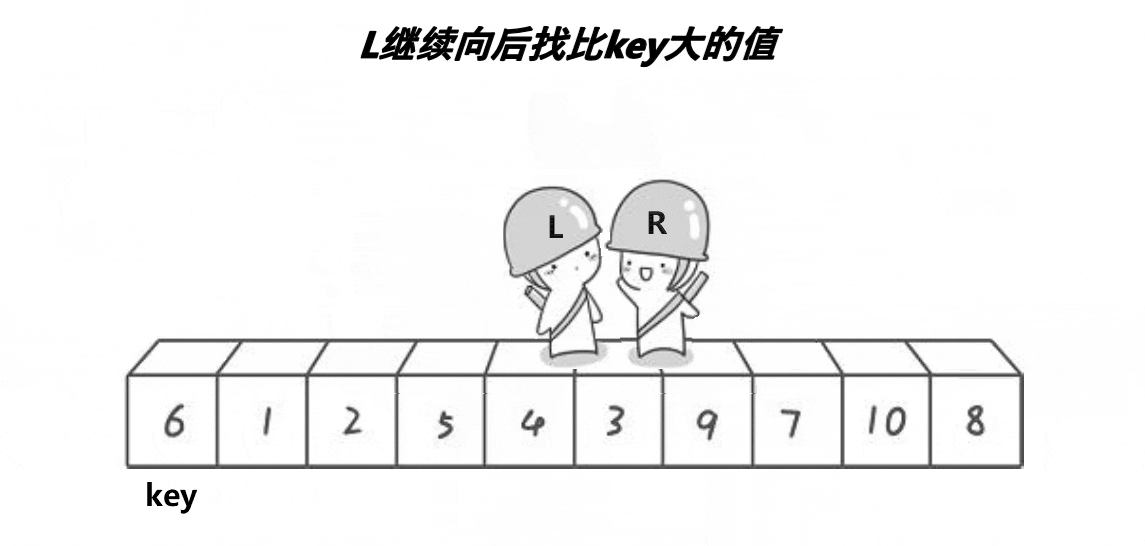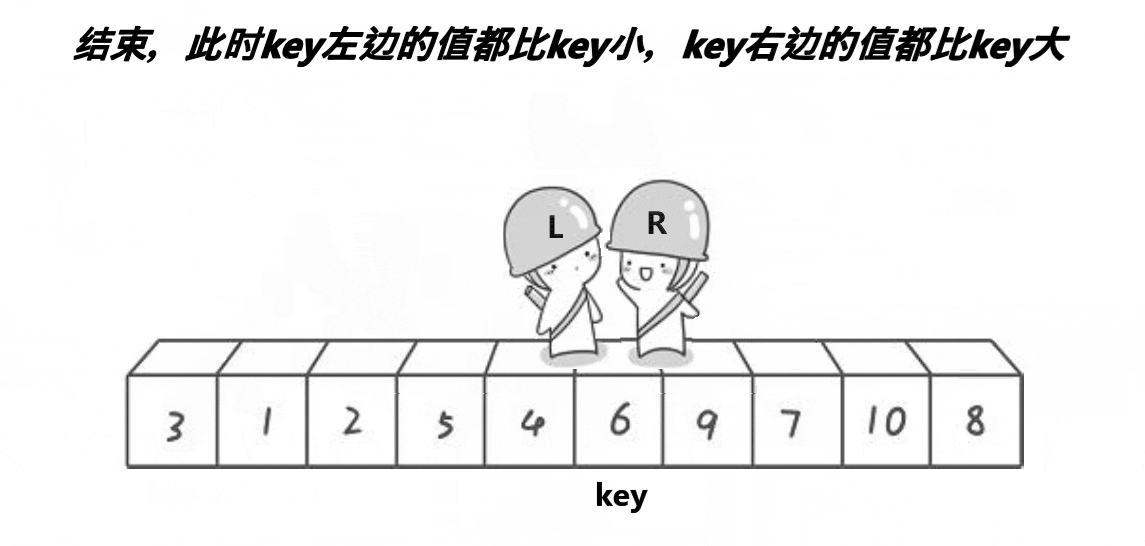
之后我们选定新的基准值,并不断进行上述动作,即可让大的数在右侧,小的数在左侧。
2.1单趟过程
- 我们首先选定数组下标为0处的值为基准值
- 之后便是让right先走,找到较小的数
- left再走,找到较大的数字
- 交换left和right的数
- right再走,找小
- left再走,找大
- 相遇时,将相遇处的值和keyi的值交换,并将相遇处的坐标设置为新的新keyi
现在我们将这一个过程实现为代码:
//keyi-->begin处的数据下标int keyi = begin;int left = begin;int right = end;while (left < right){//right先走,找小 找小,所以大于的时候要right--while(left < right && a[right] >= a[keyi]){--right;}//left再走,找大while(left < right&& a[left] <= a[keyi]){--left;}swap(&a[left], &a[right]);}keyi = left;下面我们来剖析一下这段代码
- 首先,我们的右指针是要找到小了才会停下来的,因此我们需要用到循环才能保证它找到小的时候停下来
- 我们要找到小的时候停下来,就代表找到小是退出循环的条件,因此我们的条件是a[right] >= a[keyi]
- 另外,我们一定要在while循环内部判断left<right,否则很容易发生数组越界。
如下图,如果我们不判断等于的话,则会出现死循环;

若我们不判断left<right的话,则很容易走出循环,譬如下图的情况,right一直找不到小,就走出循环了。
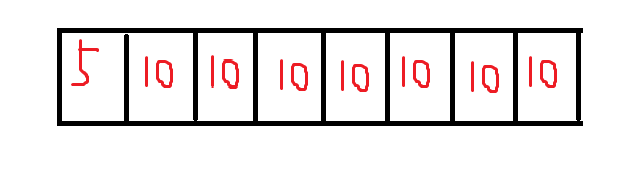
然后我们再来分析另外一个问题
如果相遇处的值大于keyi怎么办?它大于keyi的话,交换后不就无法产生一个大一个小的区间了嘛?
我们把这个问题转换一下,即为什么left和right相遇处的值一定小于keyi吗?
我们是让right先走的,这里我们分两种情况讨论:(如果是left先走的话就寄掉了)
1.right遇left,我们可以确保的一点是,right遇到left之前遇到的值都是比keyi的值大的,而left处的值又是小于keyi的,因此相遇时的值小于keyi。
2.left遇right, right先找到小的然后停下来了,之后left遇到它了,这个位置是比keyi处的值小的值。
2.2多趟过程的思想
当上面的单趟走完后,我们会发现,keyi左边的全是小于a[keyi]的,右边全是大于a[keyi]的。
现在我们不断的分区间,不断的重复刚刚的行为,就可以实现对整个数组的排序了,这是一个递归分治的典型。
现在我给大家画图来分析一下下面几趟的过程:
以左半边为例:
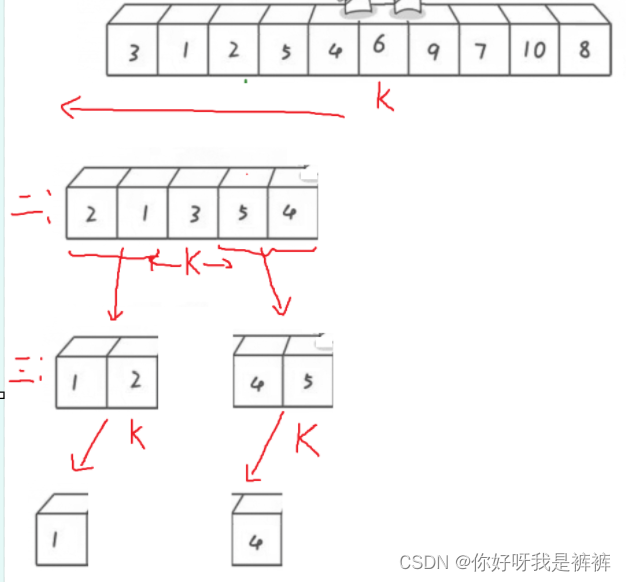
第二趟排序:
- 右边找小,找到3;左边找大,没找到,相遇了
- 交换2和3的位置
- 新的key为3
- 以k为基准,左右分区间
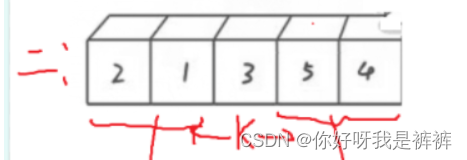
第三趟排序:
右边的找小直接遇到左,然后交换,新的key为2,下一个区间只有一个值。
第四趟排序:只有一个值了,我们可以返回了!
现在我们先不探究返回的条件,先将刚刚的思路完成
void qsort(int* a, int begin, int end)
{//keyi-->begin处的数据下标int keyi = begin;int left = begin;int right = end;while (left < right){//right先走,找小while(left < right && a[right] >= a[keyi]){--right;}//left再走,找大while(left < right&& a[left] <= a[keyi]){--left;}swap(&a[left], &a[right]);}keyi = left;// [begin, keyi-1]keyi[keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}那么,我们返回的条件如何判断呢?
我们在实现代码时可以发现,函数体里面是需要两个递归的,而我们需要探究的是递归的终止条件。
递归的终止条件是什么?就需要从传入的参数入手,这里我们将第三趟排序完成之后的两个递归图画出

在这里我们发现,递归的终止条件为begin>=end.
现在我们将代码补全:
void qsort(int* a, int begin, int end)
{if (begin >= end){return;}//keyi-->begin处的数据下标int keyi = begin;int left = begin;int right = end;while (left < right){//right先走,找小while(left < right && a[right] >= a[keyi]){--right;}//left再走,找大while(left < right&& a[left] <= a[keyi]){--left;}swap(&a[left], &a[right]);}keyi = left;// [begin, keyi-1]keyi[keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}至此,我们便完成了一次快速排序。
三.快排的优化
如果用上述的代码进行排序,假设我们要将一个数组排升序,而原数字是降序的话,那么我们的快速排序的时间复杂度就来到了O(n),这样的消耗是非常大的。
我们发现,这是因为key的值造成的,那么,如果我们可以控制让数组中的哪个数当key,是不是就可以解决问题了呢?
3.1随机数法选key
我们可以在数组下标中随便选一个数来当作我们的keyi,这就需要我们的rand函数。
int left = begin;int right = end;int randi = rand() % (right - left + 1);randi += left;Swap(&a[left], &a[randi]);int keyi = left;这里我们对第三行和第四行代码做出解释
第三行:如果一个数%99,那么它的结果是0-98;如果我们想要其的范围是0-99,则需要+1.
第四行:我们的left并不一定从最左边开始。
3.2三数取中选key
有的人觉得随机选数未免有些风险,就用了三数取中选key法,即找出数组最左边,最右边,以及中间的三个数,然后比较这三个数。谁的值是中位数,谁当key。
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] > a[right])//如果左大于右{if (a[right] > a[mid])//左大于右 右大于中 右为中位数return right;else if (a[mid] > a[left])//中大于左 左大于右 左为中位数return left;elsereturn mid;}else //a[right]>a[left] 右大于左{if (a[left] > a[mid]) 左大于中 左为中位数return left;else if (a[mid] > a[right]) 中大于右 右为中位数return right;elsereturn mid;}
}我们将选取k的代码改为下面这几行即可。
int midi = GetMidi(a, left, right);swap(&a[left], &a[midi]);int keyi = left;3.3小区间改造
由于快速排序是使用递归进行排序的,而每次递归都极大的占用空间,但其实我们的递归快到头的时候数组已经快有序了,这时我们再利用递归进行排序则会及大的占用栈的空间。
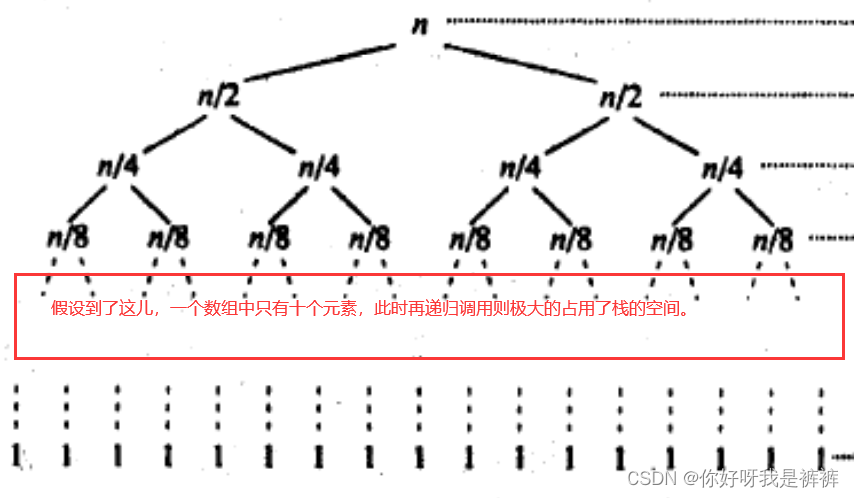
因此,我们在数组比较小的时候,直接换种排序即可,就譬如用插入排序。
void qsort(int* a, int begin, int end)
{if (begin >= end){return;}if (end - begin + 1 < 10)//数组中不足10个元素{InsertSort(a + begin, end - begin + 1);}else{int midi = GetMidi(a, begin, end);swap(&a[begin], &a[midi]);int keyi = begin;int left = begin;int right = end;while (left < right){//right先走,找小while (left < right && a[right] >= a[keyi]){--right;}//left再走,找大while (left < right && a[left] <= a[keyi]){--left;}swap(&a[left], &a[right]);}keyi = left;// [begin, keyi-1]keyi[keyi+1, end]qsort(a, begin, keyi - 1);qsort(a, keyi + 1, end);}
}四.挖坑法
上面的方法有些难理解,于是有人给出了一个理解起来比较容易的快排方法。
现在我们来理解一下这种挖坑法的算法思想。
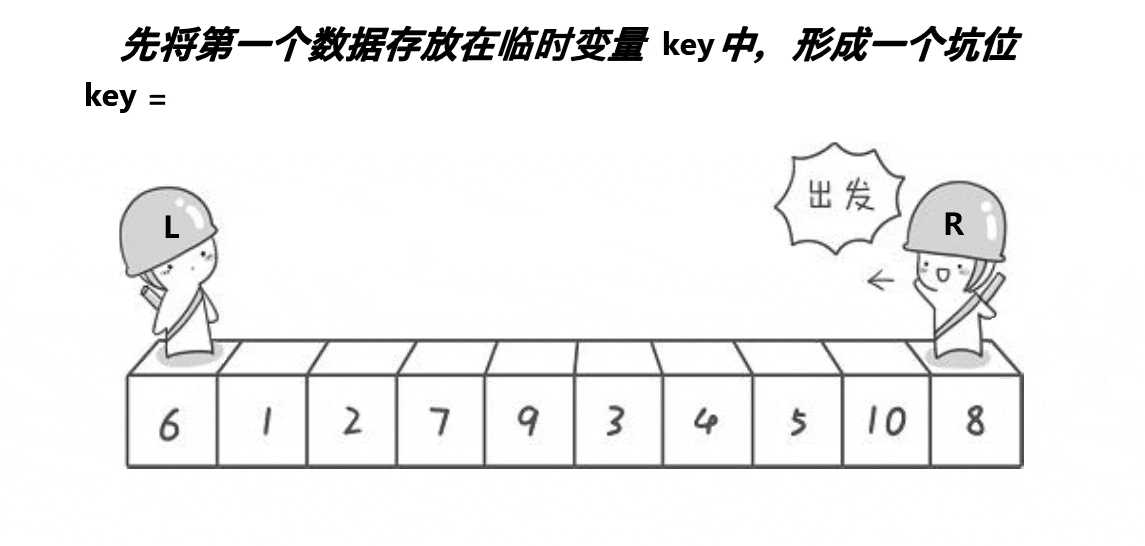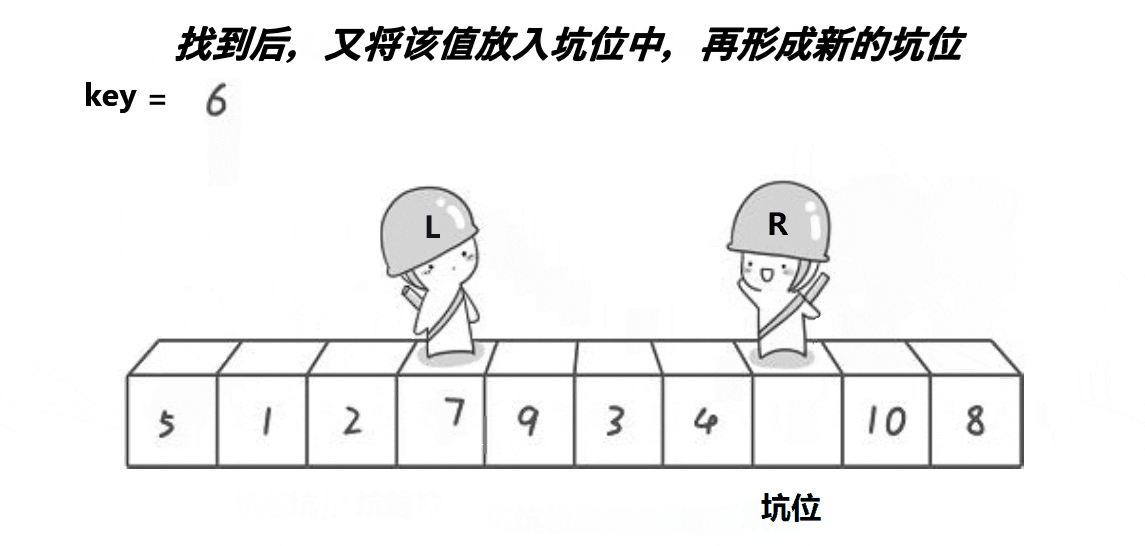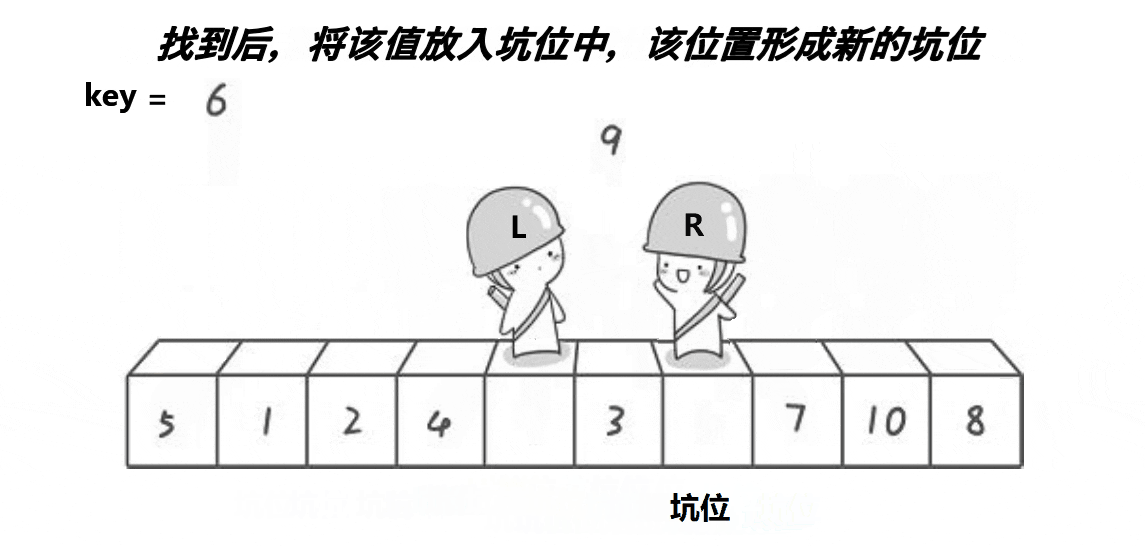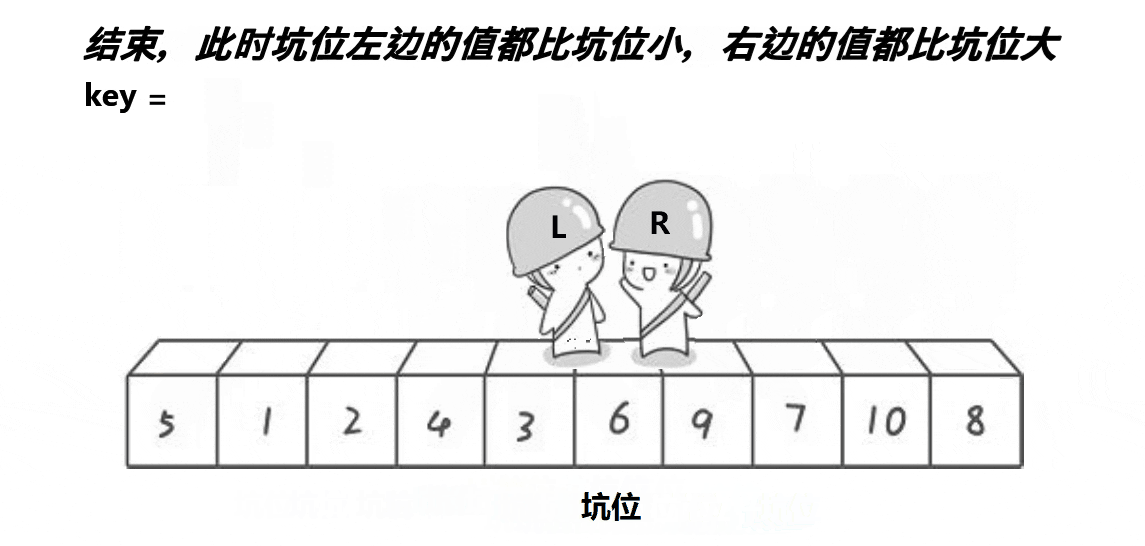
- 先将第一个数拿走,形成坑位,将此数定义为key
- 之后right先走,找小,找到了之后把数放到坑位中,right处形成新的坑
- left再走,找大,找到后将数放到坑位中,left处形成新的坑位
- 重复上述动作,直到两者相遇,将key放置在坑位。
void qsort(int* a, int begin, int end)
{if (begin >= end){return;}//记录坑位int piti = begin;//记录坑位的值int key = a[begin];int left = begin;int right = end;while (left < right){while (left < right && a[right] >= key){right--;}//放坑位,并更新坑位a[piti] = a[right];piti = right;while (left < right && a[left] <= key){left++;} a[piti] = a[left];piti = left;}a[piti] = key;qsort(a, begin, piti - 1);qsort(a, piti + 1, end);
}四.前后指针法
上面的方法效率比较低下,有一位大佬又发明了这么一个方法
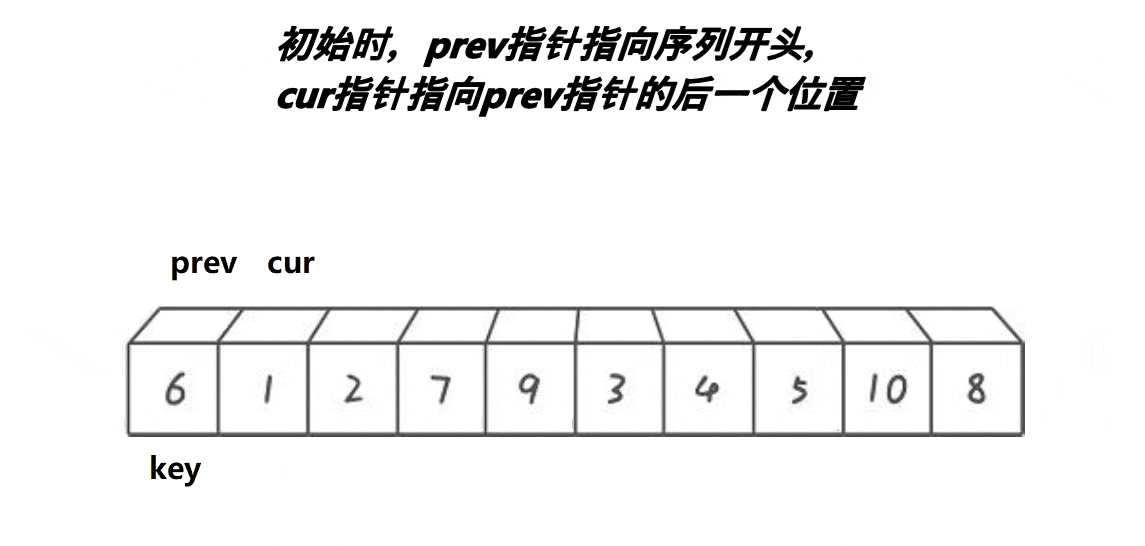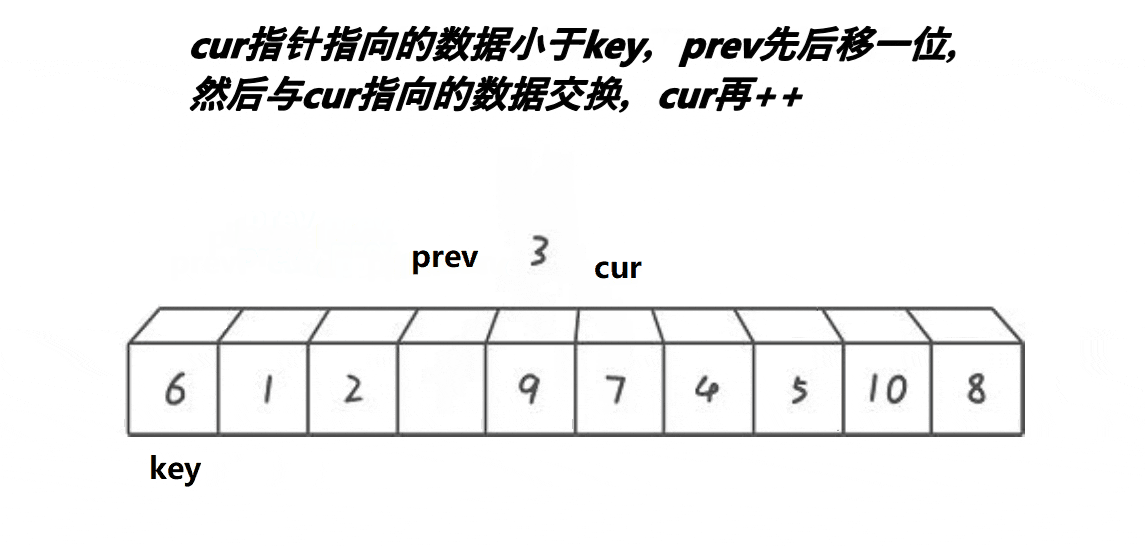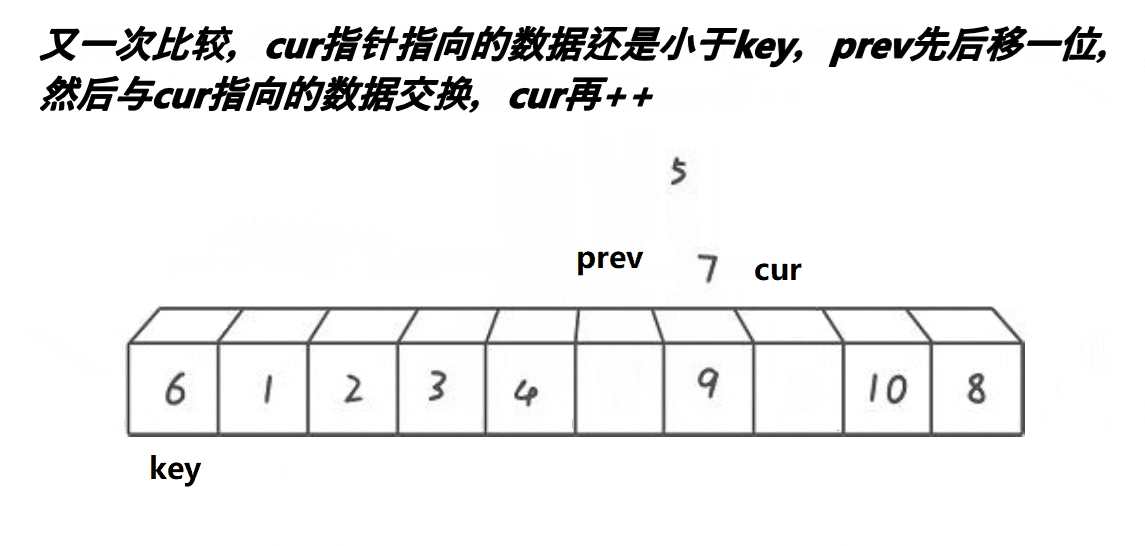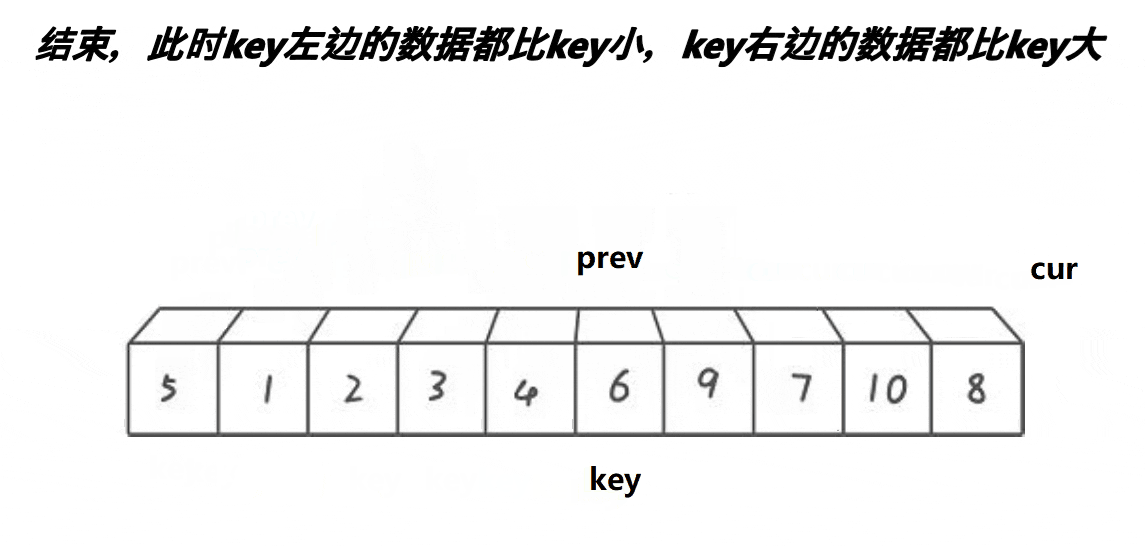
这个算法的思路是:
- 记录第一个位置为key
- 首先将prev置于第一个位置,cur置于第二个位置
- 判断cur处的值是否小于key,若小于,则prev先走一步,之后cur再走一步,若++prev!=cur,则将cur指向的内容和prev指向的内容交换,之后cur指针++
- 一直重复上一个动作,直到cur遇到的值大于key。
- 遇到的值大于key时,让cur往前走一步,prev不走。
- 等cur越界时,将prev和key的内容互换
- 此时key左边的值比key小,右边的值比key大。
这个思路的原理是:通过前后指针法,遇到大的则不让prev走,只让cur走。此时prev和cur中间就差了一个数,而这个数是大于key的,然后让cur再走,直到遇到小于key的值,此时prev和cur都走一步,prev处的值是第一个大于key的值,而此时cur的值是小于key的,让他们交换即可让大于key的值后移,小于key的值前移。而这两个数之间的值都是大于key的,重复上述动作直到cur越界.
void qsort(int* a, int left, int right)
{if (left >= right)return;int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){swap(&a[prev], &a[cur]);}++cur;}swap(&a[keyi], &a[prev]);qsort(a, left, keyi - 1);qsort(a, keyi + 1, right);
}为什么左边的小,右边的大?//结合代码理解
- 对于
prev指向的元素,它们都比基准元素大或等于基准元素。因为在遍历过程中,如果a[cur]比基准元素小,并且prev与cur不相等,则将a[cur]和a[prev]进行交换,将prev加1。如果a[cur]比基准元素大或等于基准元素,则不会进行交换操作,prev保持不变。 - 对于
cur指向的元素,它们都比基准元素小或等于基准元素。因为在遍历过程中,如果a[cur]比基准元素大,则不会进行交换操作,cur继续向后遍历。如果a[cur]比基准元素小,则与prev所指向的元素进行交换,并将prev加1。
六.利用栈将递归改非递归
因为函数栈帧是在栈(非数据结构上的栈)上开辟的,所以容易出现栈溢出的情况,为了解决这个问题,还可以将快速排序改为非递归版本,这样空间的开辟就在堆上了,堆上的空间比栈要多上许多。
为了实现快速排序的非递归版本,我们要借助我们以前实现的栈,来模拟非递归。
原理是:
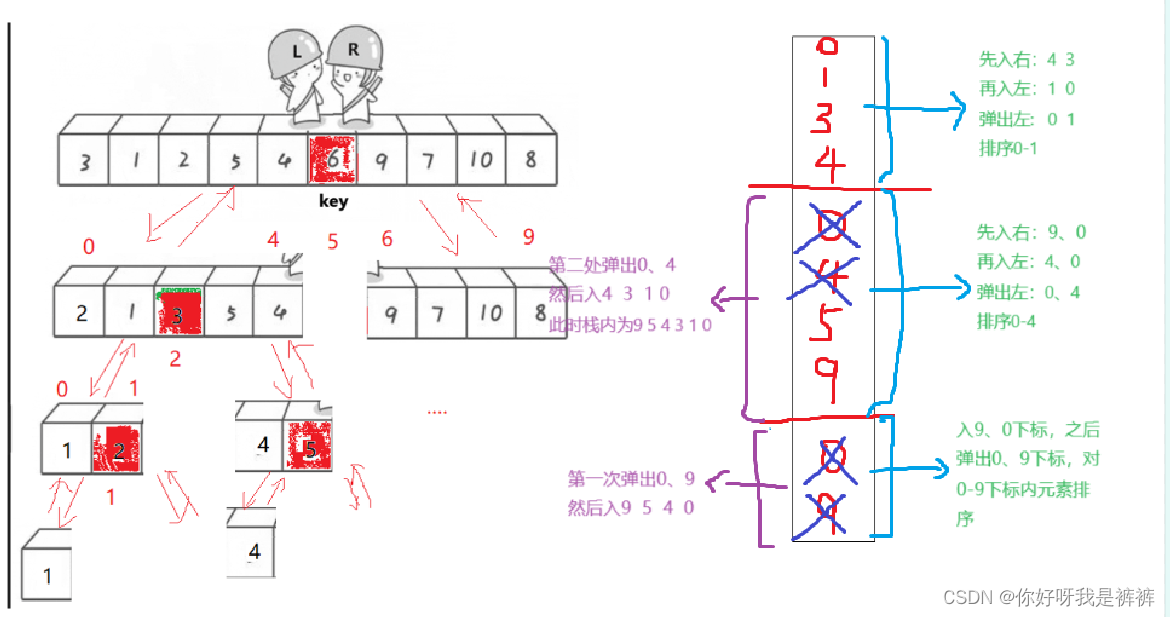
- 我们通过栈的先进后出的性质,先入一个左边的下标,再入一个右边的下标。
- 之后我们将它们弹出,并完成单趟排序。然后我们就可以得到了左区间和右区间。
- 我们先入右区间,再入左区间,以保证我们会先排序左区间再排序右区间。
- 之后再弹出两个,再排序一次,再入一次两个区间
- 一直循环这样的操作,一直到区间内没有元素为止。
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);//先入右,再入左STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){//先弹左int begin = STTop(&st);STPop(&st);//再弹右int end = STTop(&st);STPop(&st);// 单趟int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;// [begin, keyi-1] keyi [keyi+1, end] //先入右区间if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}//再入左区间if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);
}我现在来帮助大家画个图进行理解
后语
到此就结束了,下篇博客会更新归并排序的相关内容,希望大家持续关注,可以的话点个免费的赞或者评论关注一下啊!
贴一下专栏: 排序算法专栏 数据结构专栏
