98.验证二叉搜索树

·题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左

  子树

  只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

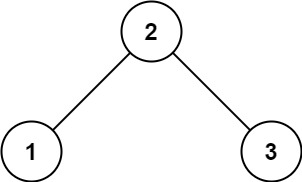
输入：root = [2,1,3]
输出：true

示例 2：

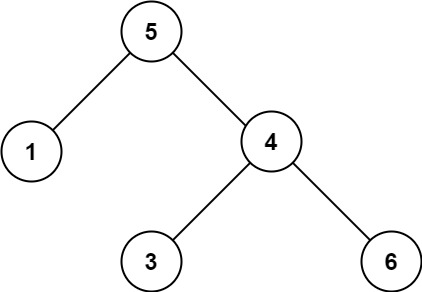
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

·解题思路

就是不能判断该节点和自己的左右子结点的大小，要判断左右子树的全部结点，因此需要引入两个指针min 和 max 来维护判断。

• 在这个调用中，val 是当前节点的值，被传递给右子树作为新的下界 lower。
  • 这意味着右子树中所有节点的值必须大于 val。
• upper 是右子树的上界，保持不变，因为右子树的所有节点还必须小于这个上界。

·Java代码

class Solution {public boolean isSymmetric(TreeNode root) {return dfs(root , null , null);}public boolean dfs(TreeNode node , Integer min , Integer max){if(node == null ) return true;int val = node. val ;if(min != null && val <= min) return false;if(max != null && val >= max) return false;if(!dfs(node.left , min , val)) return false;if(!dfs(node.right , val , max)) return false;return true;}public class TreeNode{int val;TreeNode left;TreeNode right;TreeNode(int x){val = x;}TreeNode(int val, TreeNode left, TreeNode right){this.val = val;this.left = left;this.right = right;}}
}