博客昵称:沈小农学编程
作者简介:一名在读硕士,定期更新相关算法面试题,欢迎关注小弟!
PS:哈喽!各位CSDN的uu们,我是你的小弟沈小农,希望我的文章能帮助到你。欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
题目难度:中等
默认优化目标:最小化时间复杂度。
Python默认为Python3。
目录
1 题目描述
2 题目解析
3 算法原理和代码实现
3.1 辅助数组
3.2 原地旋转
3.3 用翻转代替旋转
参考文献
1 题目描述
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
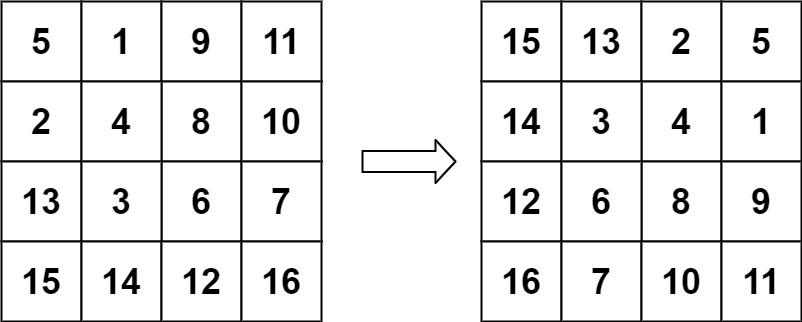
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
-
n == matrix.length == matrix[i].length -
1 <= n <= 20 -
-1000 <= matrix[i][j] <= 1000
2 题目解析
输入是一个n×n的矩阵matrix,输出是一个n×n的矩阵ans。约束条件是原地顺时针旋转90度。

3 算法原理和代码实现
3.1 辅助数组
可以创建一个二维数组ans作为辅助数组,将matrix中的数据以行的顺序依次存入ans的列中,最后再用ans更新matrix。
流程图如下所示:

时间复杂度为O(n^2),空间复杂度为O(n^2)。
C++代码实现
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n=matrix.size();auto ans=matrix;for(int i=0;i<n;i++){for(int j=0;j<n;j++){ans[j][n-i-1]=matrix[i][j];}}matrix=ans;}
};Python代码实现
class Solution:def rotate(self, matrix: List[List[int]]) -> None:n=len(matrix)ans=[[0]*n for _ in range(n)]
for i in range(n):for j in range(n):ans[j][n-i-1]=matrix[i][j]matrix[:]=ans3.2 原地旋转
我们现以matrix的四个顶点为例。左上顶点坐标为[i][j],右上顶点为[j][n-i-1],右下顶点为[n-i-1][n-j-1],左下顶点为[j][n-i-1]。可以用一个零时变量temp记录matrix[i][j],然后顺时针依次替换。我们把marix切分成如下形状。
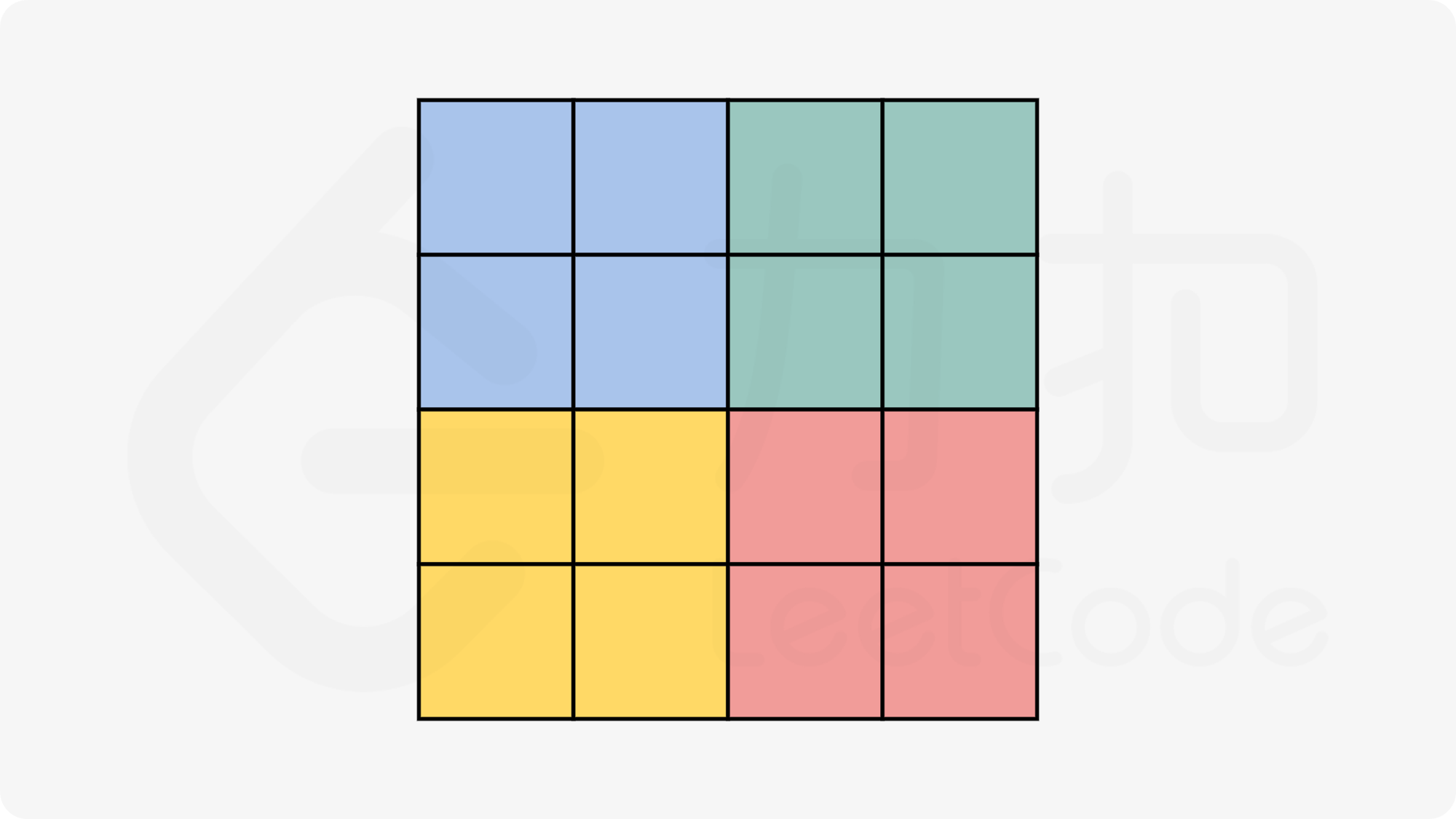
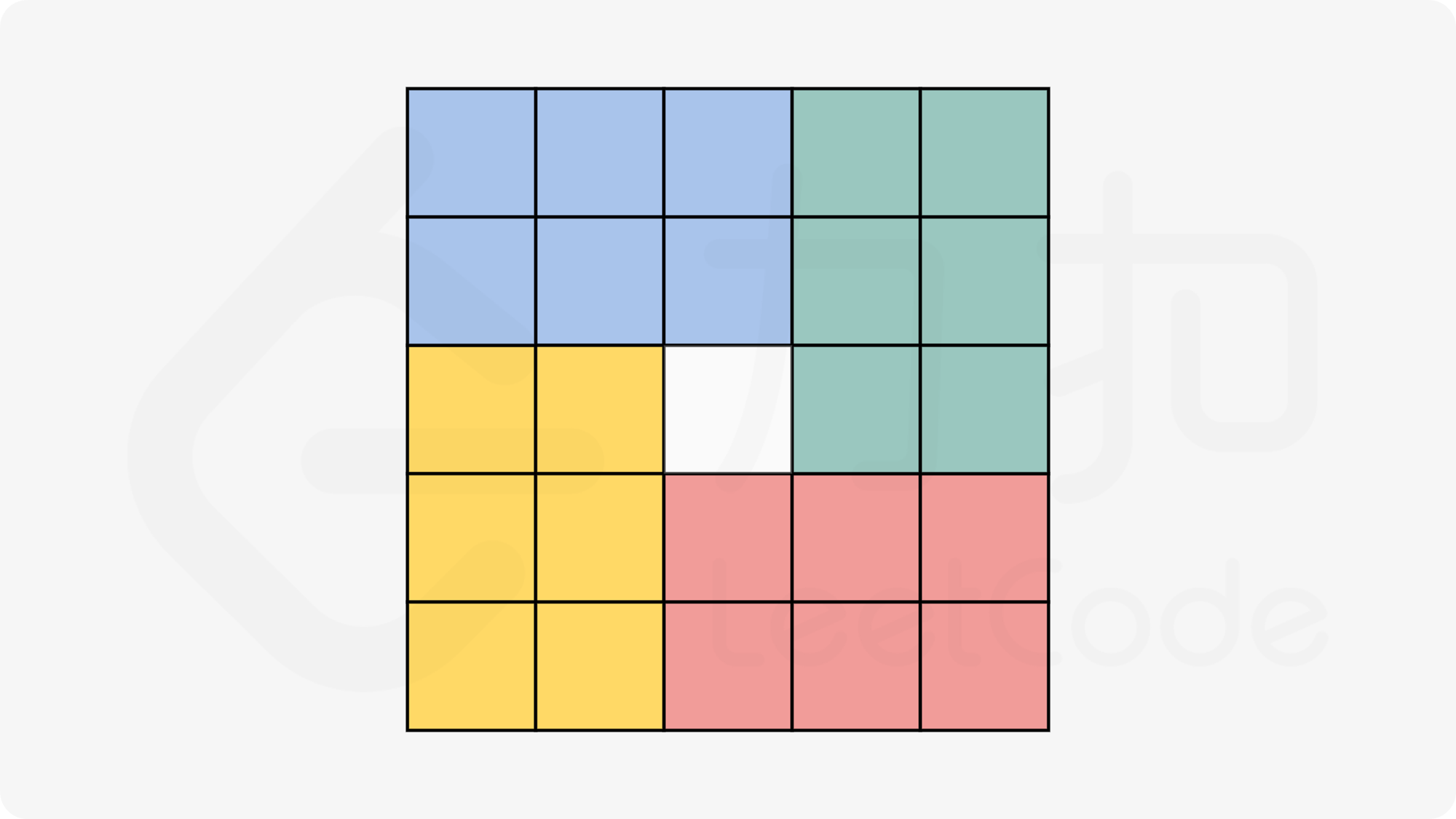
流程图如下所示:

时间复杂度为O(n^2),空间复杂度为O(1)。
C++代码实现
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n=matrix.size();for(int i=0;i<n/2;i++){for(int j=0;j<(n+1)/2;j++){int temp=matrix[i][j];matrix[i][j]=matrix[n-j-1][i];matrix[n-j-1][i]=matrix[n-1-i][n-j-1];matrix[n-i-1][n-j-1]=matrix[j][n-i-1];matrix[j][n-i-1]=temp;}}
}
};Python代码实现
class Solution:def rotate(self, matrix: List[List[int]]) -> None:n=len(matrix)for i in range(n//2):for j in range((n+1)//2):matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] \= matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]
3.3 用翻转代替旋转
用翻转代替旋转:先水平翻转,再对角线翻转。第一次从
第二次从
时间复杂度为O(n^2),空间复杂度为O(1)。
C++代码实现
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n=matrix.size();for(int i=0;i<n/2;i++){for(int j=0;j<n;j++){swap(matrix[i][j],matrix[n-i-1][j]); }
}for(int i=0;i<n;i++){for(int j=0;j<i;j++){swap(matrix[i][j],matrix[j][i]);}}
}
};Python代码实现
class Solution:def rotate(self, matrix: List[List[int]]) -> None:n=len(matrix)for i in range(n//2):for j in range(n):matrix[i][j],matrix[n-i-1][j]=matrix[n-i-1][j],matrix[i][j]for i in range(n):for j in range(i):matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]参考文献
力扣面试经典150题
力扣官方题解
