【Hot100】LeetCode—84. 柱状图中最大的矩形

---

• 原题链接：84. 柱状图中最大的矩形

---

1- 思路

• 观察是否可以扩展
  

单调栈

① 问题抽象：

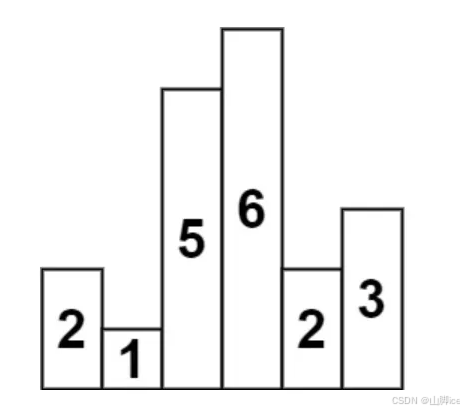
• 对于 1 找左边第一个比其小的元素，找右边第一个比其小的元素 ——> 找不到
  • 证明对于元素 1 来说其左右都可以扩展，扩展的宽度也就是数组的长度， 1 扩展的最大面积为 6
• 对于 5 而言，左边第一个比他小的元素是 1 ，右边第一个比他小的元素是 2
  • 则 5 可以扩展的区间为 (1,2)

② 具体实现

• 本题要求的是 左右第一个比当前元素小的元素，因此单调栈的顺序采用递减
• ① 结果收集 当当前元素 小于 单调栈栈口元素时候，就是收集结果的时候
  • mid（基准元素）： 栈口元素，当 当前元素 > st.peek() ，此时 mid = st.peek(), st.pop()
  • left（左侧第一个小的元素）：栈口元素的下一个，left = st.peek()
  • right（右侧第一个小的元素）：当前遍历的元素right = i

---

2- 实现

⭐84. 柱状图中最大的矩形——题解思路

class Solution {public int largestRectangleArea(int[] heights) {// 1. 头尾 加 0int[] newHeight = new int[heights.length+2];newHeight[0] = 0;newHeight[newHeight.length-1]=0;int index = 1;for(int i = 0 ;i < heights.length;i++){newHeight[index++] = heights[i];}heights = newHeight;// 2. 定义单调栈Stack<Integer> st = new Stack<>();st.push(0);int res = 0;for(int i = 1 ; i < heights.length;i++){if(heights[i] >= heights[st.peek()]){st.push(i);}else{while(heights[i] < heights[st.peek()]){int mid = st.peek();st.pop();int left = st.peek();int right = i;int width = right-left-1;int h = heights[mid];res = Math.max(res,h*width);}st.push(i);}}return res;}
}

---

3- ACM 实现

public class maxRectangle {public static int maxR(int[] heights) {// 1. 头尾 加 0int[] newHeight = new int[heights.length+2];newHeight[0] = 0;newHeight[newHeight.length-1]=0;int index = 1;for(int i = 0 ;i < heights.length;i++){newHeight[index++] = heights[i];}heights = newHeight;// 2. 定义单调栈Stack<Integer> st = new Stack<>();st.push(0);int res = 0;for(int i = 1 ; i < heights.length;i++){if(heights[i] >= heights[st.peek()]){st.push(i);}else{while(heights[i] < heights[st.peek()]){int mid = st.peek();st.pop();int left = st.peek();int right = i;int width = right-left-1;int h = heights[mid];res = Math.max(res,h*width);}st.push(i);}}return res;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);System.out.println("输入数组长度");int n = sc.nextInt();int[] nums = new int[n];for(int i = 0 ; i < n;i++){nums[i] = sc.nextInt();}System.out.println("结果是"+maxR(nums));}
}