Metal & Metamaterial optics
表面等离子体激元(Surface Plasmon Polariton, SPP)
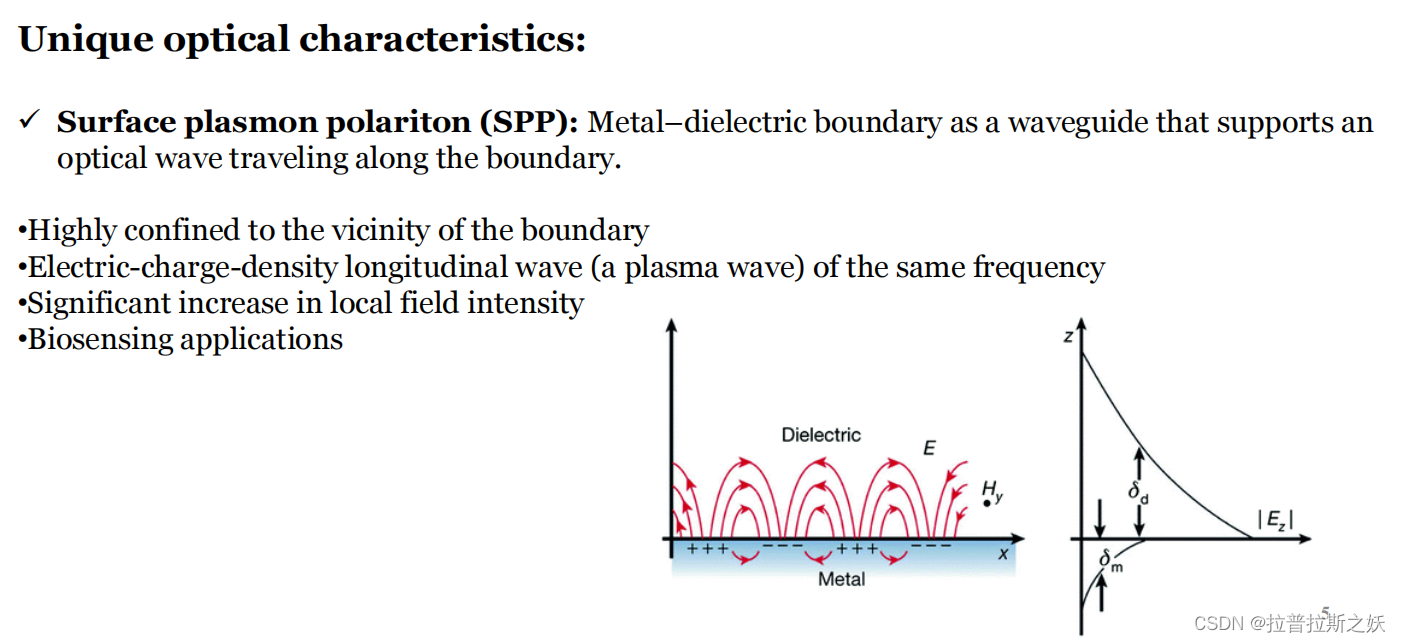
表面等离子体激元(Surface Plasmon Polaritons, SPPs)是在金属-介电边界处传播的光波导波。这种现象在金属与介电材料的交界面上产生,使光波沿着该边界传播。具体特点包括:
-
高度局限于边界附近
- SPPs具有高度局限性,光波被限制在金属-介电界面的极近处。这种局限性使得SPPs可以在亚波长尺度上操作光波。
-
电荷密度纵波
- SPPs不仅是光波的传播,还涉及相同频率的电荷密度纵波(即等离子波)。这些波在金属表面形成,通过激发金属自由电子的集体振荡产生。
-
局部场强度显著增加
- SPPs的另一个重要特点是局部场强度的显著增加。由于光波被高度局限在边界附近,其电磁场强度会大幅提升,从而产生更强的局部场效应。
-
生物传感应用
- 由于其高度敏感的局部场强度,SPPs在生物传感器领域有着广泛的应用。例如,SPPs可以用于检测生物分子与表面之间的相互作用,从而实现高灵敏度的生物传感。
图解分析
-
左图:SPP传播示意图
- 左侧的示意图展示了SPP在金属-介电边界的传播情况。红色波纹线表示电场分布(E),而黑色箭头表示磁场分布(Hy)。可以看出,电场主要集中在金属-介电边界附近,并沿着边界传播。
-
右图:场强度分布图
- 右侧的场强度分布图展示了电场(Ez)在金属和介电材料中的分布。可以看到,电场在介电材料(δd)和金属(δm)中的衰减程度不同。这种分布特点进一步强调了SPP波的局限性和高局部场强度。
局域表面等离子体(Localized Surface Plasmons, LSPs)
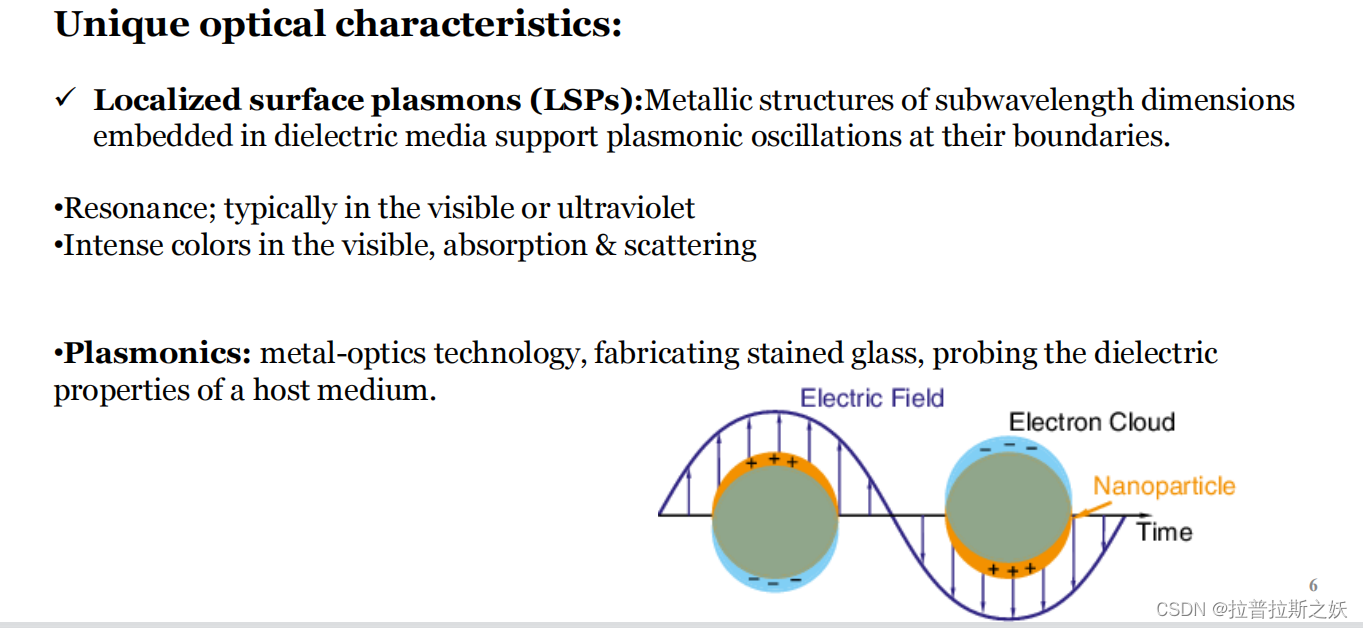
局域表面等离子体(Localized Surface Plasmons, LSPs)是在嵌入介电介质中的亚波长尺寸的金属结构边界上支持等离子体振荡的一种现象。LSPs具有以下几个关键特性:
-
共振现象
- LSPs通常在可见光或紫外光范围内发生共振。这意味着当入射光的频率与金属纳米结构的自然振荡频率相匹配时,会发生强烈的光-物质相互作用。
-
可见光中的强烈颜色
- 由于LSPs的共振效应,金属纳米结构会在可见光范围内显示出强烈的颜色。这种现象在吸收和散射光线时尤为显著。例如,中世纪的彩色玻璃就是通过掺入金属纳米颗粒来实现不同颜色的。
-
吸收和散射
- LSPs显著影响金属纳米颗粒的光学特性,导致强烈的光吸收和散射。这些特性使得LSPs在传感器和光学设备中具有重要应用。
图中展示了LSPs在纳米粒子表面的电场分布。可以看到,当电场(Electric Field)与纳米粒子相互作用时,会导致电子云(Electron Cloud)在粒子表面振荡。这个振荡是LSPs的核心机制,反映了金属纳米结构在电场中的响应。
不同的电容率(ε)和磁导率(μ)材料
电容率(ε)和磁导率(μ)特性
复数电容率(ε)的实部和虚部的物理意义
- 电容率的实部(Re{ε}) 表示材料的极化响应,决定了材料在电场下的位移和极化行为。
- 电容率的虚部(Im{ε}) 表示材料的能量损耗或增益,决定了材料如何吸收或放大电磁波的能量。
1. 电容率的实部(Re{ε})
公式:
ϵ = ϵ 0 ( 1 + χ ′ ) \epsilon = \epsilon_0 (1 + \chi') ϵ=ϵ0(1+χ′)
解释:
- ε:总电容率(复数)。
- ε₀:自由空间电容率,常数,约为8.854 × 10⁻¹² F/m。
- χ’:电容率的实部,称为电极化率(electric susceptibility)。
在这个公式中,电容率的实部(Re{ε})描述了材料在外加电场作用下的极化响应。这表示材料如何被极化,即内部电荷如何重新分布以对抗外部电场。具体来说:
- ε₀(1 + χ’) 表示在外部电场下,材料的电极化率对电场的响应。
- 当 χ’ > 0 时,材料被极化,并表现出比真空更高的电容率。
- 当 χ’ < 0 时,材料可能表现出不寻常的极化特性,如在一些特定的超材料中可能出现。
2. 电容率的虚部(Im{ε})
公式:
ϵ ′ ′ = ϵ 0 χ ′ ′ \epsilon'' = \epsilon_0 \chi'' ϵ′′=ϵ0χ′′
解释:
- ε’':电容率的虚部,也称为损耗因子(loss factor)。
- χ’':电容率的虚部,称为损耗极化率(loss susceptibility)。
这个公式描述了电容率的虚部(Im{ε}),它与材料的能量损耗或增益有关。具体来说:
- ε₀χ’’ 表示在交变电场下,材料的损耗特性。
- 当 χ’’ > 0 时,材料吸收电磁波的能量,表现为能量损耗。这种情况常见于导体和某些介质材料中。
- 当 χ’’ < 0 时,材料会对电磁波提供能量增益,这在某些有源材料或增益介质中可能出现。
磁导率(μ)为真实和正值
这一页的重点是讨论在磁导率(μ)为真实和正值的情况下,电容率(ε)的不同状态对波传播性质的影响。
1. 电容率(ε)为真实值
当电容率(ε)为真实值时:
- 无吸收或增益
- 在这种情况下,介质既不吸收能量也不增益能量。也就是说,电磁波在这种介质中传播时不会有能量损失或增加。
2. 电容率(ε)为复数值
当电容率(ε)为复数值时,情况会更加复杂,具体取决于其虚部(Im{ε})的符号:
-
吸收
- 如果Im{ε}(即ε″)为负值,则介质会吸收能量。此时,Re{ε}(即ε′)可以是正值或负值。
- 吸收情况的表达式如下:
- ϵ = ϵ 0 ( 1 + χ ′ ) \epsilon = \epsilon_0 (1 + \chi') ϵ=ϵ0(1+χ′)
- ϵ ′ ′ = ϵ 0 χ ′ ′ \epsilon'' = \epsilon_0 \chi'' ϵ′′=ϵ0χ′′
- 在这种情况下,复数电容率的虚部导致电磁波在介质中传播时能量被吸收,波的强度随传播距离衰减。
-
增益
- 如果Im{ε}(即ε″)为正值,则介质提供能量增益。此时,Re{ε}(即ε′)也可以是正值或负值。
- 增益情况的表达式与吸收情况类似,但虚部的符号相反:
- ϵ ′ ′ = ϵ 0 χ ′ ′ \epsilon'' = \epsilon_0 \chi'' ϵ′′=ϵ0χ′′
- 在这种情况下,复数电容率的虚部导致电磁波在介质中传播时能量增加,波的强度随传播距离增加。
电容率(ε)为真实和正值
当电容率(ε)为真实和正值时,磁导率(μ)的性质决定了波的传播特性:
- 电磁波的传播性质
- 磁导率(μ)决定了电磁波在介质中的传播行为。如果μ为正值,且ε也为正值,则介质通常是透明的,电磁波可以无损传播。
双正介质(DPS)、单负介质(SNG)和双负介质(DNG)分类
1. 双正介质(DPS: Double Positive Media)
- 定义: 双正介质是指电容率(ε)和磁导率(μ)均为正值的介质。
- 光学特性:
- 透明性: DPS介质通常是透明的,允许光线无障碍地通过。
- 正折射率: 这些介质具有正的折射率,这是传统光学材料的典型特征。
- 普通介电介质: 常见的介电材料如玻璃和水都属于DPS介质。
- 应用:
- DPS介质在日常光学器件中广泛应用,如透镜、窗户和光纤。
2. 单负介质(SNG: Single Negative Media)
- 定义: 单负介质是指电容率(ε)或磁导率(μ)中至少有一个为负值的介质。
- 光学特性:
- 不透明性: SNG介质通常是不透明的,光线无法直接通过。
- 支持光学表面波: 在与DPS材料的边界上,SNG介质可以支持光学表面波,这种波沿着边界传播,而不是穿透介质。
- 金属和铁氧体的特性:
- 金属在红外和可见光范围内表现出负电容率和正磁导率。
- 铁氧体在微波频率下表现出正电容率和负磁导率。
- 应用:
- SNG介质在电磁屏蔽和微波技术中有重要应用。
3. 双负介质(DNG: Double Negative Media)
- 定义: 双负介质是指电容率(ε)和磁导率(μ)均为负值的介质,也称为左手材料(left-handed media)。
- 光学特性:
- 透明性: 尽管DNG介质的电容率和磁导率均为负值,但它们依然可以是透明的。
- 负折射率: 这种介质具有负的折射率,意味着光线在这种介质中会以与普通介质相反的方向折射。
- 斯涅尔定律的反向: 在DPS-DNG边界上,斯涅尔定律导致负折射角。这种独特的性质使DNG介质在实现负折射和光学隐身中具有重要应用。
- 应用:
- DNG介质在光学隐身、超透镜和新型光学器件中具有潜在的应用。
DPS, SNG, DNG中的波传播
波矢定义
电磁波的基本方程:
k × H 0 = − ω ϵ E 0 \mathbf{k} \times \mathbf{H}_0 = -\omega \epsilon \mathbf{E}_0 k×H0=−ωϵE0
k × E 0 = ω μ H 0 \mathbf{k} \times \mathbf{E}_0 = \omega \mu \mathbf{H}_0 k×E0=ωμH0
波矢的定义:
k = ω ϵ μ k = \omega \sqrt{\epsilon \mu} k=ωϵμ
η = ω μ k = μ ϵ \eta = \frac{\omega \mu}{k} = \sqrt{\frac{\mu}{\epsilon}} η=kωμ=ϵμ
解释:
- k k k 是波矢的大小,表示波的传播常数。
- η \eta η 是介质的特性阻抗,表示电磁波在介质中的传播阻抗。
- 这些方程说明了波矢 k k k 和特性阻抗 η \eta η 是如何由介质的电磁性质决定的。
波矢的方向:
k \mathbf{k} k 垂直于 E \mathbf{E} E 和 H \mathbf{H} H 的平面,但其实际方向取决于 ϵ \epsilon ϵ 和 μ \mu μ 的符号。
解释:
- 波矢 k \mathbf{k} k 的方向决定了波的传播方向。
- 在SNG和DNG介质中,电容率( ϵ \epsilon ϵ)和磁导率( μ \mu μ)的符号可以改变波矢的方向,导致波的传播行为不同于普通介质。
复数波矢的定义:
k = β − j γ \mathbf{k} = \beta - j \gamma k=β−jγ
β − j γ = ω ϵ μ \beta - j \gamma = \omega \sqrt{\epsilon \mu} β−jγ=ωϵμ
解释:
- β \beta β 是波矢的实部,表示传播常数。
- γ \gamma γ 是波矢的虚部,表示衰减常数。
- 复数波矢 k \mathbf{k} k 包含了传播和衰减两部分信息,描述了波在介质中的传播和能量损耗特性。
DPS, SNG, DNG波传播相关参数
双正介质(DPS: Double Positive Medium)
- 定义: 双正介质是指电容率( ϵ \epsilon ϵ)和磁导率( μ \mu μ)均为正值的介质。
- 右手系统: 在这种介质中,波矢 k \mathbf{k} k 和阻抗 η \eta η 都是实数。
- k = ω ϵ μ k = \omega \sqrt{\epsilon \mu} k=ωϵμ
- η = ω μ k = μ ϵ \eta = \frac{\omega \mu}{k} = \sqrt{\frac{\mu}{\epsilon}} η=kωμ=ϵμ
- 传播特性: 在DPS介质中,电磁波可以正常传播,且没有显著的衰减。
单负介质(SNG: Single Negative Medium)
- 定义: 单负介质是指电容率( ϵ \epsilon ϵ)或磁导率( μ \mu μ)中至少有一个为负值的介质。
- 波矢和阻抗均为虚数:
- 由于 ϵ \epsilon ϵ 或 μ \mu μ 为负值,波矢 k \mathbf{k} k 和阻抗 η \eta η 都变为虚数。
- γ = ω ∣ ϵ ∣ ∣ μ ∣ \gamma = \omega \sqrt{|\epsilon||\mu|} γ=ω∣ϵ∣∣μ∣
- β = 0 \beta = 0 β=0
- η = j ∣ μ ∣ ∣ ϵ ∣ \eta = j \sqrt{\frac{|\mu|}{|\epsilon|}} η=j∣ϵ∣∣μ∣
解释:
- 当 β = 0 \beta = 0 β=0 时,单负介质不支持传播波,只有衰减波。
- 波的场强度随传播距离 z z z 指数衰减:
- exp ( − γ z ) \exp(-\gamma z) exp(−γz)
- 单负介质的典型表现是波的快速衰减,不支持长距离传播。
特性1:穿透深度或皮肤深度(Penetration depth or skin depth)
公式:
d p = 1 2 γ = λ 0 4 π ϵ 0 ∣ ϵ ∣ ∣ μ ∣ μ 0 d_p = \frac{1}{2\gamma} = \frac{\lambda_0}{4\pi} \sqrt{\frac{\epsilon_0}{|\epsilon|} \frac{|\mu|}{\mu_0}} dp=2γ1=4πλ0∣ϵ∣ϵ0μ0∣μ∣
解释:
- 穿透深度 d p d_p dp 是光强衰减到原始强度的 e − 1 e^{-1} e−1 的深度。
- 该公式表示光在单负介质中的衰减深度,反映了波在介质中的渗透能力。
- 穿透深度与材料的电容率和磁导率有关,数值越小,表明介质对电磁波的吸收越强。
特性2:虚数阻抗(Imaginary impedance)
公式:
η : π 2 phase shift \eta: \frac{\pi}{2} \text{ phase shift} η:2π phase shift
解释:
- 虚数阻抗导致电磁波在介质中传播时发生 π / 2 \pi/2 π/2 相位移。
- 这种相位移是由于电磁波在单负介质中传播时的能量损耗和相位变化引起的。
双负介质(DNG: Double Negative Medium)
- 定义: 双负介质是指电容率( ϵ \epsilon ϵ)和磁导率( μ \mu μ)均为负值的介质。
- 在这种介质中,波矢和阻抗的表现如下:
1. 波矢和折射率
公式:
k = ω ∣ ϵ ∣ ∣ μ ∣ k = \omega \sqrt{|\epsilon||\mu|} k=ω∣ϵ∣∣μ∣
β = n k 0 \beta = n k_0 β=nk0
n = − ∣ ϵ ∣ ∣ μ ∣ ϵ 0 μ 0 n = -\sqrt{\frac{|\epsilon||\mu|}{\epsilon_0 \mu_0}} n=−ϵ0μ0∣ϵ∣∣μ∣
解释:
- 由于 ϵ \epsilon ϵ 和 μ \mu μ 均为负值,波矢的定义使用了它们的绝对值。
- β \beta β 是传播常数,表示波的传播方向和速率。
- n n n 是介质的折射率,由于 ϵ \epsilon ϵ 和 μ \mu μ 为负值,导致 n n n 也为负值,这种特性在传统介质中是没有的。
- 负折射率 n n n 导致电磁波在DNG介质中的传播方向与常规介质相反,称为负折射现象。
2. 阻抗
公式:
η = ∣ μ ∣ ∣ ϵ ∣ \eta = \sqrt{\frac{|\mu|}{|\epsilon|}} η=∣ϵ∣∣μ∣
解释:
- 阻抗 η \eta η 表示介质对电磁波传播的阻力。
- 在DNG介质中,阻抗的计算也基于 ϵ \epsilon ϵ 和 μ \mu μ 的绝对值。
3. 电磁场分量的方向关系
方程:
k × H 0 = ω ∣ ϵ ∣ E 0 \mathbf{k} \times \mathbf{H}_0 = \omega |\epsilon| \mathbf{E}_0 k×H0=ω∣ϵ∣E0
k × E 0 = − ω ∣ μ ∣ H 0 \mathbf{k} \times \mathbf{E}_0 = -\omega |\mu| \mathbf{H}_0 k×E0=−ω∣μ∣H0
解释:
- 这些方程描述了电场( E 0 \mathbf{E}_0 E0)和磁场( H 0 \mathbf{H}_0 H0)与波矢( k \mathbf{k} k)之间的关系。
- 在DNG介质中,电磁场分量的方向关系与传统介质不同,这意味着在这种介质中,电场和磁场的方向与波的传播方向发生了反转。
- 这种特性相当于交换了电场和磁场的角色,这也是负折射现象的重要特征。
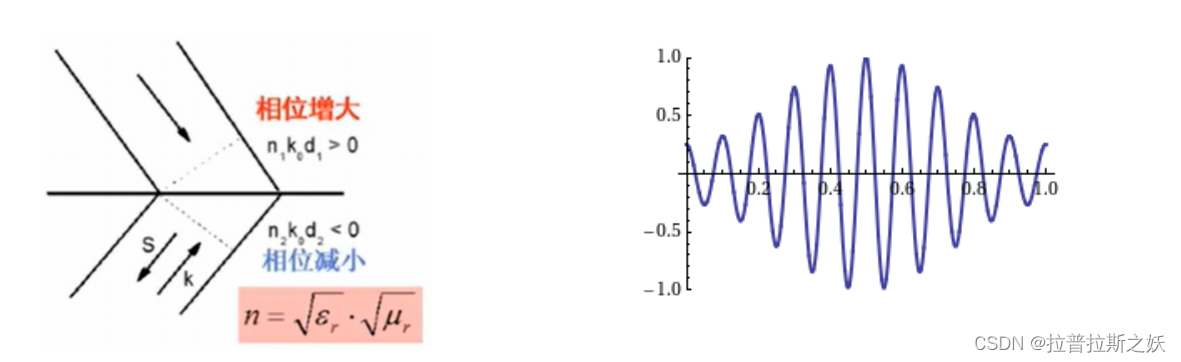
左图:电磁波在不同介质边界上的相位变化
- 上半部分(红色箭头)表示当电磁波从折射率 n 1 n_1 n1 和波矢 k 1 k_1 k1 的介质进入另一个介质时,如果满足 n 1 k 1 d 1 > 0 n_1 k_1 d_1 > 0 n1k1d1>0,则相位会增大。
- 下半部分(蓝色箭头)表示当电磁波从折射率 n 2 n_2 n2 和波矢 k 2 k_2 k2 的介质进入另一个介质时,如果满足 n 2 k 2 d 2 < 0 n_2 k_2 d_2 < 0 n2k2d2<0,则相位会减小。
- 在正折射率介质中,相位通常会增大,而在负折射率介质中,相位会减小。这是因为负折射率介质会使电磁波的传播方向发生反转。
右图:电磁波的波形图
- 在双负介质中,电磁波的波长、频率和相位都会受到介质特性的影响。
- 由于双负介质的负折射率,波形的传播方向和相位变化会与传统介质不同,导致波形的传播路径发生反转。
克拉默斯-克罗尼关系(Kramers-Kronig Relations)
负折射率材料在实现负折射的同时,必然伴随着一定的能量损耗。
- 原理: 当电容率或磁导率的实部为负时,其虚部不能为零。
- 意义: 这意味着在具有负折射率的介质中,吸收是不可避免的。负折射率通常伴随着吸收现象。
波矢 k \mathbf{k} k 的定义为:
k = β − j γ \mathbf{k} = \beta - j \gamma k=β−jγ
其中, β \beta β 是传播常数,表示电磁波的相位传播速度; γ \gamma γ 是衰减常数,表示电磁波在介质中的能量损耗。
电容率 ϵ \epsilon ϵ 和磁导率 μ \mu μ 均为复数:
ϵ = ϵ ′ + j ϵ ′ ′ \epsilon = \epsilon' + j\epsilon'' ϵ=ϵ′+jϵ′′
μ = μ ′ + j μ ′ ′ \mu = \mu' + j\mu'' μ=μ′+jμ′′
其中, ϵ ′ \epsilon' ϵ′ 和 μ ′ \mu' μ′ 是介质的储能特性(实部), ϵ ′ ′ \epsilon'' ϵ′′ 和 μ ′ ′ \mu'' μ′′ 是介质的损耗特性(虚部)。
根据复数波矢的定义和介质的复数参数,波矢的平方可以表示为:
k 2 = ( β − j γ ) 2 = ω 2 ( ϵ ′ + j ϵ ′ ′ ) ( μ ′ + j μ ′ ′ ) k^2 = (\beta - j\gamma)^2 = \omega^2 (\epsilon' + j\epsilon'')(\mu' + j\mu'') k2=(β−jγ)2=ω2(ϵ′+jϵ′′)(μ′+jμ′′)
为了匹配复数的实部和虚部:
− 2 β γ = ω 2 ( ϵ ′ μ ′ ′ + ϵ ′ ′ μ ′ ) -2\beta\gamma = \omega^2 (\epsilon'\mu'' + \epsilon''\mu') −2βγ=ω2(ϵ′μ′′+ϵ′′μ′)
虚部关系表明,负折射率材料在实现负折射的同时,必然伴随着一定的能量损耗。这是因为这些材料需要满足克拉默斯-克罗尼关系(Kramers-Kronig Relations),实部和虚部之间的因果关系使得损耗无法完全消除。当电容率和磁导率的虚部匹配时,波矢可以为负,表示负折射现象。
功率流(Power Flow)
公式:
Re { 1 2 E × H ∗ } \text{Re}\left\{\frac{1}{2} \mathbf{E} \times \mathbf{H}^*\right\} Re{21E×H∗}
E 0 = η H 0 \mathbf{E}_0 = \eta \mathbf{H}_0 E0=ηH0
解释:
- 功率流描述了电磁波在介质中的能量传输方向和大小。
- 在无源介质中,功率流的实部应为正,表示能量沿正方向传播。
虚数阻抗(Imaginary Impedance)
公式:
Re ( η ) positive for passive media and power flow must be in the +z direction \text{Re}(\eta) \text{ positive for passive media and power flow must be in the +z direction} Re(η) positive for passive media and power flow must be in the +z direction
解释:
- 虚数阻抗会导致相位变化,影响电磁波在介质中的传播。
双负介质(DNG)中实现左手性(负折射率)的必要和充分条件
- 充分条件: ϵ \epsilon ϵ 和 μ \mu μ 的实部均为负值是实现左手性的充分条件,但不是必要条件。
- 必要和充分条件: 要实现左手性,必须满足以下条件:
ϵ ′ ∣ ϵ ∣ + μ ′ ∣ μ ∣ < 0 \frac{\epsilon'}{|\epsilon|} + \frac{\mu'}{|\mu|} < 0 ∣ϵ∣ϵ′+∣μ∣μ′<0
推导过程:
负折射率材料(或左手性材料)具有一些与传统正折射率材料不同的独特性质,包括:
- 在负折射率材料中,电磁波的相位速度方向与能量流(即功率流)的方向相反。
- 相位速度由波矢 k \mathbf{k} k 的实部( β \beta β)决定,而能量流方向则由电场和磁场的交叉乘积决定。
-
β \beta β 和 γ \gamma γ 都为正值:
- 在实际物理系统中, β \beta β 和 γ \gamma γ 都需要为正值以表示实际的传播和衰减现象。
- β \beta β 为正值表示电磁波相位传播的正向传播,这对应于波前向前传播。
- γ \gamma γ 为正值表示能量的衰减,能量在介质中逐渐减少,这是实际材料中能量损耗的表现。
-
乘积为负值:
- 乘积为负值的要求源于负折射率材料的特性:
- 在负折射率材料中,电磁波的相位速度方向(由 β \beta β决定)和能量流方向相反。
- 为了实现这一点, β \beta β 和 γ \gamma γ 的乘积必须为负,这确保了波矢的虚部与实部之间的关系符合负折射率材料的特性。
- 乘积为负值的要求源于负折射率材料的特性:
波矢 k \mathbf{k} k 的平方可以表示为:
k 2 = ( β − j γ ) 2 = ω 2 ϵ μ k^2 = (\beta - j\gamma)^2 = \omega^2 \epsilon \mu k2=(β−jγ)2=ω2ϵμ
将复数电容率和磁导率代入公式,我们得到:
( β − j γ ) 2 = ω 2 ( ϵ ′ + j ϵ ′ ′ ) ( μ ′ + j μ ′ ′ ) (\beta - j\gamma)^2 = \omega^2 (\epsilon' + j\epsilon'')(\mu' + j\mu'') (β−jγ)2=ω2(ϵ′+jϵ′′)(μ′+jμ′′)
展开右边的表达式:
( β − j γ ) 2 = ω 2 [ ( ϵ ′ μ ′ − ϵ ′ ′ μ ′ ′ ) + j ( ϵ ′ μ ′ ′ + ϵ ′ ′ μ ′ ) ] (\beta - j\gamma)^2 = \omega^2 [(\epsilon'\mu' - \epsilon''\mu'') + j(\epsilon'\mu'' + \epsilon''\mu')] (β−jγ)2=ω2[(ϵ′μ′−ϵ′′μ′′)+j(ϵ′μ′′+ϵ′′μ′)]
匹配复数的虚部:
− 2 β γ = ω 2 ( ϵ ′ μ ′ ′ + ϵ ′ ′ μ ′ ) -2\beta\gamma = \omega^2 (\epsilon'\mu'' + \epsilon''\mu') −2βγ=ω2(ϵ′μ′′+ϵ′′μ′)
假设介质是无损耗的,即 ϵ ′ ′ = 0 \epsilon'' = 0 ϵ′′=0 和 μ ′ ′ = 0 \mu'' = 0 μ′′=0,我们得到:
− 2 β γ = ω 2 ( ϵ ′ ⋅ 0 + 0 ⋅ μ ′ ) = 0 -2\beta\gamma = \omega^2 (\epsilon' \cdot 0 + 0 \cdot \mu') = 0 −2βγ=ω2(ϵ′⋅0+0⋅μ′)=0
然而在实际介质中,损耗不可能完全为零,因此我们考虑虚部的存在。为了实现负折射率,要求:
ϵ ′ μ ′ ′ + ϵ ′ ′ μ ′ < 0 \epsilon'\mu'' + \epsilon''\mu' < 0 ϵ′μ′′+ϵ′′μ′<0
到这里其实已经推导完毕,接下来是标准化步骤:
我们将初始条件 ϵ ′ μ ′ ′ + ϵ ′ ′ μ ′ \epsilon'\mu'' + \epsilon''\mu' ϵ′μ′′+ϵ′′μ′ < 0 的每一项除以 ∣ ϵ ∣ ∣ μ ∣ |\epsilon||\mu| ∣ϵ∣∣μ∣:
ϵ ′ μ ′ ′ + ϵ ′ ′ μ ′ ∣ ϵ ∣ ∣ μ ∣ < 0 \frac{\epsilon'\mu'' + \epsilon''\mu'}{|\epsilon||\mu|} < 0 ∣ϵ∣∣μ∣ϵ′μ′′+ϵ′′μ′<0
ϵ ′ ∣ ϵ ∣ ⋅ μ ′ ′ ∣ μ ∣ + ϵ ′ ′ ∣ ϵ ∣ ⋅ μ ′ ∣ μ ∣ < 0 \frac{\epsilon'}{|\epsilon|} \cdot \frac{\mu''}{|\mu|} + \frac{\epsilon''}{|\epsilon|} \cdot \frac{\mu'}{|\mu|} < 0 ∣ϵ∣ϵ′⋅∣μ∣μ′′+∣ϵ∣ϵ′′⋅∣μ∣μ′<0
定义以下归一化参数:
ϵ r ′ = ϵ ′ ∣ ϵ ∣ , ϵ r ′ ′ = ϵ ′ ′ ∣ ϵ ∣ \epsilon_r' = \frac{\epsilon'}{|\epsilon|}, \quad \epsilon_r'' = \frac{\epsilon''}{|\epsilon|} ϵr′=∣ϵ∣ϵ′,ϵr′′=∣ϵ∣ϵ′′
μ r ′ = μ ′ ∣ μ ∣ , μ r ′ ′ = μ ′ ′ ∣ μ ∣ \mu_r' = \frac{\mu'}{|\mu|}, \quad \mu_r'' = \frac{\mu''}{|\mu|} μr′=∣μ∣μ′,μr′′=∣μ∣μ′′
将归一化参数代入原始条件:
ϵ r ′ ⋅ μ r ′ ′ + ϵ r ′ ′ ⋅ μ r ′ < 0 \epsilon_r' \cdot \mu_r'' + \epsilon_r'' \cdot \mu_r' < 0 ϵr′⋅μr′′+ϵr′′⋅μr′<0
为了简化表达式,我们注意到归一化参数的模为1:
ϵ r ′ 2 + ϵ r ′ ′ 2 = 1 \epsilon_r'^2 + \epsilon_r''^2 = 1 ϵr′2+ϵr′′2=1
μ r ′ 2 + μ r ′ ′ 2 = 1 \mu_r'^2 + \mu_r''^2 = 1 μr′2+μr′′2=1
在这种情况下,我们只考虑实部,因为归一化后,虚部对条件的影响被包含在实部中。于是,我们最终得到:
ϵ ′ ∣ ϵ ∣ + μ ′ ∣ μ ∣ < 0 \frac{\epsilon'}{|\epsilon|} + \frac{\mu'}{|\mu|} < 0 ∣ϵ∣ϵ′+∣μ∣μ′<0
DPS-SNG 边界的反射与表面波
临界角,全内反射和倏逝场(Evanescent Field)
临界角(Critical Angle)是光学中的一个重要概念。当光线从一种介质(如水)射向另一种具有更低折射率的介质(如空气)时,如果入射角大于某一特定角度,光线将完全反射回原介质,而不会进入第二种介质。这个特定角度就是临界角。
根据斯涅尔定律(Snell’s Law),临界角的计算公式为:
sin θ c = n 2 n 1 \sin \theta_c = \frac{n_2}{n_1} sinθc=n1n2
其中:
- θ c \theta_c θc 是临界角。
- n 1 n_1 n1 是光线在初始介质中的折射率。
- n 2 n_2 n2 是光线在第二介质中的折射率(且 n 1 > n 2 n_1 > n_2 n1>n2)。
当入射角 θ i \theta_i θi 大于临界角 θ c \theta_c θc 时,就会发生全内反射。
倏逝场(Evanescent Field)是指在波动(如电磁波)遇到界面时产生的一种非传播性的波。它的能量迅速衰减,并且局限在界面附近,不像普通的波那样在空间中传播。
特性:
- 快速衰减:倏逝场的强度随着距离从界面迅速减弱,通常指数级衰减。
- 局限性:倏逝场主要存在于波与介质界面的附近区域。
- 产生:倏逝场通常在全内反射条件下或在不连续介质边界处产生。
反射机制
-
反射机制:
- 当光遇到DPS介质(介电常数ε和磁导率μ均为正)与SNG介质(ε或μ为负)之间的边界时,会发生反射。
- 这种反射会在SNG介质中产生一个倏逝场。倏逝场是一种迅速衰减的场,不会传播到介质中,而是局限在边界上。
-
类似全内反射:
- 这种边界现象类似于全内反射,当光从高折射率介质进入低折射率介质时,如果入射角大于临界角,就会发生全内反射。
- 关键点:
- 大于临界角的入射角:就像全内反射一样,在DPS-SNG边界的反射在入射角大于临界角时显著。
- 与入射角无关:与传统反射不同,在DPS-SNG边界的反射可以在满足倏逝条件的情况下,不受入射角的限制。
在DPS-SNG边界的表面波
在DPS介质和SNG介质的边界上,表面波(尤其是表面等离激元,SPPs)可以传播。以下是详细的解释:
传播方式
- 表面波沿着边界传播,但在边界两侧表现为倏逝衰减。
- 这些波局限于界面附近,其强度随着离开边界的距离指数衰减。
在两种介质中的传播方程和亥姆霍兹方程
- 假设一个横磁(TM)波,其特征是磁场分量 H x H_x Hx、电场分量 ε y ε_y εy和另一个电场分量 E z E_z Ez:
- 对于 y > 0 y > 0 y>0(DPS介质),波可以描述为 exp ( − γ 1 y ) exp ( − j β z ) \exp(-\gamma_1 y) \exp(-j \beta z) exp(−γ1y)exp(−jβz)。
- 对于 y < 0 y < 0 y<0(SNG介质),波可以描述为 exp ( γ 2 y ) exp ( − j β z ) \exp(\gamma_2 y) \exp(-j \beta z) exp(γ2y)exp(−jβz)。
- 亥姆霍兹方程(Helmholtz equation)控制这些波的传播:
- − γ 1 2 + β 2 = ω 2 μ 1 ϵ 1 -\gamma_1^2 + \beta^2 = \omega^2 \mu_1 \epsilon_1 −γ12+β2=ω2μ1ϵ1
- − γ 2 2 + β 2 = ω 2 μ 2 ϵ 2 -\gamma_2^2 + \beta^2 = \omega^2 \mu_2 \epsilon_2 −γ22+β2=ω2μ2ϵ2
电场分量和连续性条件
在DPS-SNG边界处,电磁场的各分量需要满足连续性条件。
-
H x H_x Hx在两种介质中都是连续的,定义为 H 0 H_0 H0。
-
电场分量 E y E_y Ey:
- E y E_y Ey的幅值由下式表示:
E y = ( − β ω ϵ 1 ) H 0 在介质1(DPS)中 E_y = \left( -\frac{\beta}{\omega \epsilon_1} \right) H_0 \quad \text{在介质1(DPS)中} Ey=(−ωϵ1β)H0在介质1(DPS)中
E y = ( − β ω ϵ 2 ) H 0 在介质2(SNG)中 E_y = \left( -\frac{\beta}{\omega \epsilon_2} \right) H_0 \quad \text{在介质2(SNG)中} Ey=(−ωϵ2β)H0在介质2(SNG)中 - 位移电流密度 D y = ϵ E y D_y = \epsilon E_y Dy=ϵEy 的连续性必须满足。
- E y E_y Ey的幅值由下式表示:
-
电场分量 E z E_z Ez:
- E z E_z Ez的幅值由下式表示:
E z = ( − γ 1 j ω ϵ 1 ) H 0 在介质1(DPS)中 E_z = \left( -\frac{\gamma_1}{j \omega \epsilon_1} \right) H_0 \quad \text{在介质1(DPS)中} Ez=(−jωϵ1γ1)H0在介质1(DPS)中
E z = ( γ 2 j ω ϵ 2 ) H 0 在介质2(SNG)中 E_z = \left( \frac{\gamma_2}{j \omega \epsilon_2} \right) H_0 \quad \text{在介质2(SNG)中} Ez=(jωϵ2γ2)H0在介质2(SNG)中 - 这里, γ 1 \gamma_1 γ1和 γ 2 \gamma_2 γ2都是正值,并且需要 ϵ 1 \epsilon_1 ϵ1和 ϵ 2 \epsilon_2 ϵ2具有相反的符号,以满足边界条件。
- E z E_z Ez的幅值由下式表示:
-
连续性条件:
- 为了确保 E z E_z Ez在边界处是连续的,我们有:
γ 1 ϵ 1 = γ 2 ϵ 2 \frac{\gamma_1}{\epsilon_1} = \frac{\gamma_2}{\epsilon_2} ϵ1γ1=ϵ2γ2
- 为了确保 E z E_z Ez在边界处是连续的,我们有:
-
电场分量 E y E_y Ey 的反转:
- 在边界处,电场分量 E y E_y Ey 必须反转其符号。这意味着在边界两侧,电场的方向是相反的。
- 这种反转是由于表面存在表面电荷密度波所引起的,这是一种沿边界传播的电荷密度纵波(charge-density longitudinal wave)。
表面等离激元(SPP)(表面波)
在DPS-SNG边界处,表面等离激元(SPP)是一种高度局限于界面并沿界面传播的电磁波。SPP包含电荷密度波的成分,这使其能够在界面处产生强烈的电磁场增强效果。
- 表面等离激元(SPP)是电荷密度波和光波的组合。它们沿着金属-介质或DPS-SNG界面传播,并且高度局限于界面附近。
- SPP存在的条件是 ∣ ϵ 2 ∣ > ϵ 1 |\epsilon_2| > \epsilon_1 ∣ϵ2∣>ϵ1。这意味着SNG介质的介电常数的绝对值必须大于DPS介质的介电常数。
- 在DPS介质中的衰减系数 γ 1 \gamma_1 γ1 和在SNG介质中的衰减系数 γ 2 \gamma_2 γ2 分别为:
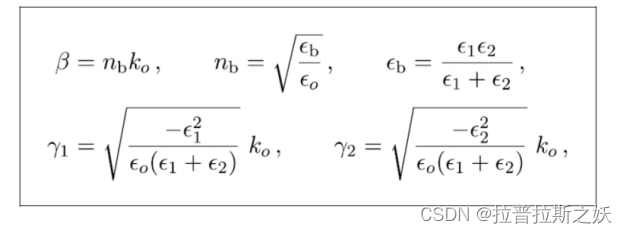
γ 1 = − ϵ 1 2 ϵ 0 ( ϵ 1 + ϵ 2 ) k 0 , γ 2 = − ϵ 2 2 ϵ 0 ( ϵ 1 + ϵ 2 ) k 0 \gamma_1 = \sqrt{\frac{-\epsilon_1^2}{\epsilon_0 (\epsilon_1 + \epsilon_2)}} k_0, \quad \gamma_2 = \sqrt{\frac{-\epsilon_2^2}{\epsilon_0 (\epsilon_1 + \epsilon_2)}} k_0 γ1=ϵ0(ϵ1+ϵ2)−ϵ12k0,γ2=ϵ0(ϵ1+ϵ2)−ϵ22k0 - 表面电荷密度波的存在可以通过以下关系式来描述:
β = n b k 0 , n b = ϵ b ϵ 0 , ϵ b = ϵ 1 ϵ 2 ϵ 1 + ϵ 2 \beta = n_b k_0, \quad n_b = \sqrt{\frac{\epsilon_b}{\epsilon_0}}, \quad \epsilon_b = \frac{\epsilon_1 \epsilon_2}{\epsilon_1 + \epsilon_2} β=nbk0,nb=ϵ0ϵb,ϵb=ϵ1+ϵ2ϵ1ϵ2
这里, β \beta β 是波矢的平行分量, k 0 k_0 k0 是真空中的波矢, ϵ 1 \epsilon_1 ϵ1 和 ϵ 2 \epsilon_2 ϵ2 分别是DPS和SNG介质的介电常数。
衡量表面波的指标
-
速度:
v = c 0 n b v = \frac{c_0}{n_b} v=nbc0
其中, c 0 c_0 c0 是光在真空中的速度, n b n_b nb 是等效折射率。 -
等离子体波长:
λ p = λ 0 n b \lambda_p = \frac{\lambda_0}{n_b} λp=nbλ0
这里, λ 0 \lambda_0 λ0 是真空中的波长, λ p \lambda_p λp 是等离子体波长。 -
消光系数:
γ 2 > γ 1 , by the factor ∣ ϵ 2 ∣ ϵ 1 \gamma_2 > \gamma_1, \quad \text{by the factor} \quad \frac{|\epsilon_2|}{\epsilon_1} γ2>γ1,by the factorϵ1∣ϵ2∣
消光系数描述了波在介质中的衰减程度。SNG介质中的衰减系数 γ 2 \gamma_2 γ2 大于DPS介质中的 γ 1 \gamma_1 γ1。 -
穿透深度:
d 2 = 1 2 γ 2 , d 1 = 1 2 γ 1 d_2 = \frac{1}{2\gamma_2}, \quad d_1 = \frac{1}{2\gamma_1} d2=2γ21,d1=2γ11
穿透深度表示波在介质中传播时,其强度降低到原来强度的1/e所需的距离。
例子8.1-1:SPP波的推导与分析

该例子探讨了在两个介质边界处支持的表面等离激元(SPP)波。以下是详细的推导和解释。
例子的基本参数
-
介电常数和磁导率:
- 两个介质具有相等的(正的)磁导率: μ 1 = μ 2 \mu_1 = \mu_2 μ1=μ2
- 介电常数分别为 ϵ 1 = 1.41 ϵ 0 \epsilon_1 = 1.41 \epsilon_0 ϵ1=1.41ϵ0 和 ϵ 2 = − 47 ϵ 0 \epsilon_2 = -47 \epsilon_0 ϵ2=−47ϵ0
-
自由空间波长:
- 自由空间波长 λ 0 = 1000 \lambda_0 = 1000 λ0=1000 nm
关键公式与推导
-
波矢的平行分量 β \beta β:
β = n b k 0 \beta = n_b k_0 β=nbk0
其中, n b n_b nb 是等效折射率, k 0 = 2 π λ 0 k_0 = \frac{2\pi}{\lambda_0} k0=λ02π 是真空中的波矢。 -
等效折射率 n b n_b nb 和等效介电常数 ϵ b \epsilon_b ϵb**:
n b = ϵ b ϵ 0 , ϵ b = ϵ 1 ϵ 2 ϵ 1 + ϵ 2 n_b = \sqrt{\frac{\epsilon_b}{\epsilon_0}}, \quad \epsilon_b = \frac{\epsilon_1 \epsilon_2}{\epsilon_1 + \epsilon_2} nb=ϵ0ϵb,ϵb=ϵ1+ϵ2ϵ1ϵ2
将已知的 ϵ 1 \epsilon_1 ϵ1 和 ϵ 2 \epsilon_2 ϵ2 代入,可以计算出 ϵ b \epsilon_b ϵb 和 n b n_b nb。 -
衰减系数 γ 1 \gamma_1 γ1 和 γ 2 \gamma_2 γ2:
γ 1 = − ϵ 1 2 ϵ 0 ( ϵ 1 + ϵ 2 ) k 0 , γ 2 = − ϵ 2 2 ϵ 0 ( ϵ 1 + ϵ 2 ) k 0 \gamma_1 = \sqrt{\frac{-\epsilon_1^2}{\epsilon_0 (\epsilon_1 + \epsilon_2)}} k_0, \quad \gamma_2 = \sqrt{\frac{-\epsilon_2^2}{\epsilon_0 (\epsilon_1 + \epsilon_2)}} k_0 γ1=ϵ0(ϵ1+ϵ2)−ϵ12k0,γ2=ϵ0(ϵ1+ϵ2)−ϵ22k0
这些公式描述了在DPS介质和SNG介质中波的衰减情况。
具体计算
-
计算等效折射率 n b n_b nb:
ϵ b = ϵ 1 ϵ 2 ϵ 1 + ϵ 2 = 1.41 ϵ 0 ⋅ ( − 47 ϵ 0 ) 1.41 ϵ 0 + ( − 47 ϵ 0 ) = − 66.27 ϵ 0 2 − 45.59 ϵ 0 ≈ 1.453 ϵ 0 \epsilon_b = \frac{\epsilon_1 \epsilon_2}{\epsilon_1 + \epsilon_2} = \frac{1.41 \epsilon_0 \cdot (-47 \epsilon_0)}{1.41 \epsilon_0 + (-47 \epsilon_0)} = \frac{-66.27 \epsilon_0^2}{-45.59 \epsilon_0} \approx 1.453 \epsilon_0 ϵb=ϵ1+ϵ2ϵ1ϵ2=1.41ϵ0+(−47ϵ0)1.41ϵ0⋅(−47ϵ0)=−45.59ϵ0−66.27ϵ02≈1.453ϵ0
n b = ϵ b ϵ 0 = 1.453 ϵ 0 ϵ 0 ≈ 1.206 n_b = \sqrt{\frac{\epsilon_b}{\epsilon_0}} = \sqrt{\frac{1.453 \epsilon_0}{\epsilon_0}} \approx 1.206 nb=ϵ0ϵb=ϵ01.453ϵ0≈1.206 -
计算等离子体波长:
λ p = λ 0 n b = 1000 nm 1.206 ≈ 829.4 nm \lambda_p = \frac{\lambda_0}{n_b} = \frac{1000 \text{ nm}}{1.206} \approx 829.4 \text{ nm} λp=nbλ0=1.2061000 nm≈829.4 nm -
计算衰减系数 γ 1 \gamma_1 γ1 和 γ 2 \gamma_2 γ2:
γ 1 = − ϵ 1 2 ϵ 0 ( ϵ 1 + ϵ 2 ) k 0 = − ( 1.41 ϵ 0 ) 2 ϵ 0 ( 1.41 ϵ 0 + ( − 47 ϵ 0 ) ) ⋅ 2 π λ 0 \gamma_1 = \sqrt{\frac{-\epsilon_1^2}{\epsilon_0 (\epsilon_1 + \epsilon_2)}} k_0 = \sqrt{\frac{-(1.41 \epsilon_0)^2}{\epsilon_0 (1.41 \epsilon_0 + (-47 \epsilon_0))}} \cdot \frac{2\pi}{\lambda_0} γ1=ϵ0(ϵ1+ϵ2)−ϵ12k0=ϵ0(1.41ϵ0+(−47ϵ0))−(1.41ϵ0)2⋅λ02π
γ 1 = − ( 1.41 ) 2 1.41 − 47 ⋅ 2 π 1000 nm = 1.9881 − 45.59 ⋅ 2 π 1000 nm ≈ 0.0436 ⋅ 2 π 1000 nm ≈ 0.208 ⋅ 2 π 1000 nm ≈ 1.306 × 1 0 − 3 nm − 1 \gamma_1 = \sqrt{\frac{-(1.41)^2}{1.41 - 47}} \cdot \frac{2\pi}{1000 \text{ nm}} = \sqrt{\frac{1.9881}{-45.59}} \cdot \frac{2\pi}{1000 \text{ nm}} \approx \sqrt{0.0436} \cdot \frac{2\pi}{1000 \text{ nm}} \approx 0.208 \cdot \frac{2\pi}{1000 \text{ nm}} \approx 1.306 \times 10^{-3} \text{ nm}^{-1} γ1=1.41−47−(1.41)2⋅1000 nm2π=−45.591.9881⋅1000 nm2π≈0.0436⋅1000 nm2π≈0.208⋅1000 nm2π≈1.306×10−3 nm−1
γ 2 = − ϵ 2 2 ϵ 0 ( ϵ 1 + ϵ 2 ) k 0 = − ( − 47 ϵ 0 ) 2 ϵ 0 ( 1.41 ϵ 0 + ( − 47 ϵ 0 ) ) ⋅ 2 π λ 0 \gamma_2 = \sqrt{\frac{-\epsilon_2^2}{\epsilon_0 (\epsilon_1 + \epsilon_2)}} k_0 = \sqrt{\frac{-(-47 \epsilon_0)^2}{\epsilon_0 (1.41 \epsilon_0 + (-47 \epsilon_0))}} \cdot \frac{2\pi}{\lambda_0} γ2=ϵ0(ϵ1+ϵ2)−ϵ22k0=ϵ0(1.41ϵ0+(−47ϵ0))−(−47ϵ0)2⋅λ02π
γ 2 = − 2209 ϵ 0 2 − 45.59 ϵ 0 ⋅ 2 π 1000 nm = 2209 45.59 ⋅ 2 π 1000 nm ≈ 48.48 ⋅ 2 π 1000 nm ≈ 6.96 ⋅ 2 π 1000 nm ≈ 0.0437 nm − 1 \gamma_2 = \sqrt{\frac{-2209 \epsilon_0^2}{-45.59 \epsilon_0}} \cdot \frac{2\pi}{1000 \text{ nm}} = \sqrt{\frac{2209}{45.59}} \cdot \frac{2\pi}{1000 \text{ nm}} \approx \sqrt{48.48} \cdot \frac{2\pi}{1000 \text{ nm}} \approx 6.96 \cdot \frac{2\pi}{1000 \text{ nm}} \approx 0.0437 \text{ nm}^{-1} γ2=−45.59ϵ0−2209ϵ02⋅1000 nm2π=45.592209⋅1000 nm2π≈48.48⋅1000 nm2π≈6.96⋅1000 nm2π≈0.0437 nm−1 -
计算穿透深度 d 1 d_1 d1 和 d 2 d_2 d2:
d 1 = 1 2 γ 1 ≈ 1 2 × 1.306 × 1 0 − 3 nm − 1 ≈ 381.1 nm d_1 = \frac{1}{2 \gamma_1} \approx \frac{1}{2 \times 1.306 \times 10^{-3} \text{ nm}^{-1}} \approx 381.1 \text{ nm} d1=2γ11≈2×1.306×10−3 nm−11≈381.1 nm
d 2 = 1 2 γ 2 ≈ 1 2 × 0.0437 nm − 1 ≈ 11.43 nm d_2 = \frac{1}{2 \gamma_2} \approx \frac{1}{2 \times 0.0437 \text{ nm}^{-1}} \approx 11.43 \text{ nm} d2=2γ21≈2×0.0437 nm−11≈11.43 nm
TM波和TE波在边界处的形成条件
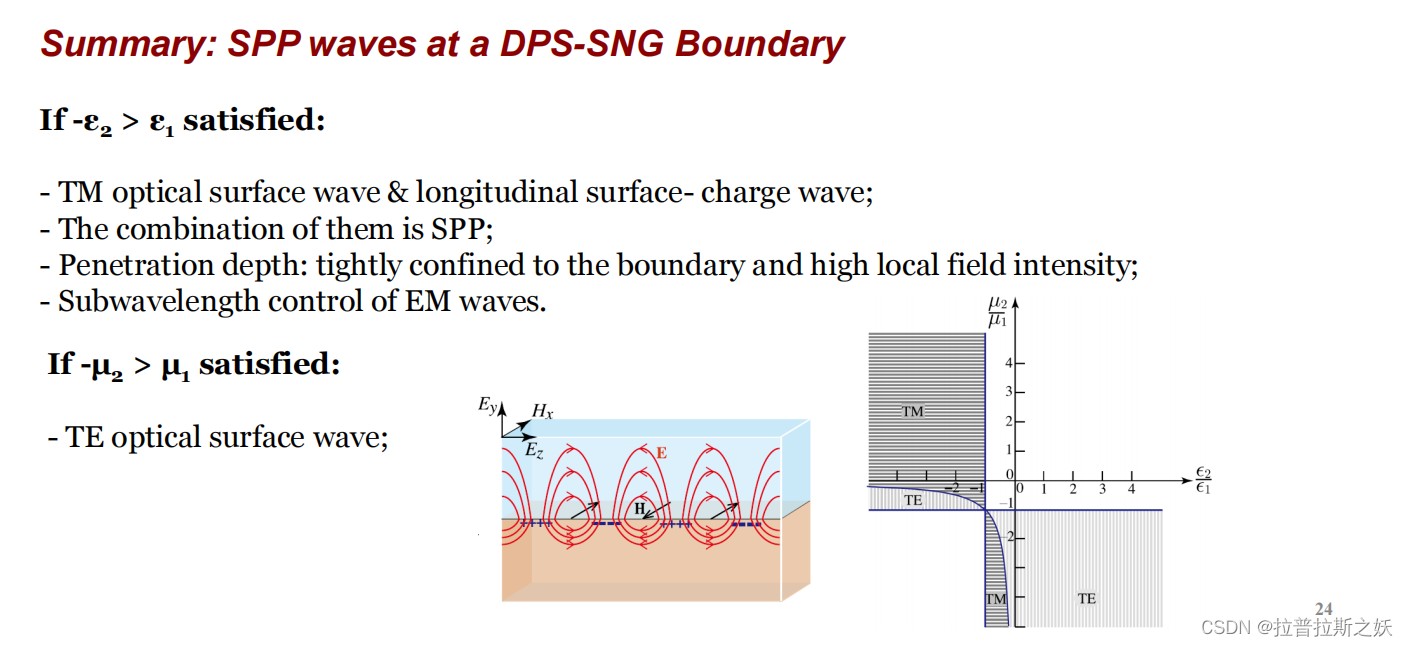
这一页重点强调了在DPS-SNG边界处不同条件下的表面波特性。TM波和TE波在边界处的形成条件不同,但都涉及到介电常数和磁导率的特定比值。
一、TM光学表面波(Transverse Magnetic Optical Surface Wave)
条件:-ε2 > ε1
-
TM光学表面波及纵向表面电荷波:
- TM波(横磁波)是一种光学表面波,电场主要在传播方向上。
- 纵向表面电荷波是一种电荷密度波,与光波同频。
-
SPP(表面等离子体极化子):
- SPP是TM光学表面波和纵向表面电荷波的组合。SPP在金属和介质边界处传播。
- SPP波在边界处高度局限,场强显著增强。
-
穿透深度和电磁波的亚波长控制:
- 穿透深度:SPP波紧密局限在边界处,具有高局部场强。
- 这种特性使得在亚波长尺度上控制电磁波成为可能。
二、TE光学表面波(Transverse Electric Optical Surface Wave)
条件:-μ2 > μ1
- TE光学表面波:
- TE波(横电波)是一种光学表面波,磁场主要在传播方向上。
DPS介质和有损SNG介质边界处,SPP波的传播和衰减特性。
这一页详细解释了在DPS介质和有损SNG介质边界处,SPP波的传播和衰减特性。通过引入复数介电常数,可以更加准确地描述有损介质中的能量耗散现象。
已知:
-
复数折射率表达式:
n b − j γ b k o = ϵ b ϵ o n_b - j\frac{\gamma_b}{k_o} = \sqrt{\frac{\epsilon_b}{\epsilon_o}} nb−jkoγb=ϵoϵb
这里, n b n_b nb 是有效折射率, γ b \gamma_b γb 是衰减系数, k o k_o ko 是自由空间波数。 -
衰减系数 α b \alpha_b αb:
α b = 2 γ b \alpha_b = 2\gamma_b αb=2γb
这是表示强度衰减的系数,决定了波在介质中传播时的能量损失。 -
传播长度 d b d_b db:
d b = 1 α b = 1 2 γ b d_b = \frac{1}{\alpha_b} = \frac{1}{2\gamma_b} db=αb1=2γb1
传播长度表示波在传播过程中强度减小到原来1/e的距离。 -
在边界两侧的穿透深度:
d 1 = 1 2 Re ( γ 1 ) , d 2 = 1 2 Re ( γ 2 ) d_1 = \frac{1}{2 \text{Re}(\gamma_1)}, \quad d_2 = \frac{1}{2 \text{Re}(\gamma_2)} d1=2Re(γ1)1,d2=2Re(γ2)1
这些公式表示在边界两侧的穿透深度,决定了波在不同介质中穿透的距离。
例子 8.1-2 复数SPP波: 金-氮化硅(Au-Si)界面上的表面SPP的传播特性
复数传播长度,折射率和衰减系数都可以通过有效介电常数计算

在自由空间波长 λ 0 = 1000 \lambda_0 = 1000 λ0=1000 nm 的情况下,氮化硅(Si 3 _3 3N 4 _4 4)和金(Au)的介电常数分别为:
- Si 3 _3 3N 4 _4 4: ϵ 1 = 1.41 ϵ 0 \epsilon_1 = 1.41 \epsilon_0 ϵ1=1.41ϵ0
- Au: ϵ 2 = ( − 47 + j 3.4 ) ϵ 0 \epsilon_2 = (-47 + j3.4) \epsilon_0 ϵ2=(−47+j3.4)ϵ0
其中 ϵ 0 \epsilon_0 ϵ0 是真空介电常数。
传播长度 d b d_b db 由复数介电常数 ϵ 2 \epsilon_2 ϵ2 的虚部决定,通过以下公式计算:
d b = 1 2 γ b = λ 0 4 π Im { ϵ b ϵ 0 } d_b = \frac{1}{2\gamma_b} = \frac{\lambda_0}{4\pi \text{Im}\left\{\sqrt{\frac{\epsilon_b}{\epsilon_0}}\right\}} db=2γb1=4πIm{ϵ0ϵb}λ0
有效介电常数 ϵ b \epsilon_b ϵb 由以下公式给出:
ϵ b = ϵ 1 ϵ 2 ϵ 1 + ϵ 2 \epsilon_b = \frac{\epsilon_1 \epsilon_2}{\epsilon_1 + \epsilon_2} ϵb=ϵ1+ϵ2ϵ1ϵ2
有效介电常数 ϵ b \epsilon_b ϵb 为:
ϵ b = − 66.27 + j 4.794 − 45.59 + j 3.4 ϵ 0 \epsilon_b = \frac{-66.27 + j4.794}{-45.59 + j3.4} \epsilon_0 ϵb=−45.59+j3.4−66.27+j4.794ϵ0
将这个分数转化为标准形式,得出:
ϵ b / ϵ 0 ≈ 1.453 + j 0.003234 \epsilon_b / \epsilon_0 \approx 1.453 + j0.003234 ϵb/ϵ0≈1.453+j0.003234
复数折射率 n b n_b nb 和衰减系数 γ b \gamma_b γb 的表达式为:
n b − j γ b k 0 = ϵ b ϵ 0 n_b - j\frac{\gamma_b}{k_0} = \sqrt{\frac{\epsilon_b}{\epsilon_0}} nb−jk0γb=ϵ0ϵb
有效介电常数 ϵ b \epsilon_b ϵb 的平方根计算如下:
1.453 + j 0.003234 ≈ 1.206 + j 0.001341 \sqrt{1.453 + j0.003234} \approx 1.206 + j0.001341 1.453+j0.003234≈1.206+j0.001341
因此:
n b = 1.206 n_b = 1.206 nb=1.206
γ b = 0.001341 k 0 \gamma_b = 0.001341 k_0 γb=0.001341k0
d b = 1 2 × 8.42 = 1 16.84 ≈ 0.0593 m m = 59.3 μ m d_b = \frac{1}{2 \times 8.42} = \frac{1}{16.84} \approx 0.0593 \, mm = 59.3 \, \mu m db=2×8.421=16.841≈0.0593mm=59.3μm
双正介质(DPS)和双负介质(DNG)边界处的负折射现象
通过利用负折射率材料,可以在近场和远场成像系统中实现亚波长分辨率。这些系统的设计必须考虑能量耗散和高频信息的恢复,以确保成像过程的高分辨率和高质量。负折射率材料的特殊性质使其能够有效地转换和恢复高频信息,突破传统光学系统的衍射极限,在纳米光学和超分辨率显微镜等领域具有广泛的应用前景。
负折射现象

负折射现象是双负介质的重要特性之一。这种现象的实现需要介质同时具有负的电容率(ε)和负的磁导率(μ)。在DPS-DNG边界处,负折射现象通过修改斯涅尔定律并考虑负折射率的特性得以解释。
斯涅尔定律描述了光波在两种介质界面处的折射行为,公式为:
n 1 sin θ 1 = n 2 sin θ 2 n_1 \sin \theta_1 = n_2 \sin \theta_2 n1sinθ1=n2sinθ2
对于负折射率 n 2 n_2 n2,斯涅尔定律修改为:
n 1 sin θ 1 = − ∣ n 2 ∣ sin θ 2 n_1 \sin \theta_1 = -|n_2| \sin \theta_2 n1sinθ1=−∣n2∣sinθ2
这意味着在负折射率介质中,折射角 θ 2 \theta_2 θ2 的符号是负的,即光波在介质边界的另一侧折射时会偏向入射光的相反方向。
相位匹配条件确保了在两种介质边界处,光波的相位保持连续。这对于实现负折射率材料的负折射现象至关重要。
图示部分分为两部分,分别展示了正折射和负折射的情况。
DNG透镜
- DNG材料的凸透镜表现为DPS材料的凹透镜:这意味着DNG材料的凸透镜会使平行光线向外发散,而不是像通常的凸透镜那样会聚光线。
- n 2 = − n 1 n_2 = -n_1 n2=−n1: 当介质2的折射率 n 2 n_2 n2 等于介质1的折射率 n 1 n_1 n1 的负值时,成像特性会发生变化。在这种情况下,成像是未倒像,并且放大倍数为1。这意味着物体在这种介质边界上的成像与物体大小一致且不翻转。
- ϵ 2 = − ϵ 1 and μ 2 = − μ 1 \epsilon_2 = -\epsilon_1 \quad \text{and} \quad \mu_2 = -\mu_1 ϵ2=−ϵ1andμ2=−μ1
当介质2的介电常数和磁导率分别为介质1的负值时,此时:
η 1 = μ 1 ϵ 1 and η 2 = μ 2 ϵ 2 \eta_1 = \sqrt{\frac{\mu_1}{\epsilon_1}} \quad \text{and} \quad \eta_2 = \sqrt{\frac{\mu_2}{\epsilon_2}} η1=ϵ1μ1andη2=ϵ2μ2
介质1和介质2的特征阻抗分别由其磁导率和介电常数决定。由于 ϵ 2 = − ϵ 1 \epsilon_2 = -\epsilon_1 ϵ2=−ϵ1 和 μ 2 = − μ 1 \mu_2 = -\mu_1 μ2=−μ1,特征阻抗关系保持不变。
满足成像条件,则:在DPS-DNG边界处,不发生反射现象,不论入射角度或光的偏振状态。这意味着所有入射光线在通过边界时都被完全折射,没有光线被反射回原介质。
负折射率材料边界处不发生反射现象,无论入射角度和光的偏振状态。这意味着光线能够完全进入材料,极大地减少了能量损失和成像误差。
负折射率材料(Negative Index Material, NIM)作为近场成像系统的原理
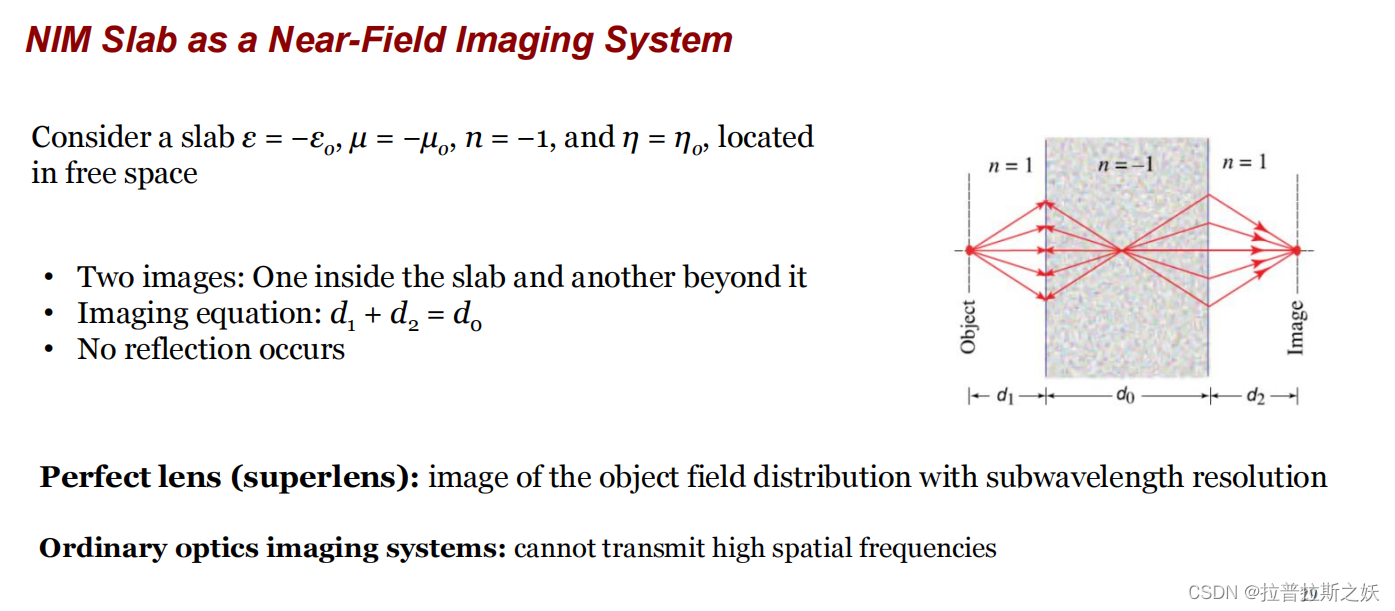
基本概念
考虑一个位于自由空间中的NIM板,其介电常数和磁导率分别为 ϵ = − ϵ 0 \epsilon = -\epsilon_0 ϵ=−ϵ0和 μ = − μ 0 \mu = -\mu_0 μ=−μ0,折射率为 n = − 1 n = -1 n=−1,特征阻抗为 η = η 0 \eta = \eta_0 η=η0。
成像特性
-
成像过程:
- 当光线通过这种NIM板时,会形成两个图像:一个在板内部,另一个在板的另一侧。
- 图像方程: d 1 + d 2 = d 0 d_1 + d_2 = d_0 d1+d2=d0,其中 d 1 d_1 d1是物体到板的距离, d 2 d_2 d2是板到图像的距离, d 0 d_0 d0是板的厚度。
- 在这种情况下,NIM板的折射率为-1,使得光线在通过板时发生反向偏转,形成未倒立的图像。
-
无反射现象:
- 在这种NIM板边界处,不发生反射现象,即所有入射光线都被完全折射通过板。
- 这种无反射现象不受入射角度和光的偏振状态影响。
完美透镜(Superlens)是指能够以亚波长分辨率成像的透镜。
傅里叶光学方法
傅里叶光学方法使用传递函数(Transfer Function)来描述光波在不同介质中的传播和变换。传递函数可以将复杂的光波传播过程简化为一系列数学运算,特别适用于描述在不同介质边界处的光波行为。
传递函数
传递函数 d 1 d_1 d1
传递函数 d 1 d_1 d1 表示光波在从物体到NIM板的距离 d 1 d_1 d1 处的传播行为:
H 1 ( ν x , ν y ) = exp ( − j k z d 1 ) H_1(\nu_x, \nu_y) = \exp(-jk_z d_1) H1(νx,νy)=exp(−jkzd1)
其中,
k z = k 0 2 − k x 2 − k y 2 = 2 π λ − 2 − ν x 2 − ν y 2 k_z = \sqrt{k_0^2 - k_x^2 - k_y^2} = 2\pi \sqrt{\lambda^{-2} - \nu_x^2 - \nu_y^2} kz=k02−kx2−ky2=2πλ−2−νx2−νy2
( ν x , ν y ) = ( k x 2 π , k y 2 π ) (\nu_x, \nu_y) = \left(\frac{k_x}{2\pi}, \frac{k_y}{2\pi}\right) (νx,νy)=(2πkx,2πky)
这里, k z k_z kz 是波矢的z分量, k 0 k_0 k0 是自由空间波矢, λ \lambda λ 是波长, ν x \nu_x νx 和 ν y \nu_y νy 是空间频率分量。
传递函数 d 0 d_0 d0
传递函数 d 0 d_0 d0 表示光波在NIM板内部的传播行为:
H 0 ( ν x , ν y ) = exp ( − j k z ′ d 0 ) H_0(\nu_x, \nu_y) = \exp(-jk'_z d_0) H0(νx,νy)=exp(−jkz′d0)
其中,
k z ′ = − k z k'_z = -k_z kz′=−kz
在NIM板内部,波矢的z分量取负值,表示光波在负折射率介质中的反向传播。
传递函数 d 2 d_2 d2
传递函数 d 2 d_2 d2 表示光波从NIM板到成像面的距离 d 2 d_2 d2 处的传播行为:
H 2 ( ν x , ν y ) = exp ( − j k z d 2 ) H_2(\nu_x, \nu_y) = \exp(-jk_z d_2) H2(νx,νy)=exp(−jkzd2)
系统传递函数
整体的系统传递函数可以表示为:
H = H 1 H 0 H 2 H = H_1 H_0 H_2 H=H1H0H2
空间频率的不同行为
一、低于 λ − 1 \lambda^{-1} λ−1的空间频率
当空间频率低于 λ − 1 \lambda^{-1} λ−1时,波矢的z分量 k z k_z kz 是实数:
k z = k 0 2 − k x 2 − k y 2 = 2 π λ − 2 − ν x 2 − ν y 2 k_z = \sqrt{k_0^2 - k_x^2 - k_y^2} = 2\pi \sqrt{\lambda^{-2} - \nu_x^2 - \nu_y^2} kz=k02−kx2−ky2=2πλ−2−νx2−νy2
在这种情况下,所有传递函数都是相位因子:
H 1 ( ν x , ν y ) = exp ( − j k z d 1 ) H_1(\nu_x, \nu_y) = \exp(-jk_z d_1) H1(νx,νy)=exp(−jkzd1)
H 0 ( ν x , ν y ) = exp ( − j k z ′ d 0 ) H_0(\nu_x, \nu_y) = \exp(-jk'_z d_0) H0(νx,νy)=exp(−jkz′d0)
H 2 ( ν x , ν y ) = exp ( − j k z d 2 ) H_2(\nu_x, \nu_y) = \exp(-jk_z d_2) H2(νx,νy)=exp(−jkzd2)
二、高于 λ − 1 \lambda^{-1} λ−1的空间频率
当空间频率高于 λ − 1 \lambda^{-1} λ−1时,波矢的z分量 k z k_z kz 是虚数:
k z = k 0 2 − k x 2 − k y 2 = − j 2 π ν x 2 + ν y 2 − λ − 2 k_z = \sqrt{k_0^2 - k_x^2 - k_y^2} = -j2\pi \sqrt{\nu_x^2 + \nu_y^2 - \lambda^{-2}} kz=k02−kx2−ky2=−j2πνx2+νy2−λ−2
在这种情况下,传递函数的表现是:
H 1 ( ν x , ν y ) = exp ( − γ d 1 ) H_1(\nu_x, \nu_y) = \exp(-\gamma d_1) H1(νx,νy)=exp(−γd1)
H 2 ( ν x , ν y ) = exp ( − γ d 2 ) H_2(\nu_x, \nu_y) = \exp(-\gamma d_2) H2(νx,νy)=exp(−γd2)
H 0 ( ν x , ν y ) = exp ( + γ d 0 ) H_0(\nu_x, \nu_y) = \exp(+\gamma d_0) H0(νx,νy)=exp(+γd0)
这里, γ \gamma γ 是衰减系数:
γ = 2 π ν x 2 + ν y 2 − λ − 2 \gamma = 2\pi \sqrt{\nu_x^2 + \nu_y^2 - \lambda^{-2}} γ=2πνx2+νy2−λ−2
图示解析
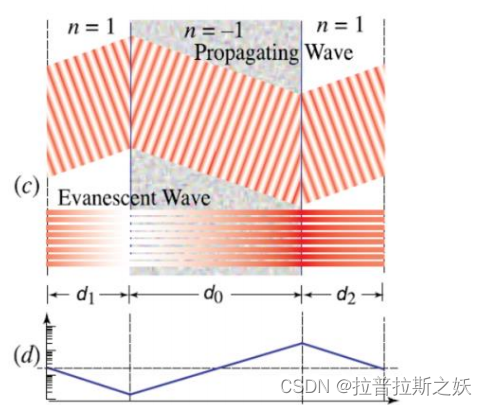
图示右侧展示了在NIM板中的光波传播路径,以及不同空间频率下的传播行为。
© 图示
-
传播波(Propagating Wave)和倏逝波(Evanescent Wave):
- 当空间频率低于 λ − 1 \lambda^{-1} λ−1时,光波在NIM板中作为传播波传播。
- 当空间频率高于 λ − 1 \lambda^{-1} λ−1时,光波在NIM板中作为倏逝波传播,迅速衰减。
-
光波路径:
光波从物体发出,经过距离 d 1 d_1 d1 传播到NIM板,然后在NIM板内部传播距离 d 0 d_0 d0,最后从NIM板传播距离 d 2 d_2 d2 到成像面。
(d) 图示
- 空间频率响应:
展示了系统对不同空间频率成分的响应。对于低于 λ − 1 \lambda^{-1} λ−1的空间频率,系统传递函数的相位因子起主要作用。对于高于 λ − 1 \lambda^{-1} λ−1的空间频率,系统传递函数的衰减因子起主要作用,导致高频信息的衰减。
负折射率材料(NIM)实现亚波长分辨率的近场和远场成像
能量耗散会阻碍成像过程中的信息恢复,特别是高空间频率成分的恢复。为了实现高分辨率成像,必须尽量减少能量耗散,这对于近场成像系统尤为重要。
近场成像系统
为了实现亚波长分辨率的近场成像系统,系统中的各个距离 d 1 d_1 d1、 d 0 d_0 d0 和 d 2 d_2 d2 必须相对于波长而言较小,尤其是在空间频率很高的情况下。这些距离小意味着光波在介质中的传播路径较短,从而减少了高频信息的损失。
远场成像系统
在远场成像系统中,倏逝波(Evanescent Waves)需要转换为传播波(Propagating Waves),以便在远场成像中恢复高频信息。通过负折射率材料,可以实现这种转换,从而在远场成像中保持高分辨率。
光各向异性介质光学
折射率椭球(Index Ellipsoid)
在光学中,材料的各向异性特性对光的传播有重要影响。各向异性介质的光学特性可以通过一个数学描述,即折射率椭球(Index Ellipsoid)来完全表示。
折射率椭球是用来描述各向异性介质中光的传播特性的数学工具。它的基本方程为:
x 1 2 n 1 2 + x 2 2 n 2 2 + x 3 2 n 3 2 = 1 \frac{x_1^2}{n_1^2} + \frac{x_2^2}{n_2^2} + \frac{x_3^2}{n_3^2} = 1 n12x12+n22x22+n32x32=1
这个方程表示的是一个三维空间中的椭球,其中 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3 是空间坐标,而 n 1 , n 2 , n 3 n_1, n_2, n_3 n1,n2,n3 分别是介质在不同方向上的折射率。通过这个椭球,可以直观地看到在不同方向上光的传播速度如何变化。
各向异性介质的分类
-
单轴晶体(Uniaxial Crystal):
- 单轴晶体的折射率椭球是一个旋转椭球(ellipsoid of revolution)。
- 在这种介质中,有一个光轴(光轴是一个特殊方向,在这个方向上光的折射率不同于其他方向)。
-
各向同性介质(Isotropic Medium):
- 各向同性介质的折射率椭球是一个球体(sphere)。
- 这种介质在所有方向上的折射率相同,即光在任何方向上传播时速度一致。
-
双轴晶体(Biaxial Crystals):
- 对于更复杂的双轴晶体,折射率椭球不是旋转对称的,而是一个三轴椭球,每个方向上的折射率都不同。
单轴晶体
单轴晶体是一类重要的各向异性材料,它们在光学中具有广泛的应用。单轴晶体的光学特性可以通过它们的波矢面(k surface)方程来描述,这在理解光在这些材料中的传播行为中起到了关键作用。
波矢面方程(Equation of the k Surface)
波矢面方程描述了光波矢在单轴晶体中的分布情况。它的形式如下:
( k 2 − n o 2 k o 2 ) ( k 1 2 + k 2 2 n e 2 + k 3 2 n o 2 − k o 2 ) = 0 (k^2 - n_o^2 k_o^2) \left( \frac{k_1^2 + k_2^2}{n_e^2} + \frac{k_3^2}{n_o^2} - k_o^2 \right) = 0 (k2−no2ko2)(ne2k12+k22+no2k32−ko2)=0
这里:
- k k k 是总波矢。
- k o k_o ko 是真空中的波矢。
- n o n_o no 是普通光折射率。
- n e n_e ne 是 extraordinary 光折射率。
- k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3 分别是波矢在三个坐标轴上的分量。
这个方程的解有两个部分:一个球面和一个旋转椭球。
两个解(Two Solutions)
波矢面方程有两个解,分别对应于不同的光传播模式:
-
球面解:
- 对应于普通光(ordinary ray),其波矢满足:
k = n o k o k = n_o k_o k=noko - 表示在各个方向上的传播速度相同,折射率 n o n_o no 是常数。
- 对应于普通光(ordinary ray),其波矢满足:
-
旋转椭球解:
- 对应于 extraordinary 光,其波矢满足:
k 1 2 + k 2 2 n e 2 + k 3 2 n o 2 = k o 2 \frac{k_1^2 + k_2^2}{n_e^2} + \frac{k_3^2}{n_o^2} = k_o^2 ne2k12+k22+no2k32=ko2 - 表示在不同方向上的传播速度不同,折射率 n n n 是方向依赖的。
- 对应于 extraordinary 光,其波矢满足:
普通光(ordinary ray)和 extraordinary 光
当光进入单轴晶体时,会分裂成普通光和extraordinary 光两束,且它们的传播方向不同,导致双折射效应。
- 普通光:在垂直于光轴的方向上传播,折射率为 n o n_o no。
- extraordinary 光:在光轴方向上传播,折射率为 n e n_e ne,并且随着传播方向的变化,其折射率也会变化。
在光轴方向上,光的折射率 n e n_e ne 与传播方向的夹角 θ \theta θ 有关,可以通过下式描述:
n ( θ ) = n e 2 n o 2 n o 2 cos 2 θ + n e 2 sin 2 θ n(\theta) = \sqrt{ \frac{n_e^2 n_o^2}{n_o^2 \cos^2 \theta + n_e^2 \sin^2 \theta} } n(θ)=no2cos2θ+ne2sin2θne2no2
双曲介质(Hyperbolic Media)
-
对于折射率椭球,当 ϵ 3 > 0 \epsilon_3 > 0 ϵ3>0 时,其方程为:
k 1 2 + k 2 2 ϵ 3 + k 3 2 ϵ 1 = k o 2 ϵ o \frac{k_1^2 + k_2^2}{\epsilon_3} + \frac{k_3^2}{\epsilon_1} = \frac{k_o^2}{\epsilon_o} ϵ3k12+k22+ϵ1k32=ϵoko2
这表示一个旋转椭球,其长轴和短轴分别由 ϵ 3 \epsilon_3 ϵ3 和 ϵ 1 \epsilon_1 ϵ1 决定。 -
当 ϵ 3 < 0 \epsilon_3 < 0 ϵ3<0 时,方程变为:
k 1 2 + k 2 2 ϵ 3 − k 3 2 ϵ 1 = k o 2 ϵ o \frac{k_1^2 + k_2^2}{\epsilon_3} - \frac{k_3^2}{\epsilon_1} = \frac{k_o^2}{\epsilon_o} ϵ3k12+k22−ϵ1k32=ϵoko2
这表示一个旋转双曲面,其中 k 面显示为双曲线。
-
extraordinary k 面(extraordinary k Surface)
- 当 ϵ 3 \epsilon_3 ϵ3 为正时,extraordinary k 面是一个旋转椭球。
- 当 ϵ 3 \epsilon_3 ϵ3 为负时,extraordinary k 面是一个旋转双曲面。
-
折射率 n ( θ ) n(\theta) n(θ)
- 对于一个传播角度为 θ \theta θ 的 extraordinary 光,其折射率 n ( θ ) n(\theta) n(θ) 可以通过以下公式计算:
1 n 2 ( θ ) = cos 2 θ n o 2 − sin 2 θ n e 2 \frac{1}{n^2(\theta)} = \frac{\cos^2 \theta}{n_o^2} - \frac{\sin^2 \theta}{n_e^2} n2(θ)1=no2cos2θ−ne2sin2θ - 当 θ \theta θ 从 0 增加到 θ max = tan − 1 ( n e / n o ) \theta_{\text{max}} = \tan^{-1}(n_e / n_o) θmax=tan−1(ne/no) 时,折射率 n ( θ ) n(\theta) n(θ) 从 n o n_o no 增加到无穷大。
- 对于一个传播角度为 θ \theta θ 的 extraordinary 光,其折射率 n ( θ ) n(\theta) n(θ) 可以通过以下公式计算:
图示分析
-
旋转椭球(图(a))
- 该图表示当 ϵ 3 \epsilon_3 ϵ3 为正时的情况,k 面是一个旋转椭球。
- 红色箭头 k k k 表示波矢, s s s 表示光传播方向。
- θ \theta θ 是波矢与主轴的夹角。
-
旋转双曲面(图(b))
- 该图表示当 ϵ 3 \epsilon_3 ϵ3 为负时的情况,k 面是一个旋转双曲面。
- 此时,折射率 n ( θ ) n(\theta) n(θ) 随着 θ \theta θ 增加到 θ max \theta_{\text{max}} θmax 后达到无穷大。
折射率的变化
- 通过公式 1 n 2 ( θ ) = cos 2 θ n o 2 − sin 2 θ n e 2 \frac{1}{n^2(\theta)} = \frac{\cos^2 \theta}{n_o^2} - \frac{\sin^2 \theta}{n_e^2} n2(θ)1=no2cos2θ−ne2sin2θ,我们可以看到折射率 n ( θ ) n(\theta) n(θ) 是如何随着传播方向变化的。
- 当 θ \theta θ = 0 时, n ( θ ) = n o n(\theta) = n_o n(θ)=no,即折射率为普通光的折射率。
- 当 θ \theta θ 增加到 θ max = tan − 1 ( n e / n o ) \theta_{\text{max}} = \tan^{-1}(n_e / n_o) θmax=tan−1(ne/no) 时,折射率增加到无穷大。
近场成像系统通过利用双曲介质的独特特性,实现了亚波长分辨率的成像能力。这种系统的优势在于能够捕获高空间频率信息,并在各种高分辨率成像应用中表现出色。理解这些概念对于设计和应用先进的光学成像技术具有重要意义。
其他重要概念
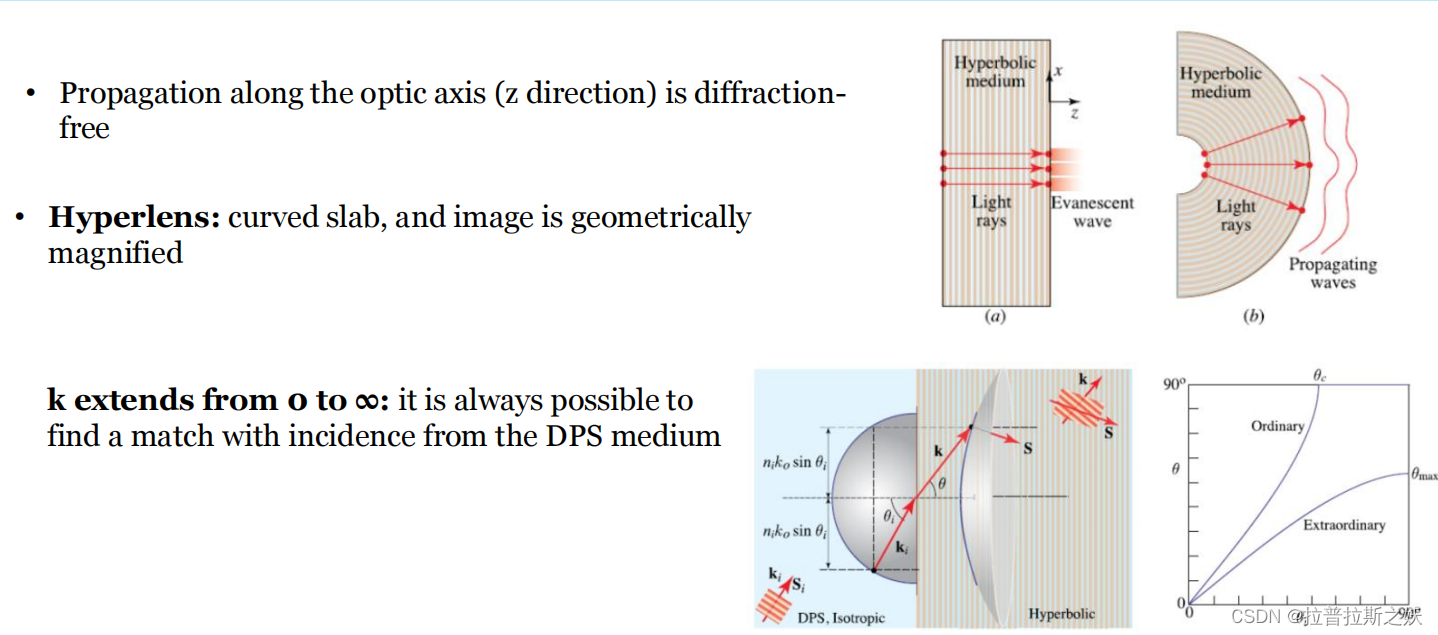
无衍射传播
在光学中,光波沿光轴(z方向)的传播通常会受到衍射的影响,导致光束扩散。然而,在特定的超材料(如双负材料或超介质)中,光可以实现无衍射传播。这意味着光波能够保持其原有的形状和方向,避免了在传播过程中因衍射引起的散射和扩展。
左上角的图示(图a)展示了光在超介质中的无衍射传播路径。光线在z方向上保持一致,没有散射或扩展。
超透镜(Hyperlens)
超透镜是一种利用超材料制成的特殊透镜,通常呈弯曲的薄板状。与传统透镜不同,超透镜能够实现几何放大成像。这种放大效果是通过操控光在超材料中的传播路径和速度来实现的。超透镜可以将亚波长尺度的信息放大到可见光范围,从而突破传统光学系统的衍射极限,获得更高的成像分辨率。
右上角的图示(图b)显示了超透镜如何通过弯曲的超介质板实现几何放大。光线经过超介质后,传播路径发生了改变,使得图像得以放大。
波矢k的扩展特性
在电磁波的传播理论中,波矢k描述了波的传播方向和波长。在DPS(Double Positive)介质中,波矢k的值可以从0扩展到无穷大,这意味着在这种介质中总能找到与入射波相匹配的传播模式。这种特性使得DPS介质能够有效地与其他介质(如SNG或DNG介质)耦合,从而实现复杂的光学功能。例如,在光纤通信中,利用这种耦合特性可以实现高效的信号传输和转换。
下方的图示描述了在不同介质(如DPS介质和各向同性介质)中的波矢k的分布情况。特别是右下角的图表展示了在超介质中的波矢k与入射波的匹配关系,表明无论入射角度如何,总能找到合适的传播模式。
