1 介绍
年份:2017
期刊: Advances in neural information processing systems
引用量:2829
Lopez-Paz D, Ranzato M A. Gradient episodic memory for continual learning[J]. Advances in neural information processing systems, 2017, 30.
本文提出的算法是Gradient Episodic Memory (GEM),它通过维护一个存储先前任务样本的情节记忆,并利用梯度信息来避免在持续学习过程中对先前任务性能的损害,同时允许对先前任务有益的知识传递。
2 创新点
- 新的评价指标:提出了一套新的度量标准来评估模型在连续数据流上的性能,不仅包括测试准确率,还包括模型在不同任务间的知识迁移能力。
- Gradient Episodic Memory (GEM)模型:提出了一种新的持续学习模型GEM,它通过情节记忆来减轻遗忘问题,同时允许对之前任务的知识进行有益的传递。
- 非独立同分布数据的处理:GEM模型能够处理非独立同分布的数据,即数据是按任务顺序观察到的,而不是从固定的概率分布中独立抽取的。
- 遗忘和迁移学习的优化:GEM通过优化策略在减少对先前任务性能的负面影响(即减轻遗忘)的同时,还试图实现对新任务的正向迁移。
- 梯度投影方法:GEM使用梯度投影方法来确保模型在更新参数时不会增加先前任务的损失,从而避免灾难性遗忘。
- 高效的计算:GEM的计算效率来自于它优化的是任务数量级别的变量,而不是模型参数数量级别的变量,这大大减少了计算量。
3 算法
3.1 算法原理
- 情节记忆(Episodic Memory):
- GEM算法维护一个情节记忆,该记忆存储了之前任务的样本。这些样本有助于在后续任务中避免遗忘先前学到的知识。
- 任务描述符(Task Descriptors):
- 算法使用任务描述符来识别每个样本所属的任务。这有助于模型区分和处理不同的任务。
- 非独立同分布数据(Non-iid Data):
- 算法设计来处理非独立同分布的数据,即数据是按任务顺序观察的,而不是随机抽取的。
- 梯度约束(Gradient Constraints):
- 在训练过程中,GEM使用梯度信息来确保新任务的学习不会增加先前任务的损失,从而避免灾难性遗忘。
- 梯度投影(Gradient Projection):
- GEM通过投影梯度到满足所有梯度约束的方向上来更新模型参数。这确保了对先前任务性能的保护。
- 正向和反向迁移(Forward and Backward Transfer):
- GEM旨在最小化对先前任务的负面影响(反向迁移),同时允许对新任务的正向迁移。
- 优化问题(Optimization Problem):
- GEM算法通过解决一个优化问题来更新模型参数,该问题包括最小化当前任务的损失,同时满足先前任务损失不增加的约束。
- 二次规划(Quadratic Programming):
- GEM算法使用二次规划来有效地解决梯度投影问题,这涉及到将原始问题转化为对任务数量(而不是参数数量)进行优化的对偶问题。
- 评估指标(Evaluation Metrics):
- 算法定义了一套评估指标,包括平均准确率(ACC)、反向迁移(BWT)和正向迁移(FWT),来衡量模型在连续学习任务中的表现。
3.4 算法步骤
- 初始化:
- 对于每个任务t,初始化一个空的情节记忆$ M_t $,用于存储该任务的部分样本。
- 观察数据:
- 模型按顺序观察数据,每个数据点由输入特征向量$ x_i 、任务描述符 、任务描述符 、任务描述符 t_i 和目标向量 和目标向量 和目标向量 y_i $组成。
- 更新情节记忆:
- 对于每个新观察到的样本,根据设定的存储策略(如存储最新的m个样本)更新对应任务的情节记忆。
- 计算当前任务的梯度:
- 对当前任务的样本计算梯度g,该梯度指向模型参数更新的方向。
- 计算先前任务的梯度:
- 对于所有先前任务k < t,计算在先前任务的样本在当前参数更新下的梯度$ g_k $ 。
- 梯度投影:
- 将当前梯度g投影到满足所有先前任务梯度约束的方向上,即找到一个更新方向$ \tilde{g} $,使得对所有先前任务的损失都不会增加。
- 梯度投影通过计算当前梯度与先前任务梯度之间的夹角,来确定参数更新方向,使得新任务的学习不会损害旧任务的性能。
- 将梯度投影问题转化为一个二次规划(Quadratic Programming, QP)问题。目标是最小化 g~ 与原始梯度 g 之间的欧几里得距离,同时满足它与所有先前任务的梯度 gkgk 之间的夹角满足一定条件(通常是非负条件),以保证先前任务的损失不会增加。
- $ min \hat{g} \frac{1}{2}∥\hat{g}−g∥^2_2 \
subject to⟨ \hat{g},g_k⟩≥ 0 $
- $ min \hat{g} \frac{1}{2}∥\hat{g}−g∥^2_2 \
- 二次规划问题可以通过多种数值方法求解,如内点法、梯度投影法或使用现有的QP求解器。在GEM算法中,作者提出了一种基于对偶问题的求解方法,通过求解对偶问题来找到原始问题的解。
- 参数更新:
- 使用投影后的梯度$ \tilde{g} $更新模型参数。
- 评估模型:
- 在每个任务学习完成后,使用测试集评估模型在所有任务上的性能,并记录评估结果。
- 计算评估指标:
- 根据评估结果计算平均准确率(ACC)、反向迁移(BWT)和正向迁移(FWT)。
- 迭代学习:
- 重复步骤2至9,直到所有任务的数据都被观察完毕。
- 返回模型和评估结果:
- 返回训练好的模型和评估矩阵( R ),其中包含了模型在连续学习过程中的性能指标。
5 实验分析
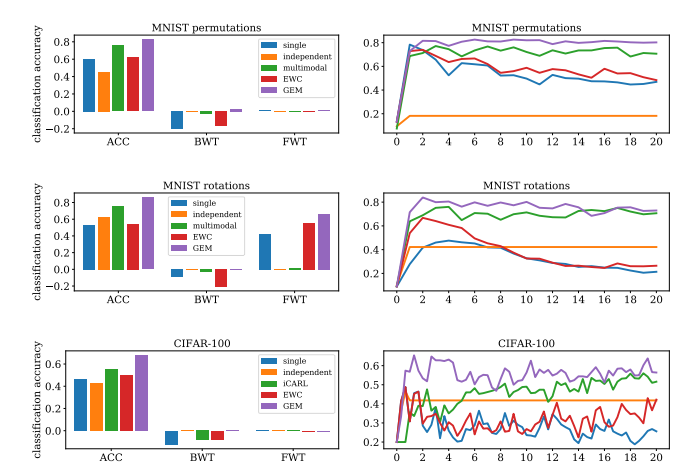
- 数据集:
- 使用了MNIST Permutations、MNIST Rotations和Incremental CIFAR100等变体数据集进行实验。
- 模型架构:
- 对于MNIST任务,使用了两层100个ReLU单元的全连接神经网络。
- 对于CIFAR100任务,使用了较小版本的ResNet18,并为每个任务添加了一个最终的线性分类器。
- 与现有技术的比较:
- 比较了GEM与五种其他方法:单一预测器、每个任务一个独立预测器、多峰值预测器、EWC(弹性权重合并)和iCARL。
- 性能指标:
- 考虑了平均准确率(ACC)、反向迁移(BWT)和正向迁移(FWT)作为性能指标。
- 实验结果:
- GEM在所有考虑的数据集上都显示出与多峰值模型相似或更好的性能,并且在反向迁移方面表现得更好,同时显示出轻微的或积极的正向迁移。
- 遗忘和迁移:
- GEM在CIFAR100数据集上展示了最小的遗忘,并在多个任务中对第一个任务的测试准确度表现出积极的反向迁移。
- 计算效率:
- GEM在计算上比其他持续学习方法(如EWC)更有效,并且在MNIST实验中的CPU训练时间更少。
- 记忆大小的影响:
- 在CIFAR100实验中,GEM的最终ACC随着情节记忆大小的增加而增加,表明GEM对记忆大小的调整更为鲁棒。
- 训练次数的影响:
- 在MNIST Rotations实验中,与没有记忆的方法相比,基于记忆的方法(如EWC和GEM)在数据上进行多次训练时表现出更高的ACC和更低的负面BWT。
- 与理想性能的比较:
- GEM在MNIST Rotations实验中的表现与通过所有任务的iid数据训练的单一预测器相当,达到了“理想性能上限”。
6 思考
(1)是先求当前任务样本的梯度?还是先求先前任务样本的梯度?
先求计算当前任务样本的梯度,再计算先前任务样本的梯度
(2)本文中计算先前任务的梯度,是根据当前先前任务样本在当前模型上的计算得到。而不是训练之前任务存储的。
