训练深层神经网络是十分困难的,光是之前简单的模型在简单的数据集上训练都不太轻松。
而批量规范化(batch normalization)是一种流行且有效的技术,可以帮助加快深层网络的收敛速度。
一、训练深层网络
我们回顾一下训练神经网络时出现的一些挑战。
首先,数据预处理的方式通常对最终结果产生巨大影响。
第二,对于典型的多层感知机或卷积神经网络,当我们训练时,中间层的变量可能具有更广的变化范围,随着训练更新的模型参数变幻莫测。
第三,更深层的网络很复杂,容易过拟合。
批量规范化应用于单个可选层(也可应用到所有层),其原理如下:
在每次迭代训练中,我们首先规范化输入,即通过减去其均值并除以其标准差,其中两者均基于当前小批量得到。接下来,我们应用比例系数和比例偏移。
需要注意的是,如果批量大小为 1,减去均值之后,每个隐藏单元将变为 0,那我们将无法学习到任何东西。
因此,只有使用足够大的小批量,批量规范化这种方法才是有效且稳定的。所以在应用批量规范化时,批量大小的选择相当重要。
二、批量规范化层
和激活函数、丢弃法(dropout)一样,批量规范化可看成一层网络:批量规范化层。
对于全连接层和卷积层,它们的批量规范化实现略有不同。
全连接层的批量规范化作用在特征维度上,而卷积层作用在通道维度上。
把图像的像素视为样本,通道视为特征,卷积层可理解为高维的全连接层。
全连接层
通常,我们将批量规范化层置于全连接层中的仿射变换和激活函数之间。
设全连接层的输入为 x x x,权重参数和偏置参数分别为 W \pmb{W} W 和 b \pmb{b} b,激活函数为 ϕ \phi ϕ,批量规范化的运算符为 BN。
那么,使用批量规范化的全连接层的输出 h \pmb{h} h计算详情为:
h = ϕ ( B N ( W x + b ) ) . \pmb{h}=\phi(BN(\pmb{W}\pmb{x}+\pmb{b})). h=ϕ(BN(Wx+b)).
卷积层
同样,对于卷积层,我们可以在卷积层之后和非线性激活函数之前应用批量规范化。
当卷积层有多个输出通道时,我们需要对这些通道的“每个”输出执行批量规范化,每个通道都有自己的拉伸(scale)和偏移(shift)参数。
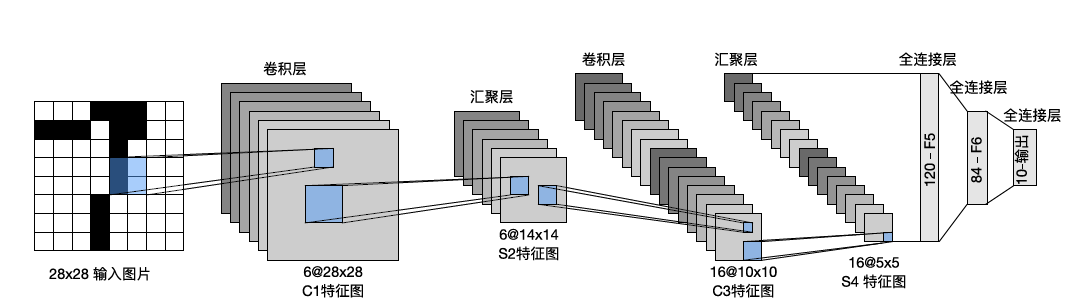
三、使用批量规范化层的 LeNet
回顾一下 LeNet 架构,一层 5$\times 5 卷积,填充大小为 2 ,输出通道数为 6 ;一层 2 5 卷积,填充大小为 2,输出通道数为 6;一层 2 5卷积,填充大小为2,输出通道数为6;一层2\times 2 汇聚层,步幅为 2 ;再一层 5 2 汇聚层,步幅为 2;再一层 5 2汇聚层,步幅为2;再一层5\times 5 卷积层,输出通道数为 16 ;之后一层 2 5 卷积层,输出通道数为 16;之后一层 2 5卷积层,输出通道数为16;之后一层2\times$2 汇聚层,步幅为 2;最后展平加上三层全连接层。
代码实现为:
net = nn.Sequential( # LeNet模型nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Flatten(),nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),nn.Linear(120, 84), nn.Sigmoid(),nn.Linear(84, 10))
若想添加批量规范化层,在相应位置处加入相应的nn.BatchNorm即可。全连接层使用nn.BatchNorm1d,即 1 维;卷积层使用nn.BatchNorm2d,即 2 维。
传入的参数为全连接层的输出数量或卷积层的输出通道数,代码实现为:
net = nn.Sequential( # 带BN的LeNet模型nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.BatchNorm2d(6), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Flatten(),nn.Linear(16 * 5 * 5, 120), nn.BatchNorm1d(120), nn.Sigmoid(),nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),nn.Linear(84, 10))
由于批量规范化的作用是加快收敛速度,因此需要关注这 10 轮训练的损失变化情况,我们利用 tensorboard 来可视化。
运行后得到的损失变化图如下:
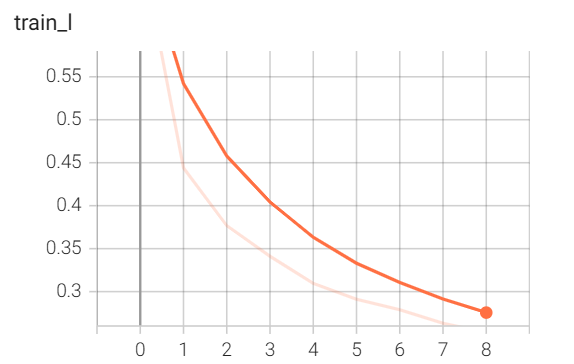
我们再运行之前写的 LeNet 模型,其损失变化图为:
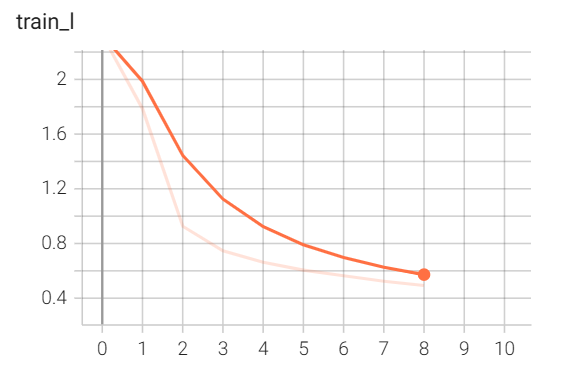
可以发现加了 BN 后,训练损失收敛加快了不少(纵轴的范围),早早地就降低为 0.55;而最初的 LeNet,训练了好多轮后才到达同样的损失水平。
总结一下:
- 在模型训练过程中,批量规范化利用小批量的均值和标准差,不断调整神经网络的中间输出,使得整个神经网络各层的中间输出值更加稳定,从而加快收敛速度。
- 批量规范化在全连接层和卷积层的使用均略有不同。
上次 VGG 的代码和这次批量规范化的代码见附件:
