LeetCode 每周算法 6(图论、回溯)
图论算法:

class Solution: def dfs(self, grid: List[List[str]], r: int, c: int) -> None: """ 深度优先搜索函数,用于遍历并标记与当前位置(r, c)相连的所有陆地(即值为"1"的格子)为已访问(即标记为0)。 :param grid: 二维网格,其中的每个元素都是'0'或'1'。 :param r: 当前遍历到的行索引。 :param c: 当前遍历到的列索引。 """ grid[r][c] = '0' nr, nc = len(grid), len(grid[0]) for x, y in [(r - 1, c), (r + 1, c), (r, c - 1), (r, c + 1)]: if 0 <= x < nr and 0 <= y < nc and grid[x][y] == "1": self.dfs(grid, x, y) def numIslands(self, grid: List[List[str]]) -> int: """ 计算给定网格中的岛屿数量。 :param grid: 二维网格,其中的每个元素都是'0'或'1'。 :return: 网格中的岛屿数量。 """ nr = len(grid) if nr == 0: return 0 nc = len(grid[0]) num_islands = 0 for r in range(nr): for c in range(nc): if grid[r][c] == "1": num_islands += 1 self.dfs(grid, r, c) return num_islands

class Solution: def orangesRotting(self, grid: List[List[int]]) -> int: R, C = len(grid), len(grid[0]) queue = deque() for r, row in enumerate(grid): for c, val in enumerate(row): if val == 2: queue.append((r, c, 0)) def neighbors(r, c): for nr, nc in ((r - 1, c), (r, c - 1), (r + 1, c), (r, c + 1)): if 0 <= nr < R and 0 <= nc < C: yield nr, nc d = 0 while queue: r, c, d = queue.popleft() for nr, nc in neighbors(r, c): if grid[nr][nc] == 1: grid[nr][nc] = 2 queue.append((nr, nc, d + 1)) if any(1 in row for row in grid): return -1 return d

class Solution: def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool: edges = collections.defaultdict(list) indeg = [0] * numCourses for info in prerequisites: edges[info[1]].append(info[0]) indeg[info[0]] += 1 q = collections.deque([u for u in range(numCourses) if indeg[u] == 0]) visited = 0 while q: visited += 1 u = q.popleft() for v in edges[u]: indeg[v] -= 1 if indeg[v] == 0: q.append(v) return visited == numCourses

class Trie: def __init__(self): self.children = [None] * 26 self.isEnd = False def searchPrefix(self, prefix: str) -> "Trie": node = self for ch in prefix: ch = ord(ch) - ord("a") if not node.children[ch]: return None node = node.children[ch] return node def insert(self, word: str) -> None: node = self for ch in word: ch = ord(ch) - ord("a") if not node.children[ch]: node.children[ch] = Trie() node = node.children[ch] node.isEnd = True def search(self, word: str) -> bool: node = self.searchPrefix(word) return node is not None and node.isEnd def startsWith(self, prefix: str) -> bool: return self.searchPrefix(prefix) is not None
图论算法:

class Solution {
public: void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len) { if (first == len) { res.emplace_back(output); return; } for (int i = first; i < len; ++i) { swap(output[i], output[first]); backtrack(res, output, first + 1, len); swap(output[i], output[first]); } } vector<vector<int>> permute(vector<int>& nums) { vector<vector<int>> res; backtrack(res, nums, 0, (int)nums.size());return res; }
};

class Solution {
public: vector<int> output; vector<vector<int>> ans; vector<vector<int>> subsets(vector<int>& nums) { for (int mask = 0; mask < (1 << nums.size()); ++mask) { output.clear(); for (int i = 0; i < nums.size(); ++i) { if (mask & (1 << i)) { output.push_back(nums[i]); } } ans.push_back(output); } return ans; }
};

class Solution {
public: vector<string> letterCombinations(string digits) { if (digits.empty()) { return combinations; } string combination; vector<string> combinations; unordered_map<char, string> phoneMap{ {'2', "abc"}, {'3', "def"}, {'4', "ghi"}, {'5', "jkl"}, {'6', "mno"}, {'7', "pqrs"}, {'8', "tuv"}, {'9', "wxyz"} }; backtrack(combinations, phoneMap, digits, 0, combination); return combinations; } void backtrack(vector<string>& combinations, const unordered_map<char, string>& phoneMap, const string& digits, int index, string& combination) { if (index == digits.length()) { combinations.push_back(combination); } else { char digit = digits[index]; const string& letters = phoneMap.at(digit); for (const char& letter: letters) { combination.push_back(letter); backtrack(combinations, phoneMap, digits, index + 1, combination); combination.pop_back(); } } }
};

class Solution {
public: vector<vector<int>> result; vector<int> path; void backtrack(const vector<int>& candidates, int target, int start) { if (target < 0) return; if (target == 0) { result.push_back(path); return; } for (int i = start; i < candidates.size() && target - candidates[i] >= 0; i++) { path.push_back(candidates[i]); backtrack(candidates, target - candidates[i], i); path.pop_back(); } } vector<vector<int>> combinationSum(vector<int>& candidates, int target) { sort(candidates.begin(), candidates.end()); backtrack(candidates, target, 0); return result; }
};

class Solution { void backtrack(vector<string>& result, string& current, int left, int right, int n) { if (current.size() == n * 2) { result.push_back(current); return; } if (left < n) { current.push_back('('); backtrack(result, current, left + 1, right, n); current.pop_back(); } if (right < left) { current.push_back(')'); backtrack(result, current, left, right + 1, n); current.pop_back(); } } public: vector<string> generateParenthesis(int n) { vector<string> result; string current; backtrack(result, current, 0, 0, n); return result; }
};

class Solution {
public: bool exist(vector<vector<char>>& board, string word) { for (int i = 0; i < board.size(); i++) { for (int j = 0; j < board[0].size(); j++) { vector<vector<bool>> visited(board.size(), vector<bool>(board[0].size(), false)); if (dfs(board, visited, word, 0, i, j)) return true; } } return false; } private: bool dfs(vector<vector<char>>& board, vector<vector<bool>>& visited, const string& word, int str_index, int i, int j) { if (str_index == word.size()) return true; if (i >= board.size() || i < 0 || j >= board[0].size() || j < 0 || visited[i][j] == true || board[i][j] != word[str_index]) return false; visited[i][j] = true; if (dfs(board, visited, word, str_index + 1, i + 1, j) || dfs(board, visited, word, str_index + 1, i - 1, j) || dfs(board, visited, word, str_index + 1, i, j + 1) || dfs(board, visited, word, str_index + 1, i, j - 1)) return true; visited[i][j] = false; return false; }
};

class Solution {
private: vector<vector<int>> dp; vector<vector<string>> result; vector<string> answer; int n; public: void dfs(const string& s, int i) { if (i == n) { result.push_back(answer); return; } for (int j = i; j < n; ++j) { if (dp[i][j]) { answer.push_back(s.substr(i, j - i + 1)); dfs(s, j + 1); answer.pop_back(); } } } vector<vector<string>> partition(string s) { n = s.size(); dp.assign(n, vector<int>(n, true)); for (int i = n - 1; i >= 0; --i) { for (int j = i; j < n; ++j) { dp[i][j] = (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])); } } dfs(s, 0); return result; }
};
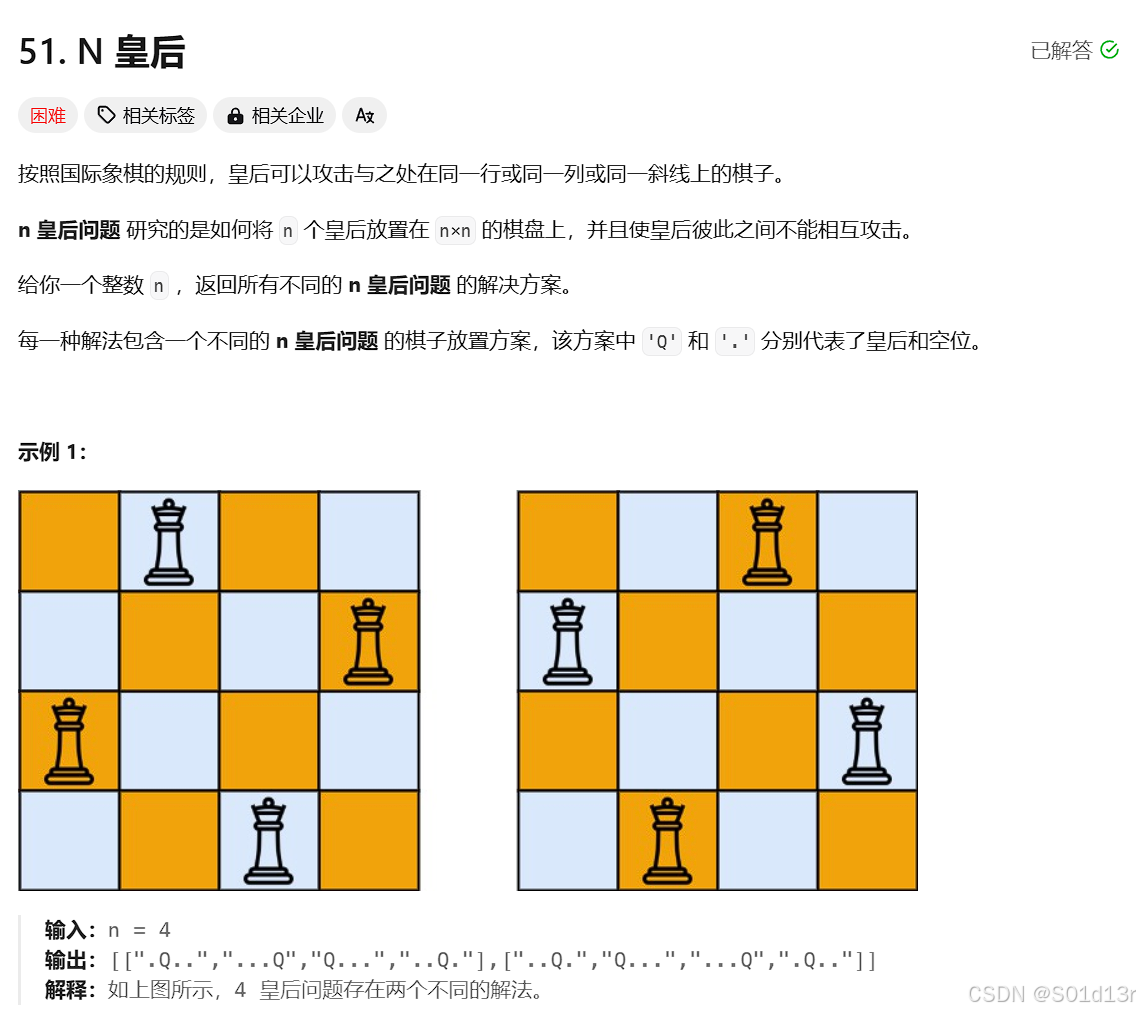
class Solution {
private: vector<vector<string>> result; void backtracking(int n, int row, vector<string>& chessboard) { if (row == n) { result.push_back(chessboard); return; } for (int col = 0; col < n; col++) { if (isvalid(row, col, chessboard, n)) { chessboard[row][col] = 'Q'; backtracking(n, row + 1, chessboard); chessboard[row][col] = '.'; } } } bool isvalid(int row, int col, vector<string>& chessboard, int n) { for (int i = 0; i < row; i++) { if (chessboard[i][col] == 'Q') { return false; } } for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) { if (chessboard[i][j] == 'Q') { return false; } } for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) { if (chessboard[i][j] == 'Q') { return false; } } return true; } public: vector<vector<string>> solveNQueens(int n) { result.clear(); vector<string> chessboard(n, string(n, '.')); backtracking(n, 0, chessboard); return result; }
};












