一、131.分割回文串
131. 分割回文串 - 力扣(LeetCode)
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]
思路:
我们来分析一下切割,其实切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
感受出来了不?
所以切割问题,也可以抽象为一棵树形结构,如图:
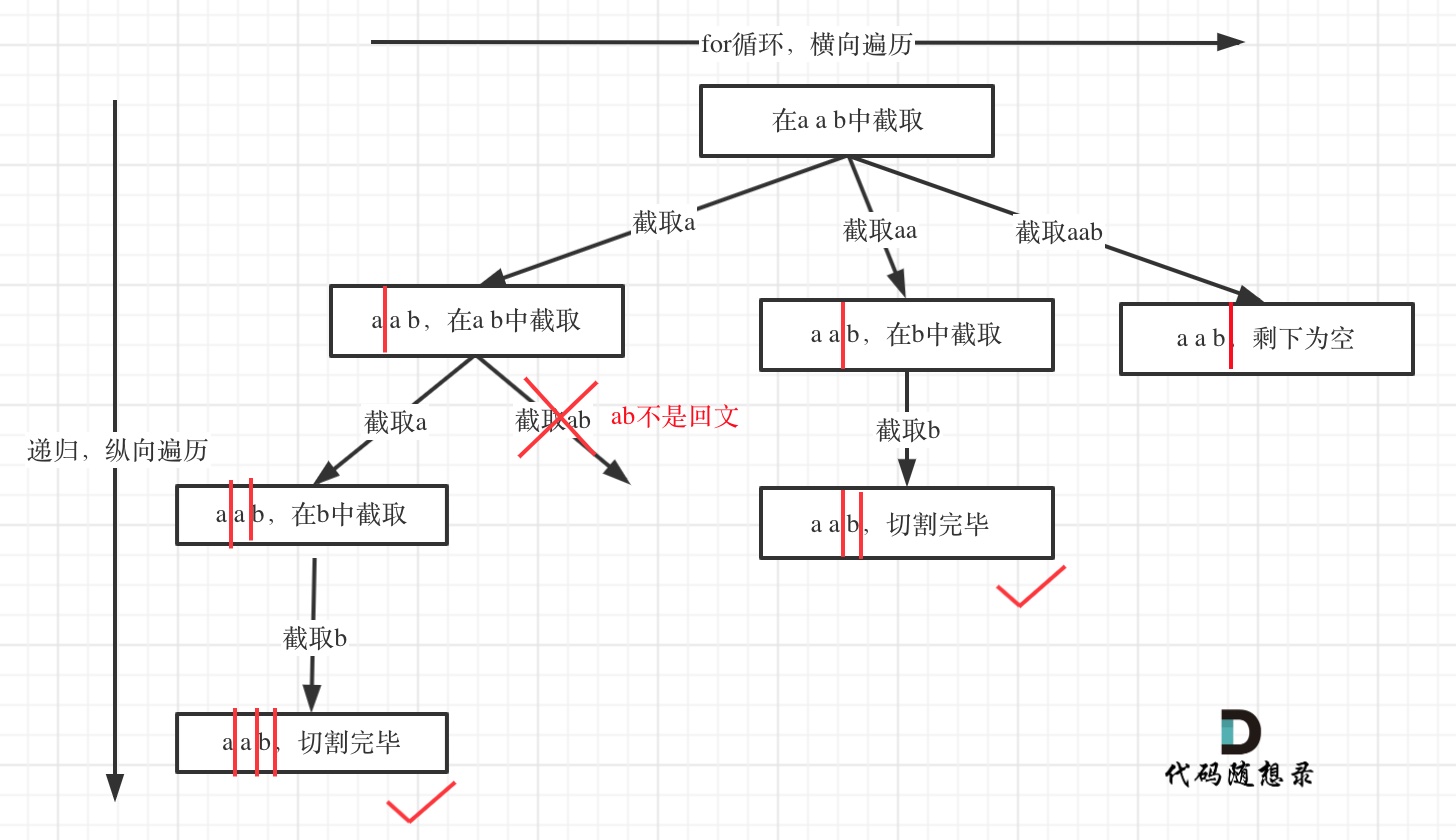
递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
此时可以发现,切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。
- 递归函数参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。 (这两个参数可以放到函数参数里)
本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
- 递归函数终止条件

从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
那么在代码里什么是切割线呢?
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
- 单层搜索的逻辑
来看看在递归循环中如何截取子串呢?
在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
判断回文子串
可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
class Solution:def partition(self, s: str) -> List[List[str]]:'''递归用于纵向遍历for循环用于横向遍历当切割线迭代至字符串末尾,说明找到一种方法类似组合问题,为了不重复切割同一位置,需要start_index来做标记下一轮递归的起始位置(切割线)'''result = []self.backtracking(s, 0, [], result)return resultdef backtracking(self, s, start_index, path, result ):# Base Caseif start_index == len(s):result.append(path[:])return# 单层递归逻辑for i in range(start_index, len(s)):# 此次比其他组合题目多了一步判断:# 判断被截取的这一段子串([start_index, i])是否为回文串if self.is_palindrome(s, start_index, i):path.append(s[start_index:i+1])self.backtracking(s, i+1, path, result) # 递归纵向遍历:从下一处进行切割,判断其余是否仍为回文串path.pop() # 回溯def is_palindrome(self, s: str, start: int, end: int) -> bool:i: int = start j: int = endwhile i < j:if s[i] != s[j]:return Falsei += 1j -= 1return True 二、93.复原IP地址
93. 复原 IP 地址 - 力扣(LeetCode)
思路:
判断子串是否合法
最后就是在写一个判断段位是否是有效段位了。
主要考虑到如下三点:
- 段位以0为开头的数字不合法
- 段位里有非正整数字符不合法
- 段位如果大于255了不合法
-
def is_valid(self, s, start, end):if start > end:return Falseif s[start] == '0' and start != end: # 0开头的数字不合法return Falsenum = 0for i in range(start, end + 1):if not s[i].isdigit(): # 遇到非数字字符不合法return Falsenum = num * 10 + int(s[i])if num > 255: # 如果大于255了不合法return Falsereturn True
完整代码
class Solution:def restoreIpAddresses(self, s: str) -> List[str]:result = []self.backtracking(s, 0, 0, "", result)return resultdef backtracking(self, s, start_index, point_num, current, result):if point_num == 3: # 逗点数量为3时,分隔结束if self.is_valid(s, start_index, len(s) - 1): # 判断第四段子字符串是否合法current += s[start_index:] # 添加最后一段子字符串result.append(current)returnfor i in range(start_index, len(s)):if self.is_valid(s, start_index, i): # 判断 [start_index, i] 这个区间的子串是否合法sub = s[start_index:i + 1]self.backtracking(s, i + 1, point_num + 1, current + sub + '.', result)else:breakdef is_valid(self, s, start, end):if start > end:return Falseif s[start] == '0' and start != end: # 0开头的数字不合法return Falsenum = 0for i in range(start, end + 1):if not s[i].isdigit(): # 遇到非数字字符不合法return Falsenum = num * 10 + int(s[i])if num > 255: # 如果大于255了不合法return Falsereturn True三、78.子集
78. 子集 - 力扣(LeetCode)
思路:
class Solution:def subsets(self, nums):result = []path = []self.backtracking(nums, 0, path, result)return resultdef backtracking(self, nums, startIndex, path, result):result.append(path[:]) # 收集子集,要放在终止添加的上面,否则会漏掉自己# if startIndex >= len(nums): # 终止条件可以不加# returnfor i in range(startIndex, len(nums)):path.append(nums[i])self.backtracking(nums, i + 1, path, result)path.pop()