安阳哪个公司做网站好_原创服装设计师_seo培训一对一_企业培训考试

1.线性回归简介

线性回归知识讲解

定义与公式
- 定义：线性回归是利用回归方程（函数）对自变量（特征值）和因变量（目标值）之间关系进行建模的分析方式。自变量只有一个时是单变量回归，超过一个就是多元回归。
- 公式：
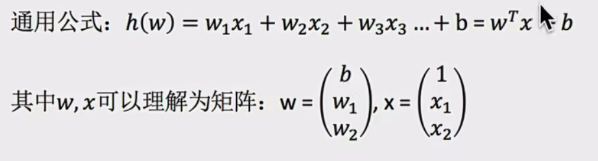
特征与目标的关系分析 线性回归模型分线性关系和非线性关系。单变量线性关系中，像房子面积和房子价格，从图中散点分布能看出大致呈直线趋势，说明两者存在线性相关关系，可通过线性回归方程拟合这条直线来描述它们之间的数量关系，进而预测房价等。非线性关系则不呈现这种直线特征，其关系更复杂。比如：

再比如非线性关系：

2.回归的损失和优化：

损失函数
- 定义：总损失，其中yi是第i个训练样本真实值，h（xi）是第i个训练样本特征值组合预测函数。它衡量了预测值与真实值之间的误差，通过最小化这个损失函数，能让模型预测更准确，也被称为最小二乘法。（其实还有其他定义这个误差的办法）
优化算法
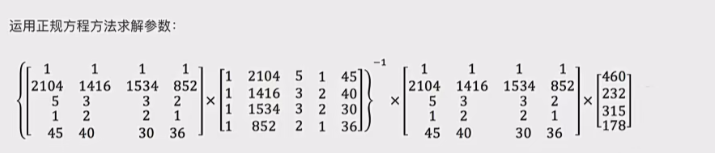
- 正规方程
  - 公式：，X为特征值矩阵（就是我们的数据，不包括标签值），y为目标值矩阵。可直接求解得到使损失最小的参数w。
  - 缺点：当特征过多过复杂时，计算逆矩阵求解速度慢，甚至可能无法得到结果。所以正规方程适合小规模数据，梯度下降适合大规模数据
  - 正规方程的推导：其实第一行最后一项是xw-y（n*1）矩阵每行平方求和，简写为那样
  - 案例：
- 梯度下降
  - 基本思想：类比下山过程，以当前位置为基准，寻找最陡峭方向（即梯度方向），朝着梯度相反方向走（因为梯度方向是函数上升最快方向，其反方向是下降最快方向），重复此过程找到函数最小值。其实就是我们运筹学中讲过的优化办法的框架中方向的特定情况（牛顿法）：1.确定初始位置 2.确定方向t 3.确定步长a 4.确定终止条件，迭代公式为当前位置=过去位置+at，梯度下降就是方向是梯度。
  - 梯度概念：单变量函数中，梯度是函数微分，代表给定点切线斜率；多变量函数中，梯度是向量，其方向是函数上升最快方向。
  - 公式：。其中a是学习率（步长），控制每次更新的幅度，a太大会错过最低点，太小则收敛缓慢；梯度前乘负号，是为了朝着梯度相反方向（即函数下降最快方向）更新参数。
  - 案例：

3.梯度下降法详解

3.1推导流程：

3.2分类

梯度下降法家族算法总结6

全梯度下降算法（FG）
- 原理：计算训练集所有样本误差并求平均作为目标函数，利用所有样本计算损失函数关于参数theta的梯度，权重向量沿梯度反方向移动。公式为：
- 优缺点：优点是能准确朝着最优解方向更新；缺点是计算所有样本梯度，速度慢，无法处理超内存数据集，不能在线更新模型。
随机梯度下降算法（SG）
- 原理：每次只代入计算一个样本目标函数的梯度来更新权重，不断重复，直至损失函数值满足停止条件。迭代公式为（无求和了）：
- 优缺点：优点是简单高效，可避免收敛到局部最优解；缺点是仅用单个样本迭代，遇噪声易陷入局部最优解。
小批量梯度下降算法（mini - batch）（结合FG和SG,随机拿出部分样本全部用于计算）
- 原理：从训练样本集随机抽取小样本集（batch_size 个样本），在小样本集上采用全梯度下降迭代更新权重。迭代公式为：（从i到i+x-1求和说明就是选取了x个样本）
- 特点：是 FG 和 SG 的折中方案，batch_size 常设为 2 的幂次方利于 GPU 加速，batch_size = 1 时为 SG，batch_size = n（样本总数）时为 FG 。
随机平均梯度下降算法（SAG）
- 原理：内存中维护每个样本旧梯度，随机选样本更新其梯度，其他样本梯度不变，求所有梯度平均值更新参数。迭代公式为
- 优缺点：计算成本与 SG 相当，但收敛速度快得多，兼具随机性与确定性，计算成本低于 mini - batch sgd 。

4.API介绍（和其他一样，先会生成一个对象，然后再用对象的方法）以及回归评估

4.1 API介绍偏置就是那个回归方程中的常数，SGD函数里边的正则化和loss函数以后会讲，这里采用的loss是我们讲的最小二乘法。

SGDRegressor（max_iter=1000）表示最多迭代1000次

4.2回归误差如何衡量：

MSE是最小二乘法的目标函数！！！

4.3 案例：

正归法案例：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_errordef linear_model1():"""线性回归:正规方程:return:None"""# 1.获取数据data = load_boston()# 2.数据集划分x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)# 3.特征工程-标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.fit_transform(x_test)# 4.机器学习-线性回归(正规方程)estimator = LinearRegression()estimator.fit(x_train, y_train)# 5.模型评估# 5.1 获取系数等值y_predict = estimator.predict(x_test)print("预测值为:\n", y_predict)print("模型中的系数为:\n", estimator.coef_)print("模型中的偏置为:\n", estimator.intercept_)# 5.2 评价# 均方误差error = mean_squared_error(y_test, y_predict)print("误差为:\n", error)return None

梯度下降法案例：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_errordef linear_model2():"""线性回归:梯度下降法:return:None"""# 1.获取数据data = load_boston()# 2.数据集划分x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)# 3.特征工程-标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.fit_transform(x_test)# 4.机器学习-线性回归(梯度下降)estimator = SGDRegressor(max_iter=1000)estimator.fit(x_train, y_train)# 5.模型评估# 5.1 获取系数等值y_predict = estimator.predict(x_test)print("预测值为:\n", y_predict)print("模型中的系数为:\n", estimator.coef_)print("模型中的偏置为:\n", estimator.intercept_)# 5.2 评价# 均方误差error = mean_squared_error(y_test, y_predict)print("误差为:\n", error)return None

6.欠拟合和过拟合

定义
- 过拟合：模型在训练集上拟合效果好，但在测试集上表现差，原因是模型过于复杂，捕捉到了训练数据中的噪声和特殊细节。
- 欠拟合：模型在训练集和测试集上拟合效果都不好，是因为模型过于简单，无法学习到数据中的规律。
原因及解决办法
- 欠拟合
  - 原因：学习到的数据特征过少。
  - 解决办法：添加其他特征项，如 “组合”“泛化”“相关性” 特征，以及上下文、平台特征等；添加多项式特征，提升模型泛化能力。
- 过拟合
  - 原因：原始特征过多，存在嘈杂特征，模型为兼顾各测试数据点变得复杂。
  - 解决办法：重新清洗数据；增大训练量；采用正则化；减少特征维度。
正则化（过拟合的处理）
- 概念：在训练过程中，让算法尽量减少某些影响模型复杂度或异常数据多的特征的作用，通过调整参数优化结果，而非直接识别特定特征影响。
- 类别
  - L2 正则化：使部分权重W趋近于 0 ，削弱特征影响，对应 Ridge （岭）回归。
  - L1 正则化：使部分权重W直接为 0 ，删除特征影响，对应 LASSO 回归。

7.正则化详解（这些回归都是不同类型的损失函数，前面讲的梯度下降法是求解最优值的办法。）

一些补充：

关于l1正则化lasso回归的导数：

知道api即可，着重讲岭回归，因为经常用。。很少用普通的回归。

正则就相当于惩罚力度，越大则权重越小，就能处理过拟合。

8.岭回归详解

这个api函数可以自己进行标准化。

案例：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_errordef linear_model3():"""线性回归:岭回归:return:"""# 1.获取数据data = load_boston()# 2.数据集划分x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)# 3.特征工程-标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.fit_transform(x_test)# 4.机器学习-线性回归(岭回归)estimator = Ridge(alpha=1)estimator.fit(x_train, y_train)# 5.模型评估# 5.1 获取系数等值y_predict = estimator.predict(x_test)print("预测值为:\n", y_predict)print("模型中的系数为:\n", estimator.coef_)print("模型中的偏置为:\n", estimator.intercept_)# 5.2 评价# 均方误差error = mean_squared_error(y_test, y_predict)print("误差为:\n", error)return Noneif __name__ == '__main__':linear_model3()

9.模型的加载和保存

很简单就是调用函数就行。后面是路径

还是上面的案例：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
import joblibdef load_dump_demo():"""模型保存和加载:return:"""# 1.获取数据data = load_boston()# 2.数据集划分x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)# 3.特征工程-标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.fit_transform(x_test)# 4.机器学习-线性回归(岭回归)# 4.1 模型训练estimator = Ridge(alpha=1)estimator.fit(x_train, y_train)# 4.2 模型保存joblib.dump(estimator, "./data/test.pkl")# 4.3 模型加载estimator = joblib.load("./data/test.pkl")# 5.模型评估# 5.1 获取系数等值y_predict = estimator.predict(x_test)print("预测值为:\n", y_predict)print("模型中的系数为:\n", estimator.coef_)print("模型中的偏置为:\n", estimator.intercept_)# 5.2 评价# 均方误差error = mean_squared_error(y_test, y_predict)print("误差为:\n", error)return Noneif __name__ == '__main__':load_dump_demo()

安阳哪个公司做网站好_原创服装设计师_seo培训一对一_企业培训考试

线性回归知识讲解

梯度下降法家族算法总结6

最新新闻

热搜词