深度优先搜索(DFS)就是一种寻找图中各个顶点的方法。想象一下,如果你在一个迷宫里探险,你会怎么做呢?你可能会选择一直走到尽头,直到找不到路为止,然后再回过头来试试其他的路,这就是深度优先搜索的基本思路!让我们来看看 DFS 是如何工作的。假设你在一个图中,想要找到所有的顶点。我们可以从一个顶点开始,沿着一条边走下去,直到没有新的顶点可以访问为止。然后我们再回到上一个顶点,尝试另一条边。这种方法就像爬树一样:你会先爬到树的最高处,然后再慢慢往下走,看看其他的分支。
举个例子 让我们通过一个简单的例子来说明 DFS。假设我们有这样一个图: ``` A / \ B C | | D E ``` 在这个图中,A、B、C、D、E 都是顶点,而连线就是边。我们从顶点 A 开始进行 DFS: 1. **从 A 开始**:我们访问 A。 2. **访问 B**:从 A 出发,我们可以选择去 B。我们现在在 B。 3. **访问 D**:从 B,我们可以选择去 D。现在我们在 D。 4. **回退到 B**:D 没有其他未访问的顶点,所以我们回到 B。 5. **回退到 A**:然后,我们从 B 回到 A。 6. **访问 C**:接下来,我们去 C。 7. **访问 E**:从 C,我们去 E。 最终的访问顺序是:A → B → D → C → E。这就是深度优先搜索的过程!
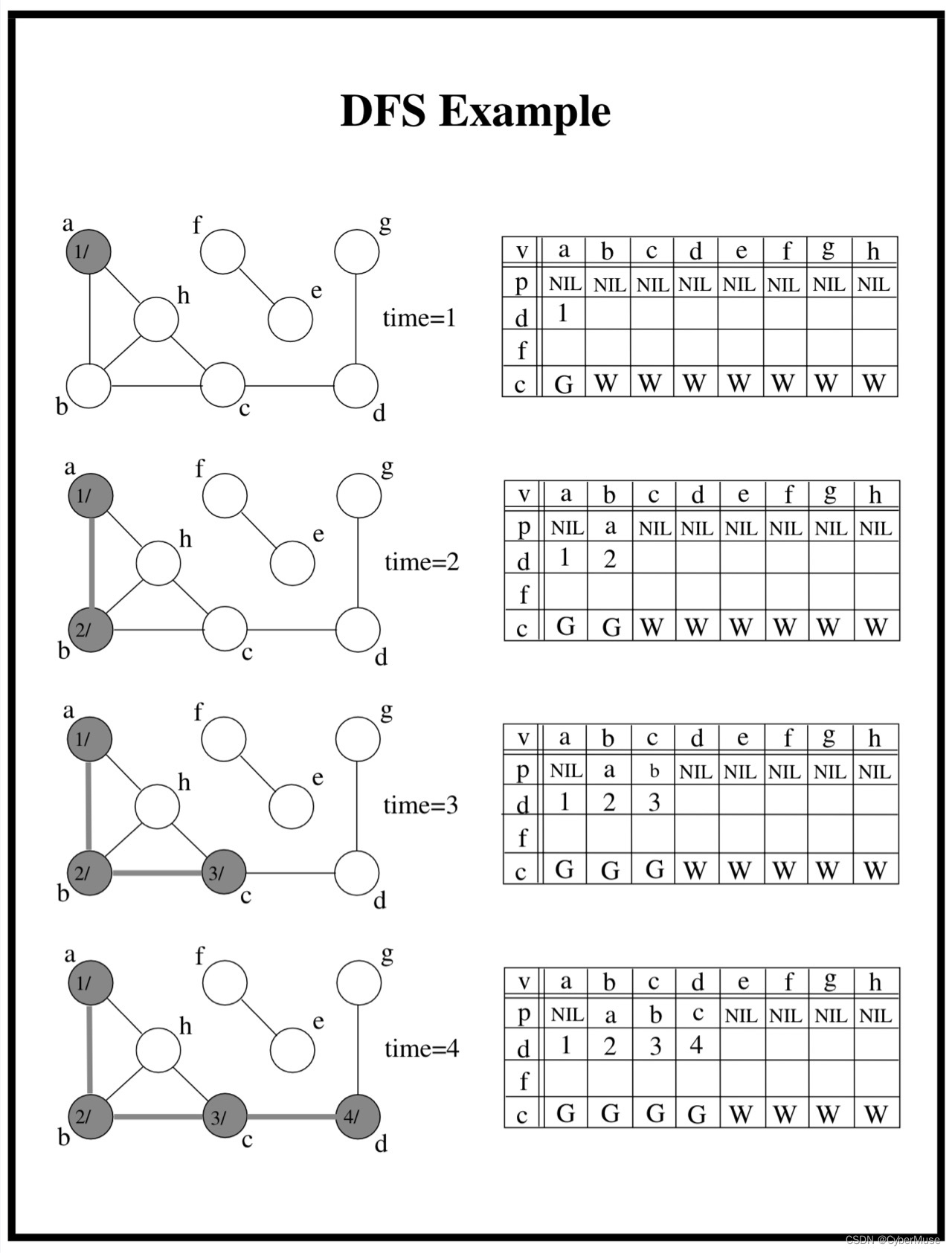
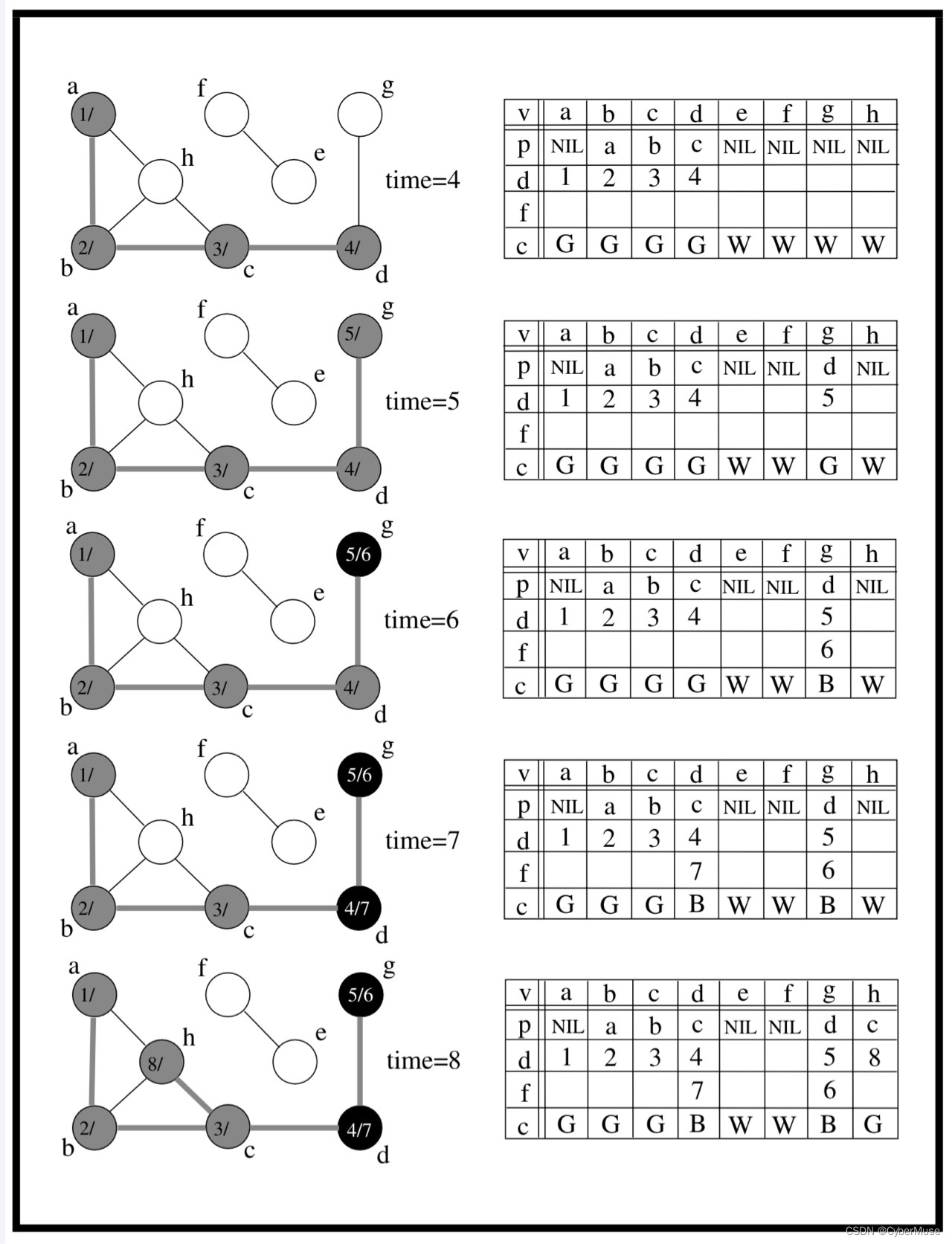
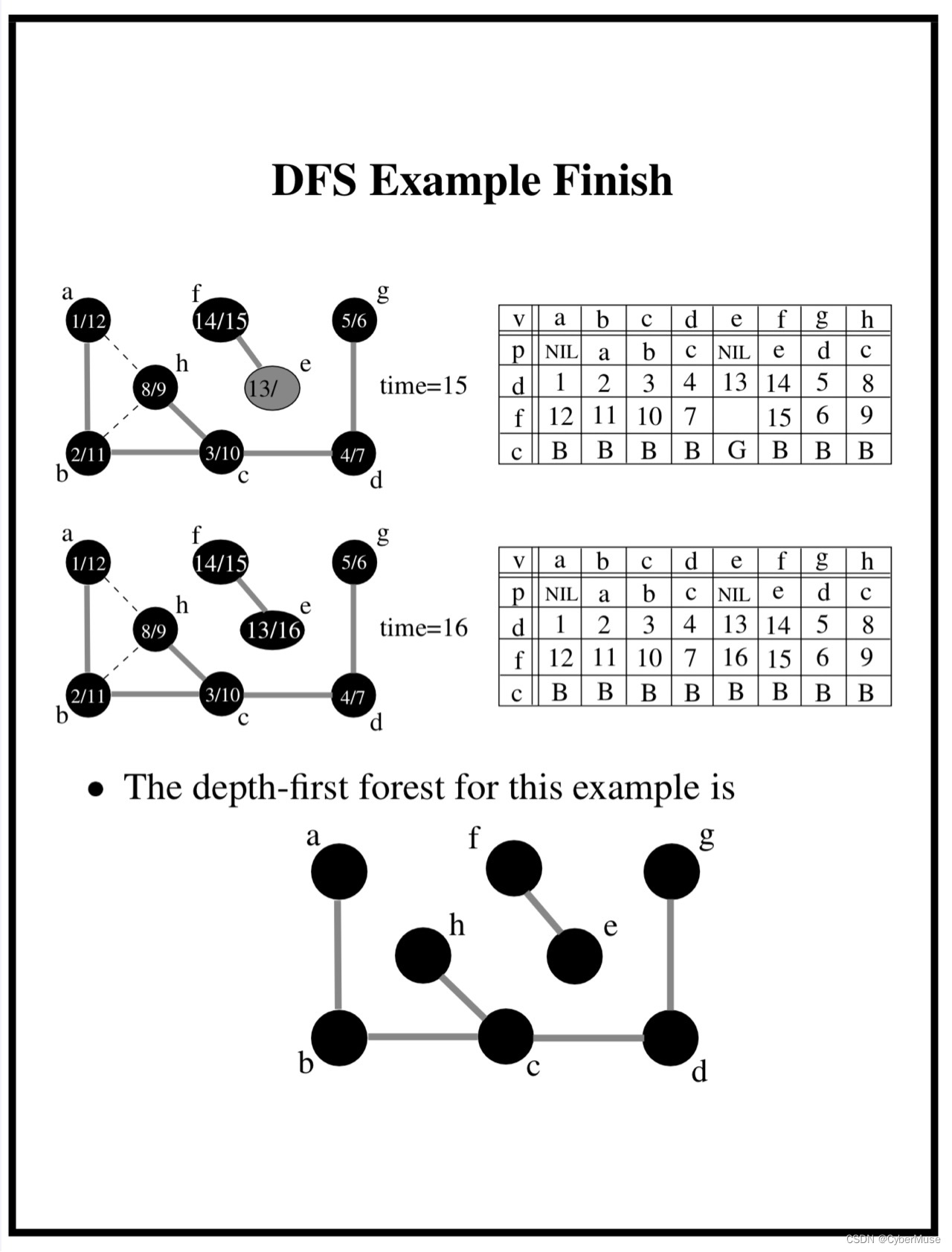
时间戳 :在 DFS 中,我们还会记录每个顶点的访问时间。比如说,当我们第一次访问 A 时,我们可以记录一个时间点(比如说,1),当我们完成访问 A 的所有邻接顶点后,我们再记录另一个时间点(比如说,6)。这样,我们就能知道每个顶点是什么时候被发现的。
深度优先森林: 有时候,图可能是分开的,比如有两个不同的区域。DFS 会从每一个未访问的顶点开始,形成一个“森林”。就像在一个大森林里,我们可以从不同的树开始爬,每棵树都是一棵新的“深度优先树”。
DFS 的应用:那么,深度优先搜索有什么用呢?它可以用在很多地方: - **迷宫探索**:当你在迷宫中寻找出口时,可以使用 DFS 来找到出路。 - **网页爬虫**:在互联网中,搜索引擎使用类似 DFS 的方法来抓取网页。 - **游戏开发**:很多游戏中都有地图,使用 DFS 可以帮助角色找到路径。 #### 8. 总结 今天,我们一起了解了什么是深度优先搜索(DFS)。它就像在一个迷宫中找到出口的过程,通过不断深入探索直到没有新路径可走,然后再回到之前的点继续探索。
### 课堂讨论:深度优先搜索(DFS)
**场景**:在课堂上,老师和学生围绕深度优先搜索(DFS)进行讨论。学生们通过提问和辩论来加深对DFS的理解。 ---
**学生A**:老师,能不能先给我们简单介绍一下深度优先搜索(DFS)是什么?
**老师**:当然可以!深度优先搜索(DFS)是一种用于遍历或搜索图或树数据结构的算法。它从一个起始节点开始,尽可能深入地访问每个邻接节点,直到没有未被访问的邻居为止,然后回溯到上一个节点继续搜索。🤔
**学生B**:那么,DFS的具体步骤是什么呢?
**老师**:好的,DFS的过程可以分为几个步骤。
让我用一个简单的图来举个例子: ``` A / \ B C | | D E ```
1. **开始访问**:从节点A开始,将其颜色设置为灰色(表示正在访问),并记录发现时间。
2. **访问邻接节点**:接着访问B,将B的颜色设置为灰色,记录发现时间。
3. **继续深入**:然后访问B的邻接节点D,将D的颜色设置为灰色,记录发现时间。D没有未被访问的邻接节点,因此将其颜色设置为黑色(表示已完成),并记录完成时间。
4. **回溯**:回到B,B没有其他未被访问的邻接节点,因此将其颜色设置为黑色,记录完成时间。
5. **返回A**:回到A后,访问C,重复以上过程。 这样,DFS就完成了一次遍历!🎉 ---
**学生C**:老师,DFS和广度优先搜索(BFS)有什么不同之处呢?
**老师**:这是个好问题!DFS是递归的,使用栈来实现,而BFS是使用队列进行层级遍历。举个例子,想象一下你在探索一个迷宫: - **DFS**就像你随便选择一个方向,一直走到尽头,如果碰到墙再回头选择其他路径。 - **BFS**则像你一层一层地探索,先走完一层所有的路径再进入下一层。😄
**学生A**:能不能给我们具体解释一下DFS的颜色标记和时间戳是怎么用的?
**老师**:当然可以!颜色标记和时间戳对于跟踪访问状态非常重要。
### 例子1:颜色标记 - **白色**:表示未被访问。 - **灰色**:表示正在访问。 - **黑色**:表示已完成。 假设我们从A开始,A被标记为灰色,表示我们正在访问它。访问完所有邻接节点后,将A标记为黑色,表示我们完成了对A及其邻接节点的所有访问。这种标记方式可以帮助我们避免重复访问同一个节点。👍
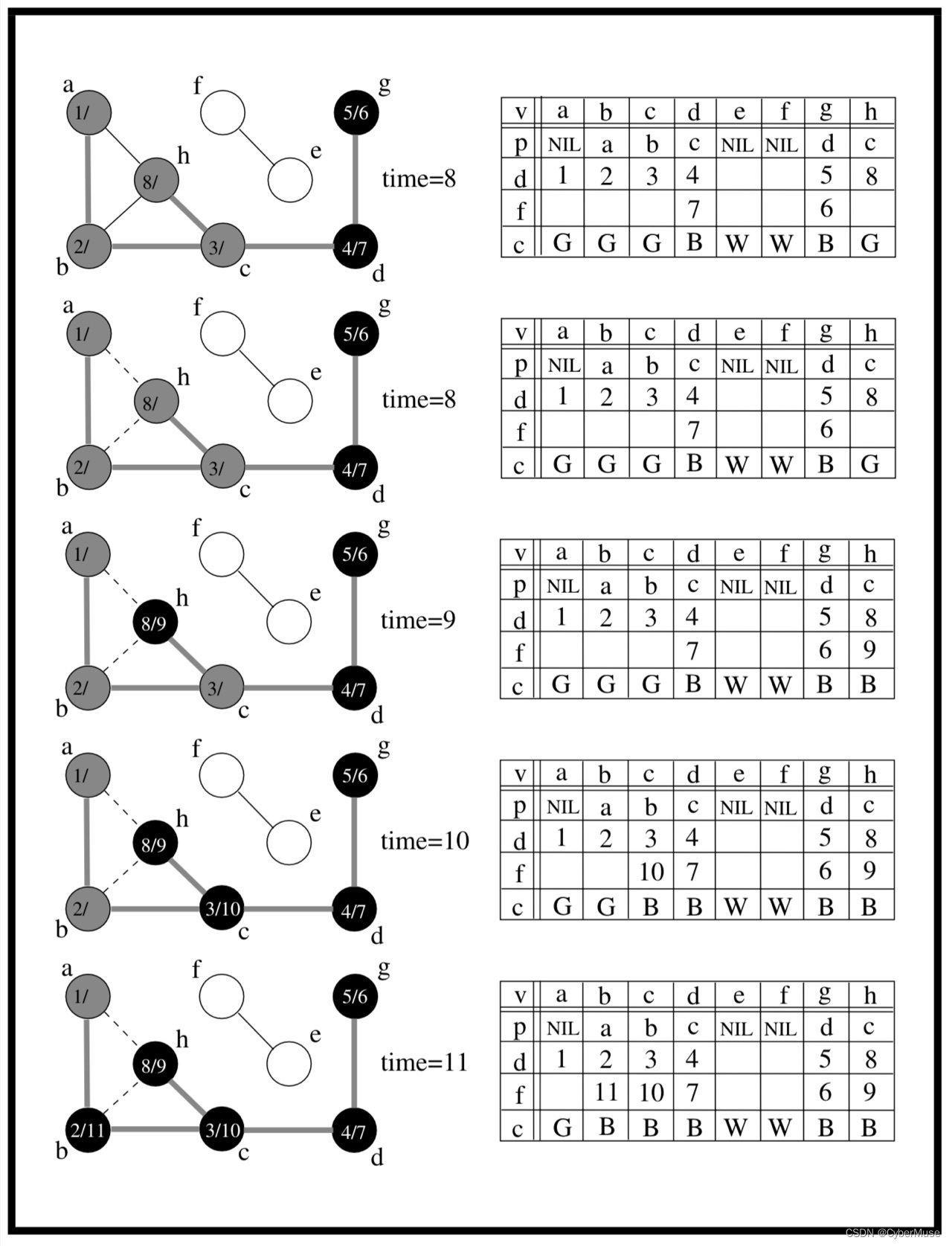
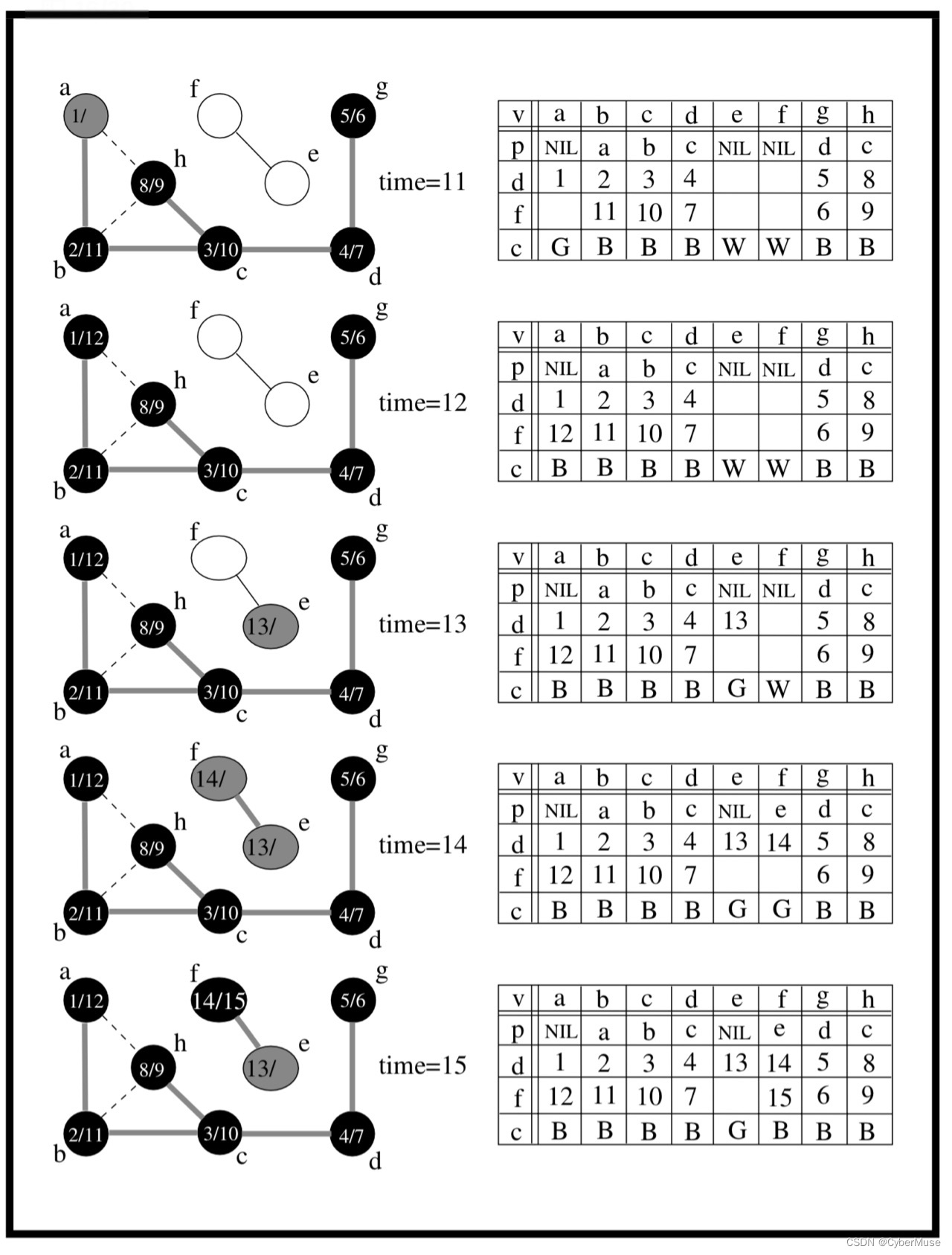
### 例子2:发现时间和完成时间 - **发现时间**:表示节点第一次被访问的时刻。 - **完成时间**:表示节点及其所有邻接节点都被访问完毕的时刻。 比如,当我们访问A时,记录下它的发现时间(例如1),然后继续访问B,记录B的发现时间(例如2),最后访问D,记录D的发现时间(例如3)。当D完成后,我们再回到B并记录B的完成时间(例如4),最后完成A的访问(例如5)。这样,我们就能清晰地跟踪每个节点的访问顺序。🕒
### 例子3:前驱节点 前驱节点帮助我们重建路径。例如,当我们从A访问到B,然后再访问D,D的前驱节点是B,B的前驱节点是A。这样,我们可以从D回溯到A,重建出完整路径。 -
**学生B**:老师,能不能给我们总结一下DFS的优缺点?
**老师**:当然可以!DFS的优点包括:
1. **实现简单**:算法易于实现,特别是在递归时。
2. **内存使用少**:相比BFS,DFS通常使用更少的内存,因为它只需要存储当前路径上的节点。
缺点包括: 1. **可能会陷入死胡同**:在某些情况下,DFS可能会在一个深层的分支中长时间停留,导致效率低下。
2. **不保证找到最短路径**:如果我们寻找最短路径,DFS可能不是最佳选择。
**学生C**:谢谢老师,今天的讨论让我对DFS有了更深入的理解!😄
**老师**:非常高兴你们能参与讨论!记得在实践中使用这些概念,实践是最好的老师!如果还有疑问,随时可以提出来哦!