NLP 经典面试题————Self-Attention 的时间复杂度/空间复杂度是怎么计算的?
本人是某双一流大学硕士生,也最近刚好准备参加 2024年秋招,在找大模型算法岗实习中,遇到了很多有意思的面试,所以将这些面试题记录下来,并分享给那些和我一样在为一份满意的offer努力着的小伙伴们!!!
面试题
Self-Attention 的时间复杂度/空间复杂度是怎么计算的?
标准答案
阅读 Transformer 相关的论文,在讨论 self-attention 的时间和空间复杂度时,都会提到是 O(N^2),其中 N 是序列长度。
关于时间复杂度(time complexity)或空间复杂度 O(·),首先要知道这只是一种定性分析,而不是精确的定量分析。
我们来看下 scaled dot-product attention的时间和空间复杂度:
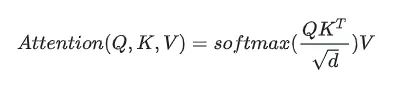
为了分析时间和时间复杂度,我们把上面的计算过程拆分:
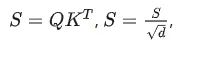
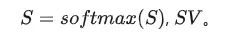
只要我们分析出每个计算的复杂度,就可以得到整体计算的复杂度。
我们先来看第一个矩阵乘法
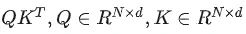
矩阵乘法的朴素算法时间复杂度是
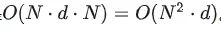
至于空间复杂度,只看存储 计算结果,复杂度是 ,但是也不要觉得这个数字很大,如果 ,其实存储 Q 和 K 要比 更占内(显)存。除非是序列很长 ,空间复杂度 才会是瓶颈。
简单回顾下矩阵乘法
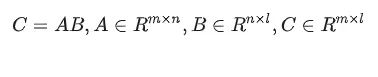
C = np.zeros((m, l)) for i in range(m): for j in range(l): for k in range(n): C[i][j] += A[i][k] * B[k][j]
显而易见,3 个 for 循环,因此矩阵乘法时间复杂度 。
我在网上查找矩阵乘法时间复杂度分析的资料时,发现很多人喜欢用numpy.dot+画图的方式来直观展示,很有趣:
m = 64 n = 64 l = 64 times = [] ms = [] for i in range(20): ms.append(m) begin = time.time() m1 = np.random.random((m, n)) m2 = np.random.random((n, l)) times.append(time.time() - begin) m *= 2 # 改变 m 的大小, 同理可以改变 n 或 l 的大小 # 画图 fig, ax = plt.subplots() ax.set_ylabel('Time') ax.set_xlabel('Array Dimension Size') ax.plot(ms, times) plt.show()
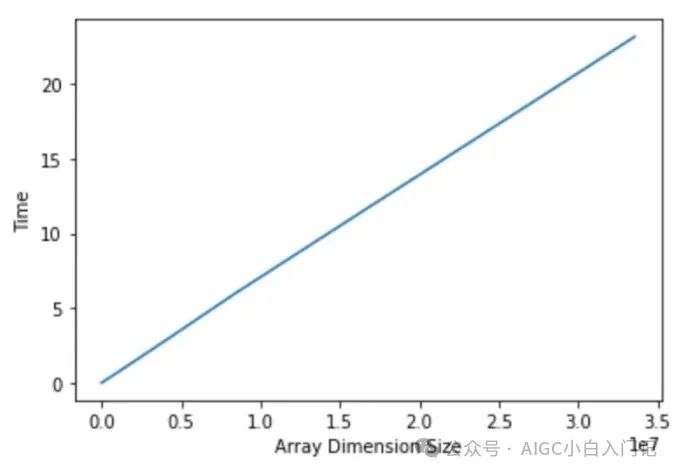
可以看到,矩阵乘法时间和其中 m 维度大小成正相关,斜率 ~1,如果改变 n 或 l 也会得到相同的结论,因此矩阵乘法时间复杂度是 。
由于

因此

的时间复杂度为
我们再来看 softmax 时间复杂度,假设 z 是一维向量:
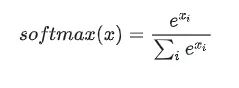
def softmax(x): m_val = max(x) x = [i-m_val for i in x] x = [math.exp(i) for i in x] deno = sum(x) return [item / deno for item in x] softmax([1,2,3]) # [0.0900, 0.2447, 0.6652]
Self-Attention包括三个步骤:相似度计算,softmax和加权平均
-
step1: 相似度计算可以看作大小为(n,d)和(d,n)的两个矩阵相乘:,得到一个 的矩阵.
-
step2: softmax就是直接计算了,时间复杂度为
-
step3: 加权平均可以看作大小为 和 的两个矩阵相乘: ,得到一个 的矩阵
因此,Self-Attention的时间复杂度是 。
这样,整个
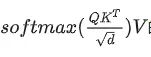
的时间复杂度是:
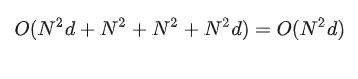
如果把向量维度 d 看作常数,则可以说 self-attention 的时间复杂度是序列长度的平方。
再来看下空间复杂度,不论是存储
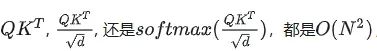
最后存储
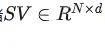
的空间复杂度是
这样,整个空间复杂度可以看作:
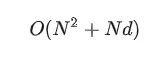
如果把向量维度 d 看作常数,则可以说 self-attention 的空间复杂度是序列长度的平方。
如何学习AI大模型 ?
“最先掌握AI的人,将会比较晚掌握AI的人有竞争优势”。
这句话,放在计算机、互联网、移动互联网的开局时期,都是一样的道理。
我在一线互联网企业工作十余年里,指导过不少同行后辈。帮助很多人得到了学习和成长。
我意识到有很多经验和知识值得分享给大家,故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。【保证100%免费】🆓
CSDN粉丝独家福利
这份完整版的 AI 大模型学习资料已经上传CSDN,朋友们如果需要可以点击下方CSDN官方认证链接免费领取 【保证100%免费】
读者福利: 👉👉CSDN大礼包:《最新AI大模型学习资源包》免费分享 👈👈
对于0基础小白入门:
如果你是零基础小白,想快速入门大模型是可以考虑的。
一方面是学习时间相对较短,学习内容更全面更集中。
二方面是可以根据这些资料规划好学习计划和方向。
👉1.大模型入门学习思维导图👈
要学习一门新的技术,作为新手一定要先学习成长路线图,方向不对,努力白费。
对于从来没有接触过AI大模型的同学,我们帮你准备了详细的学习成长路线图&学习规划。可以说是最科学最系统的学习路线,大家跟着这个大的方向学习准没问题。(全套教程文末领取哈)

👉2.AGI大模型配套视频👈
很多朋友都不喜欢晦涩的文字,我也为大家准备了视频教程,每个章节都是当前板块的精华浓缩。


👉3.大模型实际应用报告合集👈
这套包含640份报告的合集,涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师,还是对AI大模型感兴趣的爱好者,这套报告合集都将为您提供宝贵的信息和启示。(全套教程文末领取哈)

👉4.大模型落地应用案例PPT👈
光学理论是没用的,要学会跟着一起做,要动手实操,才能将自己的所学运用到实际当中去,这时候可以搞点实战案例来学习。(全套教程文末领取哈)

👉5.大模型经典学习电子书👈
随着人工智能技术的飞速发展,AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型,如GPT-3、BERT、XLNet等,以其强大的语言理解和生成能力,正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。(全套教程文末领取哈)

👉6.大模型面试题&答案👈
截至目前大模型已经超过200个,在大模型纵横的时代,不仅大模型技术越来越卷,就连大模型相关的岗位和面试也开始越来越卷了。为了让大家更容易上车大模型算法赛道,我总结了大模型常考的面试题。(全套教程文末领取哈)

👉学会后的收获:👈
• 基于大模型全栈工程实现(前端、后端、产品经理、设计、数据分析等),通过这门课可获得不同能力;
• 能够利用大模型解决相关实际项目需求: 大数据时代,越来越多的企业和机构需要处理海量数据,利用大模型技术可以更好地处理这些数据,提高数据分析和决策的准确性。因此,掌握大模型应用开发技能,可以让程序员更好地应对实际项目需求;
• 基于大模型和企业数据AI应用开发,实现大模型理论、掌握GPU算力、硬件、LangChain开发框架和项目实战技能, 学会Fine-tuning垂直训练大模型(数据准备、数据蒸馏、大模型部署)一站式掌握;
• 能够完成时下热门大模型垂直领域模型训练能力,提高程序员的编码能力: 大模型应用开发需要掌握机器学习算法、深度学习
CSDN粉丝独家福利
这份完整版的 AI 大模型学习资料已经上传CSDN,朋友们如果需要可以点击下方CSDN官方认证链接免费领取 【保证100%免费】
读者福利: 👉👉CSDN大礼包:《最新AI大模型学习资源包》免费分享 👈👈
