
摘要
四旋翼无人机由于其复杂的动态特性和高度耦合的多输入多输出(MIMO)系统,使其控制成为一个具有挑战性的课题。本文提出了一种基于超螺旋滑模控制(ST-SMC)的轨迹跟踪控制算法,以提高无人机的稳定性和精确性。通过仿真实验验证了该方法的有效性,并将其与传统控制方法进行了比较,结果表明ST-SMC控制能够实现更精确的轨迹跟踪,并在干扰和参数不确定性下表现出较强的鲁棒性。
理论
-
无人机动力学模型:四旋翼无人机是一个六自由度的非线性系统,包含平移和旋转运动。其动力学方程如下:ST-SMC设计:
滑模面设计:ST-SMC设计:
滑模面设计:
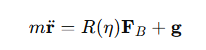
其中,𝑟是无人机的位置,𝑅(η) 是由欧拉角决定的旋转矩阵,𝐹𝐵是无人机在机体坐标系下的推力向量,𝑔是重力加速度。
-
滑模控制原理:滑模控制是一种鲁棒控制方法,能够处理系统中的不确定性。超螺旋滑模控制在传统滑模控制基础上进一步增强了系统的收敛速度和控制精度。
-
ST-SMC设计:
-
滑模面设计:
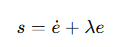
其中
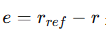
是位置误差,λ 是正的常数。
-
控制律:
![]()
其中 𝑘 1 , 𝑘 2 为设计参数,用于控制系统的滑模面到达速度和滑动模态的鲁棒性。
实验结果
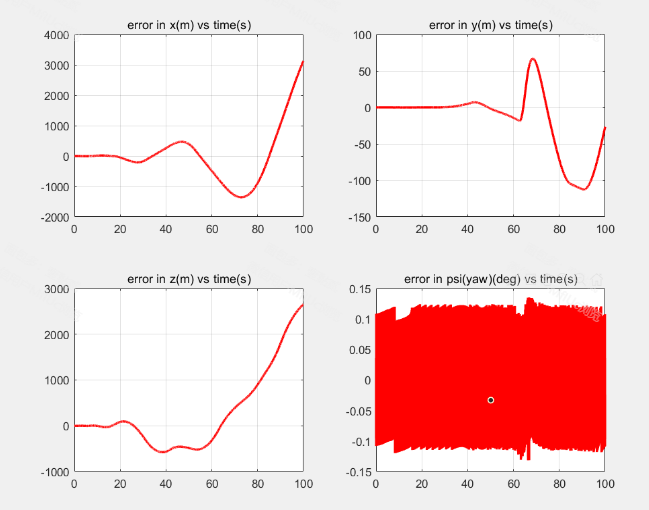
从仿真图可以看出,ST-SMC算法能够在较短时间内有效地跟踪参考轨迹。误差曲线图(图一)显示了在不同方向上的位置和姿态误差。比较图(图二)则展示了参考轨迹与实际测量轨迹的匹配度。可以观察到,ST-SMC在干扰存在时仍能保持较小的跟踪误差,尤其在 z 方向和姿态控制上具有较强的鲁棒性。

部分代码
以下为部分ST-SMC控制算法的实现代码:
% 超螺旋滑模控制的部分实现
function u = st_smc(e, de, lambda, k1, k2)% 滑模面设计s = de + lambda * e;% 控制律u = -k1 * sign(s) - k2 * sign(diff(s));
end
参考文献
❝
Slotine, J. J. E., & Li, W. (1991). Applied Nonlinear Control. Prentice-Hall. 2.Utkin, V. I. (1977). Sliding Modes in Control Optimization. Springer.
Khalil, H. K. (2002). Nonlinear Systems (3rd ed.). Prentice-Hall.

