声明:本人跟随b站江科大学习,本文章是观看完视频后的一些个人总结和经验分享,也同时为了方便日后的复习,如果有错误请各位大佬指出,如果对你有帮助可以点个赞小小鼓励一下,本文章建议配合原视频使用❤️
如果你也正在学习STM32可以订阅本专栏,后续将不定期更新( ˘ ³˘)❤️
如有侵权,请私信联系删除
文章目录
- 前言
- 理论部分
- 1.PID基本原理
- PID简介
- 开环与闭环
- 2.PID算法原理
- 比列项
- 积分项
- 微分项
- 3.离散PID&程序实现思路
- 连续和离散形式PID
- 位置式PID和增量式PID
- PID程序实现
- 4.常见优化算法方法
- 积分限幅(只用于位置式)
- 积分分离(定位置)
- 变速积分
- 微分先行
- 不完全微分
- 输出偏移
- 输入死区
- 注意事项
- 5.双环PID基本原理
- 串级PID简介
- 单双环对比
- 6.调参技巧
- 代码部分
前言
- 这一块的学习还是得有实践,不亲自感受一下pid调参那么无异于没学
- 想要制作平衡车的小伙伴建议再去学习一下姿态解算也是很有趣的
- 了解PID每一项的作用以及计算方式很重要
- 优化算法一定要根据实际情况来,不然容易起到反效果
- 串级PID的优点和建立方法要理解
- 调参要懂取舍,多调参才能积累经验
理论部分
1.PID基本原理
PID简介

- 做小车就会用到PID算法,因为小车想要走直线就要保证两个轮子PWM输出的占空比一致,不一致小车就会走不直,可是你若只考虑输出相同的占空比,但是还会存在润滑油多少等外力因素,导致两个轮子速度肯定不一样,这时候为了保证速度相同就要使用PID算法
开环与闭环

- 闭环相较于开环相当于多了一个反馈电路形成闭合环路,可根据反馈不断调节输出值来接近目标值,开环不会自己调节,输出一个值后就定死了,哪怕被控对象受外部因素而偏离目标值,输出值仍然不会自我调整
2.PID算法原理

- 看这个图就知道PID是一种基于误差调控的算法,PID的目的是让误差为0
- 第二个输出值公式更为常用,因为分别调节三个参数可以改变三项的值,便于调参,Kp,Ki,Kd是每一项的权重
比列项

- Kp*error(t)就是系统调控的力度,假如error(t)=10,单位可能是速度转速等等,那么Kp给0.1的话,调控力度就是1,给1的话力度就是10,依次类推,所以Kp不能太大了,否则误差只要变化很小,比列这一项就会猛的一调,也就是超调,太小的话也不行系统响应会很慢
- 但是不能只有比列这一项用于调节输出值,会存在稳态误差

- 红色线条表示电机目标速度,紫色线条是电机实际速度
- 红色框框表示超调,蓝色差值表示稳态误差,稳定后的实际速度与目标速度的差值
- 这个图就是只看P比例项的波形图,可以看到Kp越大红色框框的超调就越大
- 按理来说只要存在误差P就会一直进行调节,那为什么会有稳态误差呢?先看看下面对稳态误差的介绍
稳态误差
- 在理想情况时不存在稳态误差,但是由于电机旋转必然存在摩擦力,PID最终目的是误差为0,但是误差为0时我们的P项输出也为0,PID的输出结果直接送到了PWM的输出函数,也就是PWM输出为0了,电机也就没有驱动力不在转动,由于摩擦力肯定会减速,一旦减速就会有误差,PID又要开始加速,也就是PWM输出又会增加,驱动力也会增加,直到驱动力等于摩擦力时系统达到稳态
可能有人会问当驱动力和摩擦力达到平衡时,稳态的值还没达到目标值,难道系统系统看不到吗,不会继续增大PWM吗?但是由于P项过后误差已经很小了,算法得出的结论是我提供这么多驱动力就够了,但是系统不知道有摩擦力这么个东西,导致提供的驱动力一直达不到目标值,也没人告诉他驱动力已经和摩擦力平衡了需要继续增大驱动力,所以才需要其他项来帮助PID算法- 积分项就是用于帮助消除稳态误差的,因为比列项输出值仅取决于当前误差,与历史时刻误差无关,这意味你想实现使用当前误差产生的占空比,并在此基础上加上比例项的输出作为新的占空比(这样误差为正必然加大占空比加速,为负必然减小占空比减速)是行不通的,或者说这其实是积分项的任务
积分项

- 积分项用于消除稳态误差,也就是提醒系统你的驱动力用来平衡摩擦力了,还得更努力增大驱动力才能达到目标值
- 写积分项程序要单独定义一个变量存储历史误差,误差不断累计并求和然后乘以一个积分系数得到积分项的输出
- 积分项不断累积使其控制力度越来越大,直到能够让电机占空比变大,最终达到目标值消除稳态误差
积分项的弊端就是系统滞后性:也就是当系统稳态误差消除后,此时突然要求电机反转,那么先要不断反向积分来消除正向的驱动力,然后再继续累计使其反转- 比列项相对于积分项来说变化非常快,因为只用考虑当前时刻,你说正就是正,你说负就是负,系统响应很快
微分项

- 微分项不会消除误差
- 主要作用是防止超调,阻止变化过快,提前调控
- 打个比方,平衡车如果只有PI项很难稳定立起来,因为倒下太快了,PI来不及做出调整让重新平衡,D项的作用就是让他到下更慢一点,这是PI有更多时间调整
- 缺点就是微分系数过大时会卡顿,因为D项权重太大,导致PI想发生变化时,D项想让变化慢一点,阻止了PI产生的变化,导致卡顿
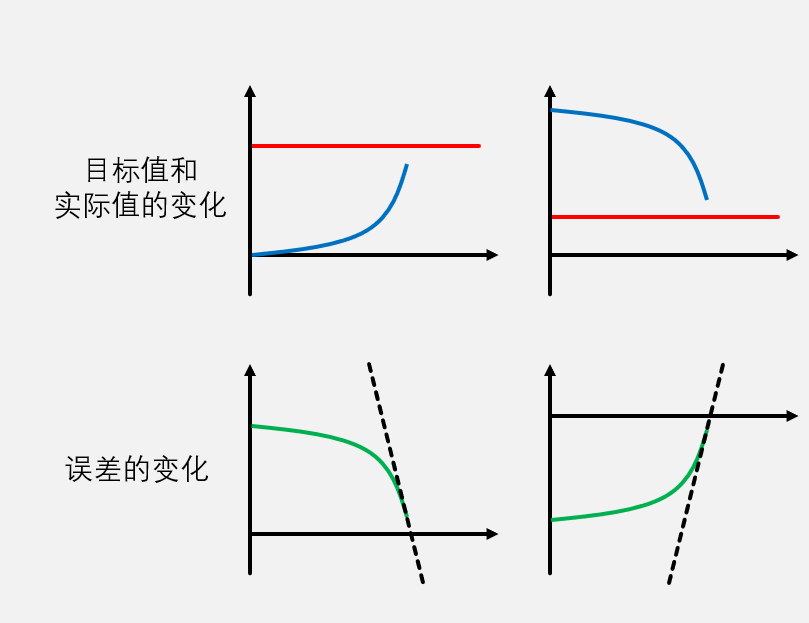
- 蓝色曲线为实际值,红色为目标值,绿色为误差值(红色-蓝色)
- 上面两个中蓝线都是越接近目标值变化越快,这种就一定要加D项
- 下面两个图也能看出来误差变化太快需要D项帮助

这就很明显了,第一个图中只有PI作用,那么每当有误差时,PI的调节就会超调导致误差更大,越调越超调,离目标值越来越远,但是加上D项之后就发现会离目标值越来越近,而且微分系数越大阻尼越大,阻尼振荡越来越小
3.离散PID&程序实现思路
连续和离散形式PID

- 连续PID需要用模拟电路实现,不断进行计算和调控
- 离散PID则是一个周期进行一次PID计算和调控
对离散形式PID的理解:- 比例项:这里的k表示第k次调控,P项也就是比例系数乘以第k次的调控时刻的误差
- 积分项:看下面这个图就是连续和离散化的区别,第一个图就是积分的定义,其实就是蓝色矩形面积之和,T就是宽(T越小求和越准确),error(j)就是长,乘积就是面积,j是一个临时变量用于使用循环求和
- 微分项:某一点的微分就是斜率,这里也是使用两点来计算斜率,T也是越小计算结果越精准

位置式PID和增量式PID

- 位置式PID能够应用于各种场景
- 增量式PID其实就是相邻两次PID之间的差值

- 两者的区别:位置式可直接给被控对象,增量式需要被控对象有积分功能,也就是需要被控对象拥有记录上一次状态的功能,才能在此基础上根据增量改变
- 两者直接皆可以实现相互转化
- 位置式PID输出的得到的是全量输出值,如果有噪声干扰,不同输出值相差会很大,导致执行机构大幅度变化;增量式PID则可以单独对输出值增量进行限幅,防止执行机构大幅度变化
- 增量式PID适合自动控制和手动控制切换的场景,自动控制也就是使用PID,手动控制也就是不使用PID,当你将三个参数全部给0时就是自动控制,这个时候如果是位置式电机会由于参数为0输出值也立马变为0,点击停转,但是增量式具有存储上一个输出量的功能,输出值可以位置在当前值所以不会停,这个时候就可以手动调节输出值
PID程序实现
首先确定周期T的值,不能太快也不能太慢,太慢起不到平衡作用,太快硬件传感器分辨率受限,以下是三种实现每隔时间T实现一次PID调控的方法
第一个方法最简单但是阻塞式弊端太多;第二个方法定时中断一般最常用,但是要注意不能在中断和主函数里操作同一个硬件,避免资源访问冲突; 第三种也是定时中断,但是自定义标志位可以在主函数里执行PID调控,该方法主程序一定不能阻塞了
位置式PID程序的实现思路
- 输出限幅是因为怕PID的输出值超过了硬件的接受范围,所以设置一个接受的上下限
增量式PID程序的实现思路
- 这里是控制器内积分得到out而不是out的增量
4.常见优化算法方法

积分限幅(只用于位置式)

- 造成原因:断电或者电机卡死等原因会使电机的实际速度为0,和目标值相差过大,导致积分项会一直无限制积分,而此时一旦又通电,由于积分项太大了电机会满速运转,直到积分项反向积分使电机转速实际值与目标值重合,此时改变目标值才会有效果,在此之前无论如何修改目标值都没用。
电机通电满速运转一段时间且无法控制是危险的 - 实现思路:限制误差积分的增大上限,也就是哪电机停转了,也不能让积分项一直增大,而是增大到一定值就停止增大
- 阈值设置:最大阈值也就是让积分项=最大输出值,此时误差积分=最大out值/Ki

积分分离(定位置)

- 常见的都是定速使用PI,定位置用于PD就够了,当定位置使用PD时会发现实际值与目标值总会有那么一点点误差无法消除,是因为理论上只要有PWM电机就会动,但是实际上有摩擦力,PWM很小时驱动力只能够平衡摩擦力,推不动电机旋转,导致一点点的稳态误差,我们也知道积分项可以用来消除稳态误差,实际上确实可以,但是用于定位置控制时又会出现更大的问题——超调,而且这个超调微分项不能解决
- 使用积分项的超调原因:理论上定位置不存在稳态误差,因为摩擦力基本可以忽略不计,我们只使用比例项完全就够用了,因为定位置最后OUT输出值也为0,电机不旋转,也就是比例项的输出值刚好就是整个OUT输出值(OUTp=OUT),此时加上积分项后,就会是OUTp+OUTi>OUT,这就会导致超调,实际图像就是下图所示,会先超过目标值,然后此时比例项迅速反应并进行反向积分,积分项会迅速反向积分,当积分项正向积分与反向积分抵消时,此时比例项才会使误差为0

- 解决方法:当误差大时使用PD,误差很小时使用PID,防止积分项一直积分导致驱动力不可避免的过大导致超调,如果只在后半段接近目标值才积分,积分时间很短,积分项很小不会产生过大驱动力导致超调

- 分离阈值的设置:使用外力施加于电机并观察波形,使用较大外力时,此时误差会很大,此时阈值比误差值大一点就行,太小了会导致当外力迅速变化时积分项迅速为0,导致此时无积分项来抗衡外力;太大了会导致积分项还是太大了导致超调
变速积分

- 变速积分其实就是积分分离的升级版,积分分离是只存在有积分项和无积分项两种情况,变速积分则是积分项大小会随误差大小变化而变化,麻烦的是需要设置一个函数表示变化关系,如果函数不好的话,效果甚至不如积分分离


微分先行


- 当目标值突然变化时,微分项是误差的斜率,也就是起初微分项接近正无穷大,后面误差变化正常,斜率是负的反向微分而且微分项会越来越小

- 目标值频繁切换导致数据产生尖峰,且Kd越大尖峰越高,按理来说只存在微分项时,只改变目标值电机不会旋转,因为微分项只起到给实际值添加阻尼效果,应该不具备输出能力,但是实际上纯微分项控制时电机会由于误差快速变化导致旋转,那么其实可以只对实际值进行微分,无论误差如何变化,此时微分项就只起到加阻尼效果而不具备输出能力,而且实际值也不会突变。在计算误差进行PI之前提前对实际值进行微分,这就是微分先行的原理
但是实际情况要看使不使用微分先行,因为微分项可以帮助比例项更快响应目标值变化,尤其是误差较大的变化,如果只需要微分项起到阻尼效果可以加微分先行

不完全微分


- 观察上面的图,红色曲线代表噪声,绿色曲线是理想值,噪声对比例项来说影响很小,就是噪声和理想值的误差值之差,一般噪声和理想值不会相差很大;对积分项来说就是曲线下的面积,噪声有时候比理想值高有时候也有低的时候,所以实际面积两者相差不大;微分项代表斜率,看图可知理想值的斜率为正的时候,噪声可能直接为负值了,这个影响就很大,所以需要过滤噪声也就是添加滤波器,也就是不完全微分
- 之所以不对开始的值全部滤波,是因为滤波会增加时延,导致PID响应速度变慢
- 不完全微分的微分项就是本次微分项和上次微分项占不同权重然后加起来得到新的微分项,a取0.5相当于均值滤波,a越大本次微分项权重越低,滤波效果就越好
- 一阶惯性单元滤波公式:假设输入是x(k),输出是y(k),则有y(k)=(1-a)x(k)+ay(k-1),意思是本次输出为本次输入和上次输出的加权平均值

输出偏移

- 也就是PWM要么就不输出,一旦输出,该PWM就一定要能驱动电机
- 偏移量需要单独写一个测试程序测量
- 缺点就是很难稳定,因为PID但凡调控电机必定转动,目标值与实际值会一直存在误差很难为0,甚至目标值都在抖动有噪声,所以就会一直抖动

输入死区

- 死区阈值

注意事项
- 积分限幅一般都要使用
- 微分项可以帮助比例项更快响应目标值变化,尤其是误差较大的变化,如果只需要微分项起到阻尼效果可以加微分先行
- 输出偏移+输入死区可以将误差控制在可接受范围,但是积分分离可以无误差,但是会有积分项的滞后性
- 滤波有延时性,滤波效果越好延时一般越严重
5.双环PID基本原理
串级PID简介

- 关键所在:使用外环PID的输出值作为内环PID的目标值,但是内外环的PID的实际值都会返还给当前环
- 可以对更多物理量进行控制,性能更好,比如可以实现点击定速定位控制,也就是让电机以指定速度来到指定位置停下来
单双环对比

- 双环PID相当于单环PID自带一个定速控制的电机,而且位置环想控制位置时输出一个值给速度环,当实际位置与目标位置越接近时,位置环输出越小,速度环目标速度也就越小直到为0,此时电机达到指定位置而且速度也为0
- 不存在启动力度过小电机转不起来的问题,因为位置环的目标位置设置很小时输出值给到了PI控制的速度环,由于是PI控制那么只要有目标速度而且目标位置与实际位置存在误差电机一定为转动而且最终会与目标位置重合
- 抵抗外力的作用更强,因为施加外力时,速度环的目标速度应该为0,却由于外力产生实际速度,有了误差就会PI调控产生一个阻力对抗外力,而且又存在位置环,施加外力导致位置改变,位置环又要产生负向输出值给到速度环,让速度环的误差变大,速度环的积分项就会更大从而产生更大的对抗力
- 优点也就是响应速度快,稳定性好,准确性高
- 调参顺序:先内环后外环

- 内环和外环调控周期可以不同,可以设计总PID调控周期,然后在里面分别设置内环外环的调控周期
一般外环调控周期大于或等于内环,一是因为外环输出值刷新很快内环读取不过来没什么意义,二是因为内环一般调控反应更快的物理量,频率更大- 需要修改内环PID的积分阈值,为外环的目标值的阈值,然后加上InnerTarget=OuterOut
- 修改内环参数时,先要取消外环对内环的控制,也就是注释这一句InnerTarget=OuterOut
- 修改内环的速度可以修改内环数值的积分限幅幅值
6.调参技巧
- Kp:不断改变目标值观察实际值,然后逐步增大Kp直到实际值开始抖动,然后适当减小KP让抖动消失,此时Kp就比较适合
- Ki :看消除稳态误差的速度不满不满意,不满意就加大Ki但是不能够出现大幅度超调
- Kd:太大会出现振荡,调节PD时,可以将P参数给大一点也没啥,超调可以用D来调节但是不能振荡,如果振荡就要调小KP
- 三个参数的值建议量程显示大一点,尤其是使用电位器时候由于电位器的抖动,三个参数并不能完全为0,会出现实际值仍然缓慢跟踪目标值,量程够大的话能够看见应该不是0
- 学会取舍,参数越响应快但是抖动振荡越严重,参数小响应慢但是动作平滑
代码部分
PID.c
#include "stm32f10x.h" // Device header
#include "PID.h"void PID_Update(PID_t *p)
{p->Error1 = p->Error0;p->Error0 = p->Target - p->Actual;if (p->Ki != 0){p->ErrorInt += p->Error0;}else{p->ErrorInt = 0;}p->Out = p->Kp * p->Error0+ p->Ki * p->ErrorInt+ p->Kd * (p->Error0 - p->Error1);if (p->Out > p->OutMax) {p->Out = p->OutMax;}if (p->Out < p->OutMin) {p->Out = p->OutMin;}
}PID.h
#ifndef __PID_H
#define __PID_Htypedef struct {float Target;float Actual;float Out;float Kp;float Ki;float Kd;float Error0;float Error1;float ErrorInt;float OutMax;float OutMin;
} PID_t;void PID_Update(PID_t *p);#endif












