活动宣传推广的形式有哪些_成都专门做网络推广的公司_如何提升网站seo排名_企业培训课程表

引入

先介绍几个概念

1.公平组合游戏ICG：

• 两名玩家交替行动
• 在任意时刻，可执行的行动与玩家本身无关（游戏公平性）
• 不能行动的玩家输

2.有向图游戏

• 给定一个有向无环图，具有唯一的起点，玩家交替的把棋子沿有向边进行移动，每次移动一步，无法移动者输
• 任何ICG均可化为有向图游戏

3.先手必胜与先手必败

• 在双方均完全理性的情况下，先手不必胜则必败，先手不必败则必胜

NIM游戏：

1.介绍

NIM 游戏是一种经典的组合博弈，两名玩家轮流从若干堆石子中选择一堆，并从中取走任意数量的石子。无法继续操作的玩家判负。

2.结论

对于 $n$ 堆石子 $a_1,a_2,\cdots ,a_n$

• 先手必胜态：$a_1\oplus a_2\oplus a_3\oplus \cdots \oplus a_n\ne 0$
• 先手必败态：$a_1\oplus a_2\oplus a_3\oplus \dots \oplus a_n=0$

3.证明：

通过数学归纳，从特殊推向一般。

1. 不能操作时，每堆都是 0，$0\oplus 0\oplus \dots \oplus 0=0$

2. 当 $a_1\oplus a_2\oplus \dots \oplus a_n=0$，任意一步操作之后 $a_1^{\prime }\oplus a_2^{\prime }\oplus \dots \oplus a_n^{\prime }\ne 0$

   反证：对任意一步操作使 $a_i\to a_i^{\prime }$

   若 $a_1\oplus a_2\oplus \dots \oplus a_i\oplus \dots \oplus a_n=0$，$a_1\oplus a_2\oplus \dots \oplus a_i^{\prime }\oplus \dots \oplus a_n=0$

   设 $a_1\oplus a_2\oplus \dots \oplus a_i\oplus \dots \oplus a_n=x\oplus a_i=0$

   则 $a_1\oplus a_2\oplus \dots \oplus a_i^{\prime }\oplus \dots \oplus a_n=x\oplus a_i^{\prime }=0$

   则 $x=a_i=a_i^{\prime }$，但是 $a_i\ne a_i^{\prime }$，矛盾！得证。

3. 当 $a_1\oplus a_2\oplus \dots \oplus a_n\ne 0$，一定存在一步操作之后 $a_1^{\prime }\oplus a_2^{\prime }\oplus \dots \oplus a_n^{\prime }=0$

   证明：设 $a_1\oplus a_2\oplus \dots \oplus a_n=x\ne 0$，设 $x$ 的最高位 1 在第 $k$ 位。

   则 $a_1,\dots ,a_n$ 中必定存在至少一个 $a_i$ 的第 $k$ 位也为 1，且 $a_i\oplus x<a_i$

   （若第 $k$ 位均为 0，则所有异或之后得到 $x$ 的第 $k$ 位也只能是 0，不合题意）

   所以可以从 $a_i$ 中拿走 $a_i-(a_i\oplus x)$ 个石子（上一步证明了此步的合法性），使得 $a_i^{\prime }=a_i\oplus x$

   故 $a_1\oplus a_2\oplus \dots \oplus a_i^{\prime }\oplus \dots \oplus a_n=a_1\oplus a_2\oplus \dots \oplus a_i\oplus x\oplus \dots \oplus a_n=x\oplus x=0$，得证。

4. 所以在双方绝对理性的情况下，某一方拿完之后达到了异或值为 0 的情况后，会一直握住这个状态，保证自己必胜。

更详细的思路构造过程及证明请看编程之美_1.11 NIM（1）一排石头的游戏在线阅读

SG函数

1. Mex 运算：

设 $S$ 表示一个非负整数集合，定义 mex(S) 为求出不属于集合 $S$ 的最小非负整数的运算。

即：$\text{mex}(S)=\min (x),x\in N\text{ 且 }x\notin S$

2. SG 函数

将游戏的所有状态及其转换关系抽象成一张有向无环图。

定义 $SG(\text{终点})=0$，$SG(x)=\text{mex}[SG(y_1),SG(y_2),\cdots ,SG(y_k)]$

示例：

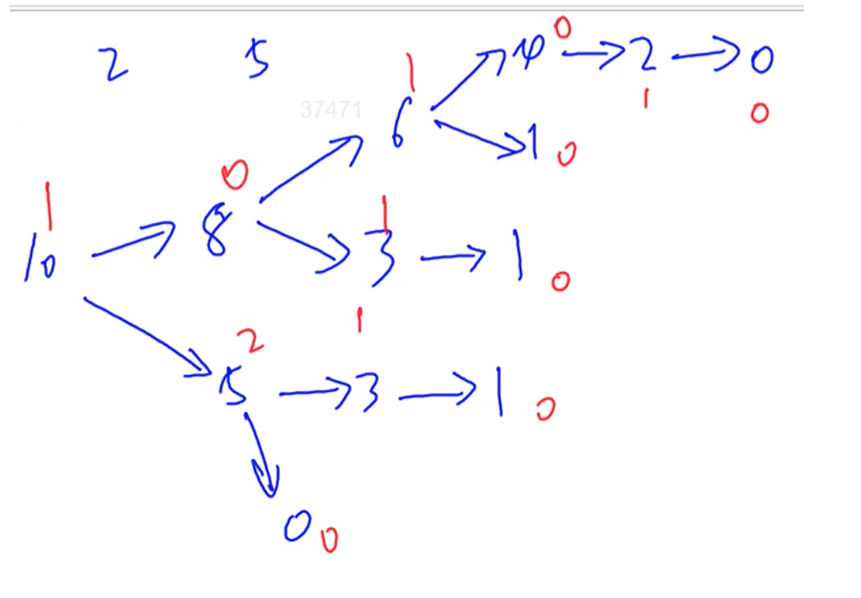
图中模拟一堆个数为 10 的石子的状态转移图，每次只能拿 2 个或 5 个石子，蓝色字为石子数，红色字为对应状态的 SG 值。

由图：任何一个非 0 状态都可以到 0，任何一个 0 状态都到不了 0。

则 $SG(x)=0$ 时，先手拿完后 $SG(x^{\prime })\ne 0$，对手总有办法后手让 $SG(x^{\prime \prime })=0$，先手必败。

$SG(x)\ne 0$ 时，先手总有办法拿完使 $SG(x)=0$，对手怎么拿都使 $SG(x^{\prime \prime })\ne 0$，先手必胜。

性质：$SG(b_1,b_2)=SG(b_1)\oplus SG(b_2)$

对一个含多个图的游戏，取每个图起点 $x_i$ 的 SG 值 $SG(x_i)$

则必胜，当 $SG(x_1)\oplus SG(x_2)\oplus \cdots \oplus SG(x_n)\ne 0$

必败，当 $SG(x_1)\oplus SG(x_2)\oplus \cdots \oplus SG(x_n)=0$

3.证明：

类似一般 NIM 游戏。

1. 当 $SG(x_i)=0$，没有必胜的起点，则 $xor=0$，必败。

2. 存在 $SG(x_i)\oplus x<SG(x_i)$，则我先手一定可以走一步到达 $SG(x_i^{\prime })=SG(x_i)\oplus x$，此时 $xo{r}^{\prime }=0$，对方先手必败，即我方必胜。

3. 当 $xor=x=0$ 时，$SG(x_i)$ 不全为 0 的情况，不管怎么走，$xo{r}^{\prime }\ne 0$，必将落入对方先手必胜局面，即我方必败。

分类

NIM博弈的内容大致就这么多啦~

来几道题目练练手，看看题目中是怎么变形的。

基础变形

洛谷P1247 取火柴游戏

洛谷P7589 黑白棋
$\Rightarrow$ 关键在翻译题目，本质就是简单的 NIM 游戏。

洛谷P5675 取石子游戏 $\Rightarrow$ 背包DP + 阶梯NIM，代码不难理解，关键是想明白思路，考思维

阶梯 Nim

洛谷P3480 KAM-Pebbles $\Rightarrow$ 差分数组的阶梯nim

洛谷P2575 高手过招