好大夫在线医生免费咨询_网页设计与制作思考建议_广州市疫情最新_网站建设公司推荐

一、激活函数

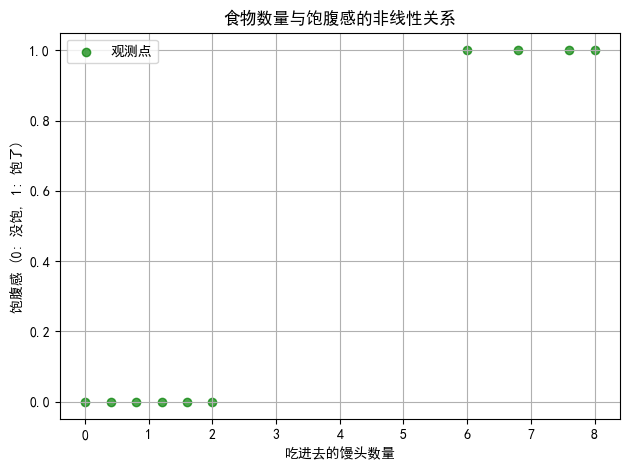
在线性回归中，假设以一种植物的环境温度与生长高度为背景来进行的，因为假设植物的生长高度与环境温度在某种条件下是存在着线性关系的，比如在某个温度范围内，温度越高，植物生长的越高。事实上还有一些情况是无法通过线性关系来描述的，比如在吃饭时，随着吃进去的食物的重量的增加，会逐渐的吃饱，感觉像是有线性关系，可实际上，一般只会根据吃进去食物的数量（例如馒头）来判断是否吃饱，换句话说，进食的结果往往只有饱和没饱两种，如下图所示：

横坐标代表吃进去馒头的数量，纵坐标表示饱腹感，其中0代表没饱，1代表饱了。当希望根据这些数据来判断一个人吃多少食物才能吃饱时，就无法通过一条直线来拟合了，因为图像中的点很明显不是在一条直线的周围，因此使用直线的话，会导致损失函数的值永远也降不下来。既然直线无法拟合这样的点，那么需要一条曲线，通过曲线来拟合这些点，从而能根据该曲线来判断一个人进食食物时对应的饱腹感。

二、前向计算

想要用一条直线变化成曲线来拟合这些散点，在没有直线变曲之前，使用直线是无法拟合这些点的。即使使用y=wx+b来表示，这始终是线性的，不能够很好的表示这种变化。

三、Sigmoid激活函数

想要将直线转换成曲线，可以在直线一个激活函数。激活函数是神经网络中一种重要的非线性函数，其作用在于引入非线性特性，使得神经网络能够学习和表示更加复杂的数据模式和关系。激活函数通常在每个神经元的输出上应用，将输入信号转换为输出信号。

将y=wx+b代入得：

以下是激活函数的主要作用：

1. 引入非线性特性：如果在神经网络中只使用线性变换，例如线性加权和求和，那么整个网络的组合效果将仍然是线性的。激活函数的非线性特性能够在每个神经元上引入非线性转换，从而让神经网络能够学习和表示更加复杂的函数和数据模式。

2. 解决分类问题：在机器学习中，很多任务都是分类问题，即将输入数据映射到不同的类别。激活函数的非线性特性使得神经网络能够学习非常复杂的决策边界，从而更好地解决分类问题。

3. 提高模型的表达能力：激活函数的引入增加了神经网络的表达能力，使得网络可以逼近任何复杂的函数，这种特性称为“普遍逼近定理”（Universal Approximation Theorem）。

4. 反向传播：在神经网络的训练过程中，梯度下降等优化算法通过反向传播来更新网络参数。激活函数的可微性是实现反向传播算法的关键，因为它们允许计算网络中每个神经元的梯度。综上所述，激活函数在神经网络中扮演着非常重要的角色，它们的引入使得神经网络具备非线性表达能力，从而能够处理和解决更加复杂的任务。

四、损失函数

五、反向传播

六、设计思路

6.1、散点输入

import numpy as np
data = np.array([[0.8,0],[1.1,0],[1.7,0],[3.2,1],[3.7,1],[4.0,1],[4.2,1]])
x_data=data[:,0]
y_data=data[:,1]
x_train=np.array(x_data)
y_train=np.array(y_data)

6.2、激活函数

def sigmoid(x):return 1/(1+np.exp(-x))

6.3、参数初始化

w=0
b=0
learing_rate=0.5

6.4、前向传播

z=w*x_train+b
a=sigmoid(z)

6.5、反向传播

de_da=-2*(y_train-a)
da_dz=a*(1-a)
#w
dz_dw=x_train
de_dw=np.mean(de_da*da_dz*dz_dw)
#b
dz_db=1
de_db=np.mean(de_da*da_dz*dz_db)

6.6、完整代码

import numpy as np  
from matplotlib import pyplot as plt  # 定义输入数据和目标输出  
data = np.array([[0.8, 0], [1.1, 0], [1.7, 0], [3.2, 1], [3.7, 1], [4.0, 1], [4.2, 1]])  
x_data = data[:, 0]  # 从数据中提取特征（食物数量）  
y_data = data[:, 1]  # 从数据中提取标签（饱腹感）  # 将数据转为训练数据  
x_train = np.array(x_data)  
y_train = np.array(y_data)  # 激活函数 (Sigmoid)  
def sigmoid(x):  return 1 / (1 + np.exp(-x))  # Sigmoid 函数的公式  # 参数初始化  
w = 0  # 权重初始化  
b = 0  # 偏置初始化  
learning_rate = 0.5  # 学习率（步长）  # 创建图形和子图  
fig, (ax1, ax2) = plt.subplots(2, 1)  # 2行1列的子图  
epoch_list = []  # 用于记录每次迭代的 epoch  
loss_list = []  # 用于记录每次迭代的损失值  # 开始迭代训练  
for i in range(1, 1001):  # 前向传播  z = w * x_train + b  # 计算线性组合  a = sigmoid(z)  # 应用激活函数得到预测值  # 反向传播  de_da = -2 * (y_train - a)  # 计算损失对激活值的导数  da_dz = a * (1 - a)  # Sigmoid 的导数  # w 的梯度计算  dz_dw = x_train  # 对于每个样本，x 是计算 w 的梯度  de_dw = np.mean(de_da * da_dz * dz_dw)  # 计算 w 的更新量  # b 的梯度计算  dz_db = 1  # 偏置对前向传播的影响  de_db = np.mean(de_da * da_dz * dz_db)  # 计算 b 的更新量  # 更新参数  w = w - learning_rate * de_dw  # 更新权重  b = b - learning_rate * de_db  # 更新偏置  # 重新计算预测值和损失  z = w * x_train + b  a = sigmoid(z)  loss = np.mean((y_train - a) ** 2)  # 计算均方误差损失  # 记录每个 epoch 的信息  epoch_list.append(i)  loss_list.append(loss)  # 每 100 次迭代或者第一次迭代时打印损失并更新图表  if i % 100 == 0 or i == 1:  print(i, loss)  # 打印当前迭代数和损失值  # 绘制决策边界  x_min = x_data.min()  # 计算 x 的最小值  x_max = x_data.max()  # 计算 x 的最大值  x_values = np.linspace(x_min, x_max, int(x_max - x_min))  # 生成用于绘图的 x 值  y_values = np.round(sigmoid(w * x_values + b), 3)  # 计算对应的预测值并取整  # 绘制散点图和决策边界  ax1.clear()  ax1.scatter(x_train, y_train)  # 绘制训练数据散点  ax1.plot(x_values, y_values, c='r')  # 绘制决策边界  # 绘制损失曲线  ax2.clear()  ax2.plot(epoch_list, loss_list)  # 绘制每次迭代的损失  plt.pause(1)  # 暂停以便可视化更新  # 显示最终图形  
plt.show()

6.7、设计思路

数据准备：首先定义训练数据，其中包含特征（食物数量）和目标标签（饱腹感）。
参数初始化：初始化权重 w 和偏置 b，并设置学习率。这些参数将在训练过程中不断更新。
向前传播：

计算线性组合 z 并通过 sigmoid 激活函数生成预测值 a。
反向传播：

计算损失函数关于激活值的梯度，进而得到损失函数关于权重和偏置的梯度。
参数更新：使用学习率对权重和偏置进行梯度下降更新。
损失记录与可视化：

每经过一定的迭代次数（例如每100次），输出当前损失值，并更新图表以可视化决策边界和损失变化。
可视化：最后输出散点图和损失变化曲线，使用户可以观察到模型训练过程的变化。