相控阵天线——基于MATLAB对线阵进行道尔夫—切比雪夫加权
目录
前言
一、阵列天线的综合
二、道尔夫—切比雪夫综合
三、单元间距的改变对切比雪夫阵列方向图的影响
四、单元数的改变对切比雪夫阵列激励分布的影响
五、副瓣电平SLL对切比雪夫阵列激励幅度的影响
六、副瓣电平SLL对切比雪夫阵列方向图的影响
七、MATLAB代码
总结
前言
阵列天线的综合问题是其分析的逆问题,即在预先给定辐射特性(如方向图形状、主瓣宽度、副瓣电平、方向性系数等)的情况下,综合出阵列单元数、间距、激励幅度和相位。阵列天线的综合就是阵列天线的设计问题。本文介绍根据方向图的主瓣宽度和副瓣电平对相控阵线阵天线进行切比雪夫加权(综合),并通过MATLAB仿真分析切比雪夫加权方法的优缺点。
提示:以下是本篇文章正文内容,希望能帮助到各位,转载请附上链接。
一、阵列天线的综合
可把阵列天线的综合问题分为以下4类:
①根据给定方向图主瓣宽度、副瓣电平的要求进行综合,方向图的其他细节不苛求。这类综合方法最著名的是道尔夫-切比雪夫综合法、泰勒综合法等。
②要求获得指定方向图形状的综合。这类综合方法实际上是函数逼近问题。有傅里叶变换法、伍德沃德-劳森综合法、优化计算方法等。
③微扰法综合阵列。即对阵列间距、激励幅度进行微扰,以得到逼近要求的方向图。
④对阵列天线参数(如方向性系数)进行优化设计,及根据给定赋形方向图进行优化综合。
二、道尔夫—切比雪夫综合
这是一种可控制副瓣电平的阵列天线综合方法,也是工程实际中常用的综合方法之一,简称切比雪夫综合法。由这种综合方法设计的阵列称为切比雪夫阵列。切比雪夫阵列的特点是:
①其方向图为等副瓣。
②在相同副瓣电平和相同阵列长度下其方向图主瓣最窄,称为最佳阵列。
③ 单元数多,且副瓣电平要求不是很低时,阵列两端单元激励幅度跳变大。
在此之前我们分析的阵列天线,其副瓣电平均较高。为了使雷达系统具有较高的抗干扰、抗反辐射导弹等能力,往往要求雷达天线的副瓣尽量低。采用道尔夫-切比雪夫综合法、泰勒综合法等设计的阵列天线就可实现低副瓣。
阶数为0-5的切比雪夫函数的曲线如下图所示:

结合曲线图,可总结出切比雪夫多项式具有如下重要性质:

切比雪夫综合法的主要思想为:
从切比雪夫函数曲线看,道尔夫实现了利用(
为最靠近
的零点)区间内的
曲线作为方向图主瓣, 区间
内的
的振荡曲线作为方向图的等电平副瓣。而且适当地选择
还可以调整主瓣和副瓣的比值
。
对于道尔夫-切比雪夫加权可以直接通过求解切比雪夫多项式去综合,也可以直接使用MATLAB自带的函数去综合。这里我们使用MATLAB自带的函数去综合。
I=chebwin(N,SLL); %N为阵元数,SLL为副瓣电平,I包含各阵元的激励幅度
仿真参数设置为:
f=2e9; %频率,单位Hz
N=16; %阵元数
mu=1/2; %阵元间距÷波长
theta0=0;%波束指向角度,单位°
SLL=30; %副瓣电平,单位dB

三、单元间距的改变对切比雪夫阵列方向图的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
N=10; %阵元数
theta0=0;%波束指向角度,单位°
SLL=20; %副瓣电平,单位dB
依次设置,
,
,
,观察方向图及激励幅度分布。
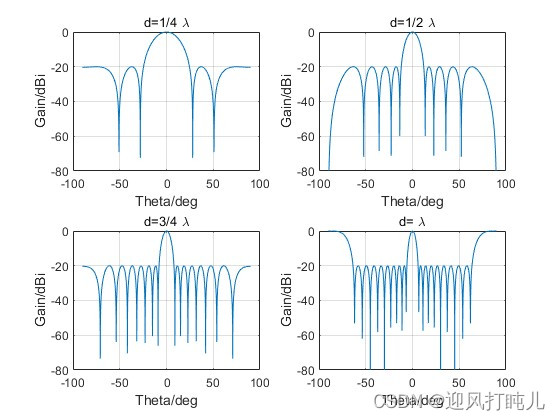

可知,随着阵元间距d的增大,切比雪夫阵列方向图的主瓣变窄,副瓣增多,但间距d的改变并不影响切比雪夫阵列的激励分布。切比雪夫阵列的激励分布与单元数,副瓣电平密切相关。
切比雪夫阵列激励幅度分布的通用综合公式由巴贝尔给出,称为巴贝尔公式。
偶数阵列():
奇数阵列():
其中,。
四、单元数的改变对切比雪夫阵列激励分布的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
theta0=0; %波束指向角度,单位°
mu=1/4; %阵元间距÷波长
当SLL=25dB时,依次设置N=15,20,25,30,35,观察激励幅度的分布;当SLL=35dB时,依次设置N=15,20,25,30,35,观察激励幅度的分布。
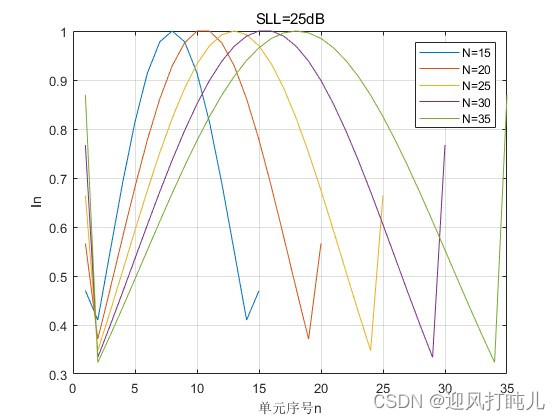
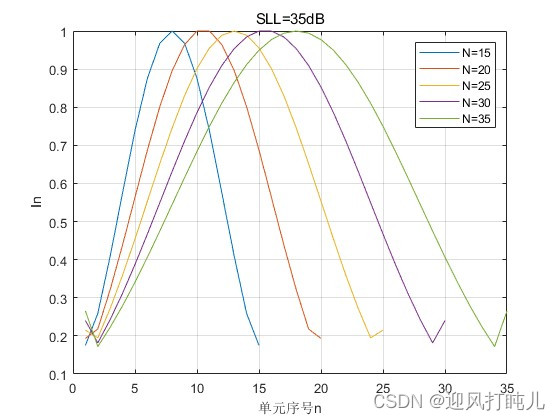
由以上两图可见,当单元数增多时,阵列两端单元的激励幅度跳变增大,副瓣电平越高,跳变幅度越大。这种幅度跳变大到一定程度时将给馈电网络的设计带来一定困难。
所以,对大型阵列来说一般不采用切比雪夫方法综合阵列,除非是低副瓣。需要说明的是,切比雪夫综合的只是激励幅度分布,激励相位为零。
五、副瓣电平SLL对切比雪夫阵列激励幅度的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
theta0=0;%波束指向角度,单位°
mu=1/2; %阵元间距÷波长
N=20; %阵元数
当N=20时,依次设置SLL=20,25,30,35,40dB,观察激励幅度的分布。
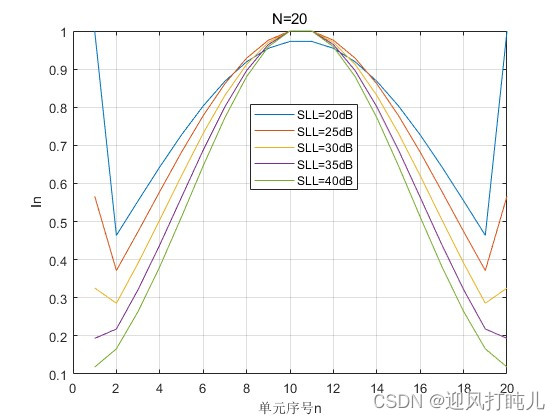
由此图可看出,副瓣电平越低,两端单元的激励幅度跳变越大。随着SLL的增大,两端单元的激励幅度跳变逐渐减小。
六、副瓣电平SLL对切比雪夫阵列方向图的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
N=16; %阵元数
theta0=20;%波束指向角度,单位°
mu=1/2; %阵元间距÷波长
依次设置SLL=10,20,30,40dB,观察方向图。

由上图可见,单元数N和间距d不变,随着方向图副瓣电平的降低,主瓣宽度将会增大。
七、MATLAB代码
https://download.csdn.net/download/m0_66360845/89481296![]() https://download.csdn.net/download/m0_66360845/89481296
https://download.csdn.net/download/m0_66360845/89481296
总结
以上就是今天要分享的全部内容,本文介绍了切比雪夫加权方法对线阵进行综合,同时也分析了间距、单元数,副瓣电平等参数对激励幅度以及方向图的影响。
