5. 买卖股票的最佳时机含冷冻期
309. 最佳买卖股票时机含冷冻期
算法原理
- 确定状态表示
dp[i]:表示第i天的最大利润
- 细分
- 第
i天结束的时候是“买入”状态(0) - 第
i天结束的时候是“可交易”状态(1) - 第
i天结束的时候是“冷冻期”状态(2)
- 第
- 状态转移方程
分析状态的时候,就一个状态一个状态的看(一共 3 x 3=9 种)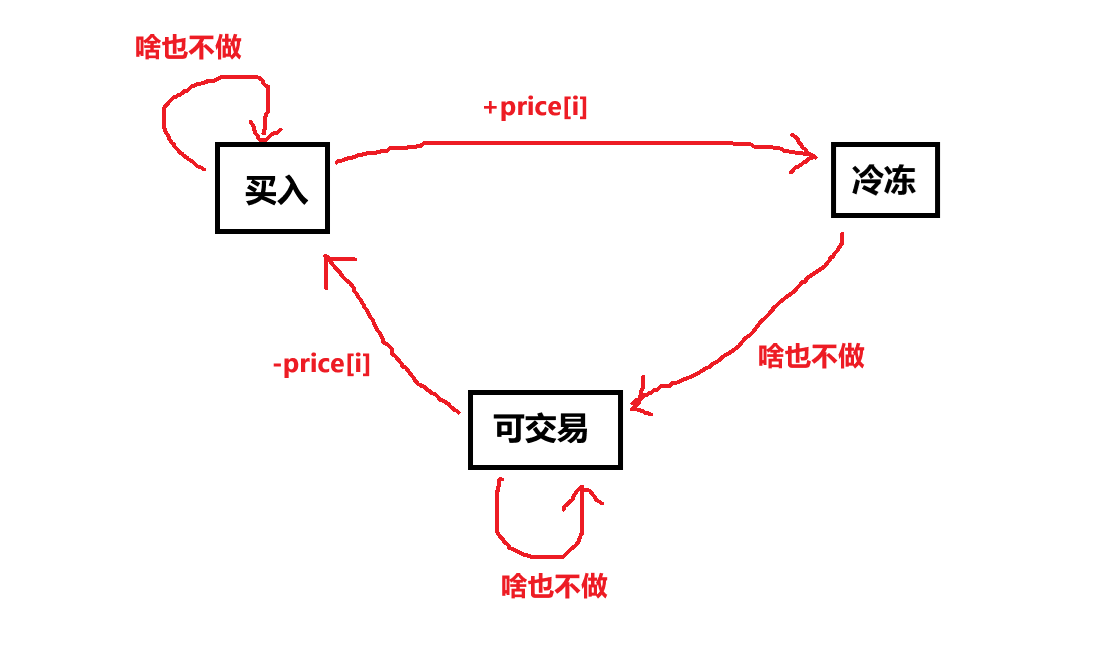
- 买入
-
“买入“==>“买入”;在
i-1天的时候什么也不干,到了第i天之后已然是“买入状态” -
“可交易”==>“买入”:在第
i天进行股票买入,-price[i] -
“冷冻期”x=>“买入”:这一天无法交易,故不能买入股票,所以无法实现
-
dp[i][0] = max(dp[i-1][0], dp[i-1][1] - price[i])
-
- 可交易
-
“可交易”==>“可交易”:i-1 天不买,则到了 i 天也是“可交易”
-
“冷冻期”==>“可交易”:i-1 天是冷冻期,则第 i 天就是可交易的了
-
“买入”x=>可交易:必须得经过冷冻期
-
dp[i][1] = max(dp[i-1][1], dp[i-1][2])
-
- 冷冻期
-
“冷冻期”x=>“冷冻期”:不能连续两天都是“冷冻期”
-
“买入”==>“冷冻期”:在第 i 天将股票给卖了,就变成“冷冻期”了,
+price[] -
“可交易”x=>“冷冻期”:到不了手里没股票,没卖的
-
dp[i][2] = dp[i-1][0] + price[i]
-
-
初始化
- 都出现了
i-1,所以要初始化第一个位置 dp[0][0] = -price[0]dp[0][1] = 0dp[0][2] = 0
- 都出现了
-
填表顺序
- 从左往右
- 一次填写三个表
-
返回值
- 返回
max(dp[n-1][1], dp[n-1][2]) - 第一个表肯定不是最终答案,手里的股票都还没卖,肯定比卖出去的低
- 返回
代码编写
public int maxProfit(int[] prices) { int n = prices.length; int[][] dp = new int[n][3]; //2. 初始化 dp[0][0] = -prices[0]; //3. 填表 for (int i = 1; i < n; i++) { dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]); dp[i][1] = Math.max(dp[i-1][1], dp[i-1][2]); dp[i][2] = dp[i-1][0] + prices[i]; } return Math.max(dp[n-1][1], dp[n-1][2]);
}
6. 买卖股票的最佳时期含手续费
714. 买卖股票的最佳时期含手续费
算法原理
-
确定状态表示
dp[i]表示:第 i 天结束之后,所能获得的最大利润f[i]:处于“买入”,有股票,此时的最大利润g[i]:处于“卖出”,可交易,此时的最大利润 `
-
状态转移方程

f[i] = max(f[i-1], g[i-1] - price[i])g[i] = max(g[i-1], f[i-1] + price[i] - fee)
-
初始化
- 第 0 天的时候处于买入状态,那就只能把那天的股票买了
f[0] = -price[0] - 第 0 天的时候处于卖出的状态,那就啥也不干
g[0] = 0
- 第 0 天的时候处于买入状态,那就只能把那天的股票买了
-
填表顺序
- 从左往右
- 两表一起填
-
返回值
- 只有处于卖出状态才可能是最大利润
- 直接返回
g[n-1]
代码编写
public int maxProfit(int[] prices, int fee) { int n = prices.length; int[] f = new int[n]; int[] g = new int[n]; f[0] = -prices[0]; for (int i = 1; i < n; i++) { f[i] = Math.max(f[i-1], g[i-1]-prices[i]); g[i] = Math.max(g[i-1], f[i-1]+prices[i]-fee); } return g[n-1];
}
7. 买卖股票的最佳时机 III
123. 买卖股票的最佳时机 III
算法原理
- 确定状态表示
dp[i]表示:第 i 天结束之后,所能获得的最大利润
一维表示第 i 天;二维表示交易次数(可加一维表示买入还是卖出,不过我们可以直接用两个表)
f[i][j]:第 i 天结束后,完成了 j 次交易,此时处于“买入“状态下的最大利润g[i][j]:第 i 天结束后,完成了 j 次交易,此时处于“卖出”状态下的最大利润
- 状态转移方程
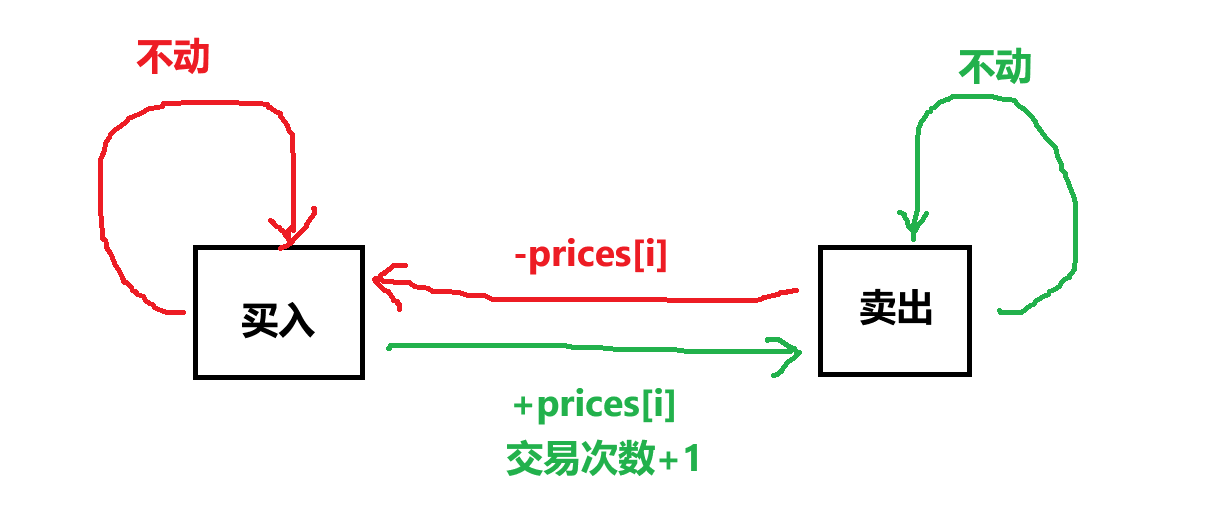
f[i][j] = max(f[i-1][j], g[i-1][j]-prices[i-1])g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i]),今天的交易次数是 j,要找到昨天的,就得j-1。g[i][j] = g[i-1][j]。因为第一次的时候,j-1<0,不符合要求if(j-1>=0) g[i][j] = max(g[i][j], f[i-1][j-1]+prices[i])
此处分析没有定义 j 的大小(交易次数),
- 初始化
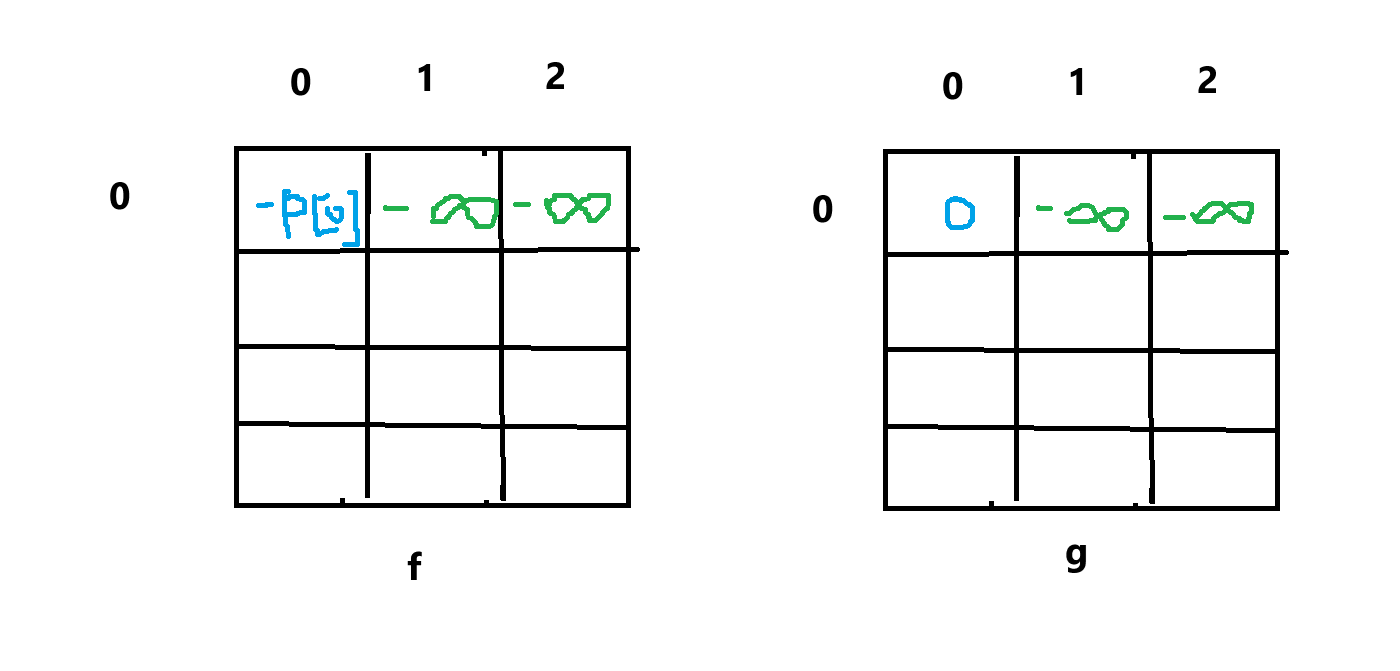
- 只需要初始化第一行。横坐标表示第 0 天结束之后,纵坐标表示完成交易笔数
- 选最小值的时候,不能选
INT_MIN,因为上面还有-1 的操作,会导致越界。所以我们取-0x3f3f3f3f,这是最小值的一半
-
填表顺序
- 从上往下填写每一行
- 每一行从左往右
- 两表一起填
-
返回值
g表的最后一行里面的最大值- 不考虑
f表,因为f表手里的股票都还没卖出去,肯定不会是最大利润
代码编写
public int maxProfit(int[] prices) { int n = prices.length; int[][] f = new int[n][3]; int[][] g = new int[n][3]; for (int i = 1; i < 3; i++) { f[0][i] = -0x3f3f3f3f; g[0][i] = -0x3f3f3f3f; } f[0][0] = -prices[0]; for (int i = 1; i < n; i++) { for (int j = 0; j < 3; j++) { f[i][j] = Math.max(f[i-1][j], g[i-1][j]-prices[i]); g[i][j] = g[i-1][j]; if(j-1 >= 0) g[i][j] = Math.max(g[i][j], f[i-1][j-1]+prices[i]); } } int ret = 0; for (int i = 0; i < 3; i++) { ret = Math.max(ret, g[n-1][i]); } return ret;
}
8. 买卖股票的最佳时机 Ⅳ
188. 买卖股票的最佳时机 Ⅳ
算法原理
和上一题一样,只是把 2 变成了 k
代码编写
public int maxProfit(int k, int[] prices) { int n = prices.length; int MIN = -0x3f3f3f3f; int[][] f = new int[n][k+1]; int[][] g = new int[n][k+1]; for (int i = 0; i <= k; i++) { f[0][i] = MIN; g[0][i] = MIN; } f[0][0] = -prices[0]; g[0][0] = 0; for (int i = 1; i < n; i++) { for (int j = 0; j < k+1; j++) { f[i][j] = Math.max(f[i-1][j], g[i-1][j]-prices[i]); g[i][j] = g[i-1][j]; if(j-1 >= 0) g[i][j] = Math.max(g[i-1][j], f[i-1][j-1]+prices[i]); } } int ret = 0; for (int i = 0; i < k+1; i++) { ret = Math.max(ret, g[n-1][i]); } return ret;
}




