一、映射
1.1 映射的概念
存在一个法则 f ,使得对 X 中每个元素 x ,在 Y 中有唯一确定的元素 y 与之对应(X、Y 非空集)
称 f 为从 X 到 Y 的映射,如图所示

其中 y 称为元素 x(在映射 f 下)的像,并记作 x ,如图所示
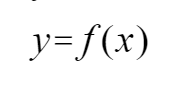
而元素 x 称为元素 y (在映射 f 下)的一个原像
集合 X 称为映射 f 的定义域,记作
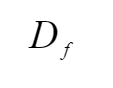
X 中所有元素的像所组成的集合称为映射 f 的值域,记作
引用书上的案例,给出法则 f,可得出定义域和值域
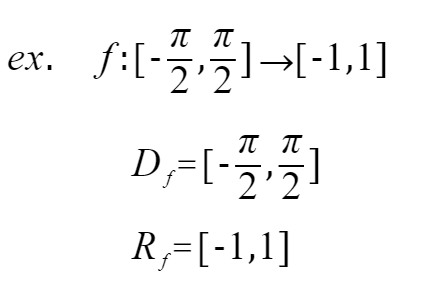
Y 中任一元素 y 都是 X 中某元素的像时称 f 为 X 到 Y 上的映射或满射
如果对于 X 中的任意两个不同的元素 x1 和 x2,当 x1≠x2 时,总有 f(x1)≠f(x2),则 f 为 X 到 Y 的单射,如图所示
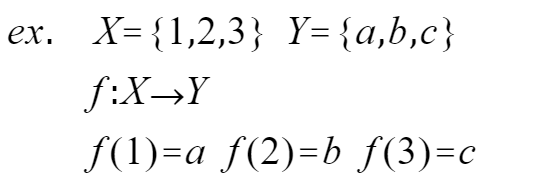
若既是单射又是满射则称为双射(上面第一个案例即是)

1.2 逆映射与复合映射
接上述,f 是 X 到 Y 的映射,可定义新的映射
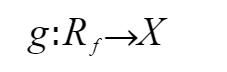
规定 g(y)=x,x 满足 f(x)=y 时,称 g 为 f 的逆映射,记作
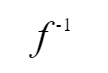
其定义域和值域分别为:
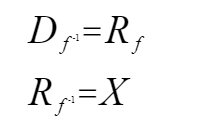
注意:只有单射才满足逆映射
现在假设有两个映射

其中 Y2 包含 Y1,那么可以得出一个 X 到 Z 对应法则,这个映射由 g 和 f 构成,称为复合映射
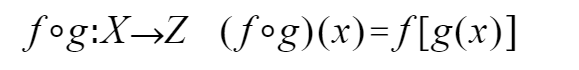
二、函数
2.1 函数的特性
2.1.1 有界性
一个函数 f: X ➡ Y 的有界性可以分为以下几种情况:

函数的有界性是函数的一个重要特性,具体体现在以下几点:
- 上有界:函数值不超过某个最大值。
- 下有界:函数值不低于某个最小值。
- 有界:函数值在某个上下限之间。

2.1.2 单调性
单调递增
函数 f: X ➡ Y 在定义域 X 上是单调递增的,如果对于任意的 x1,x2 ∈ X,当 x1 < x2 时,总有 f(x1) ≤ f(x2)
单调递减
函数 f: X ➡ Y 在定义域 X 上是单调递减的,如果对于任意的 x1,x2 ∈ X,当 x1 < x2 时,总有 f(x1) ≥ f(x2)

2.1.3 奇偶性
偶函数:关于 Y 轴对称,即 f(x) = f(-x)
奇函数:关于原点对称,即 f(-x) = -f(x)

2.1.4 周期性
它描述了函数在某一固定间隔内重复其值的性质
一个函数 f 被称为周期函数,如果存在一个非零常数 T 使得对于定义域中的每一个 x,都有:
f(x+T) = f(x)
这个非零常数 T 被称为函数 f 的周期(通常是最小周期)

2.2 反函数与复合函数
2.2.1 反函数
用之前的逆映射的案例,f-1 为函数 f 反函数,原来的函数称为 直接函数
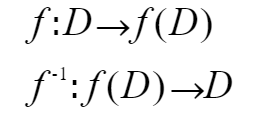

反函数的性质:

2.2.2 复合函数
定义:


复合函数的性质:

2.3 函数的运算

