ChatGPT+数学建模：快速搞定2024国赛A题“板凳龙”！

ChatGPT+数学建模：快速搞定2024国赛A题“板凳龙”！

2024数学建模国赛A题“板凳龙”详细思路

数学建模GPT使用网站：

https://new.chatgpt-plus.top/list/

问题分析

题目要求参赛者为板凳龙的运动建立数学模型，并解决若干相关问题。具体涉及螺线运动、板凳之间的刚性约束、碰撞检测、调头空间优化等。为了更好地处理这些问题，我们将采用空间几何和运动学模型来描述板凳龙的运动状态，并结合MATLAB进行数值求解。

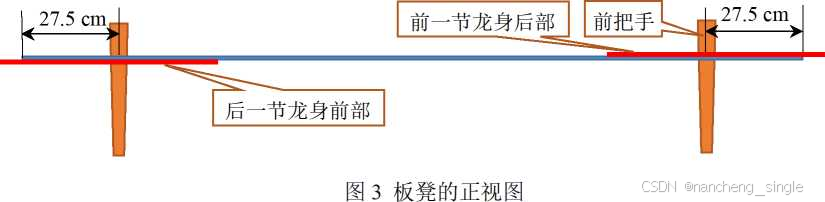
问题一：舞龙队沿螺距为55 cm的等距螺线顺时针盘入

1. 思路分析

此问题要求计算舞龙队沿螺线的运动轨迹，龙头速度为1 m/s。我们需要从初始时刻开始，每秒计算龙头、龙身和龙尾各把手的准确位置和速度。整个运动是一个螺旋运动，可以利用螺线的几何特性来描述运动轨迹。

几何建模：通过螺线参数方程计算出每个时刻的龙头位置，并通过龙头的运动递推计算龙身和龙尾的位置。

2. 空间螺线运动学模型

采用极坐标系来表示螺线运动。螺线的参数方程如下：

• ( r = a \theta )
• 将极坐标转换为笛卡尔坐标：

  • ( x = a \theta \cos(\theta) )
  • ( y = a \theta \sin(\theta) )

其中，( a ) 是螺线的参数，由螺距 ( p ) 和 ( \theta ) 相关。通过龙头的恒定速度，可以推导出龙头在不同时刻的位置。

3. MATLAB 代码实现

% 定义常量
L_head = 3.41; % 龙头长度（米）
L_body = 2.20; % 龙身长度（米）
spiral_pitch = 0.55; % 螺距（米）
a = spiral_pitch / (2 * pi); % 螺线参数
v_head = 1; % 龙头速度（米/秒）
total_time = 300; % 总时间（秒）
dt = 1; % 时间步长（秒）
n_segments = 223; % 板凳总数

% 初始化数组
t = 0:dt:total_time;
theta = zeros(size(t));
x = zeros(n_segments, length(t));
y = zeros(n_segments, length(t));
vx = zeros(n_segments, length(t));
vy = zeros(n_segments, length(t));

% 计算初始theta（第16圈）
theta(1) = 16 * 2 * pi;

% 主循环
for i = 2:length(t)
    % 计算新的theta
    theta(i) = theta(i-1) + v_head * dt / a; 

    % 计算龙头位置
    x(1,i) = a * theta(i) * cos(theta(i));
    y(1,i) = a * theta(i) * sin(theta(i));
    
    % 计算龙身和龙尾位置和速度
    for j = 2:n_segments
        % 计算新位置和速度
        % 此处根据每节板凳的长度，递推计算其他板凳的位置
        delta_theta = (L_body / a) / sqrt(1 + (theta(i) - theta(i-1))^2);
        x(j,i) = x(j-1,i) + L_body * cos(delta_theta);
        y(j,i) = y(j-1,i) + L_body * sin(delta_theta);
        
        % 计算速度
        vx(j,i) = (x(j,i) - x(j,i-1)) / dt;
        vy(j,i) = (y(j,i) - y(j,i-1)) / dt;
    end
end

% 保存结果到Excel文件
result = zeros(n_segments * 2, length(t));
for i = 1:n_segments
    result(2*i-1, :) = x(i, :);
    result(2*i, :) = y(i, :);
end
writematrix(result', '问题1_result1.xlsx');

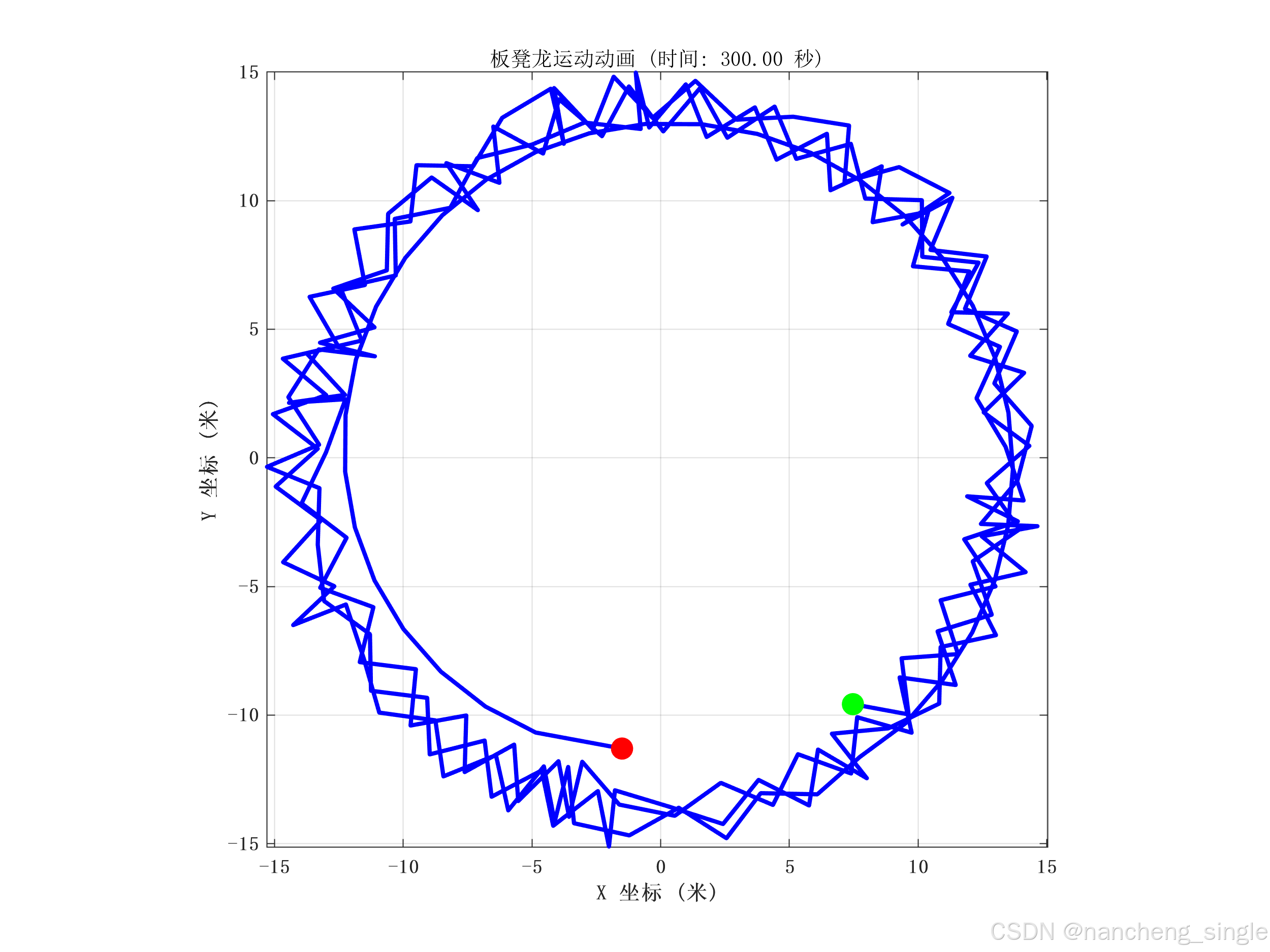
% 绘制运动轨迹图
figure('Position', [100, 100, 800, 600]);
plot(x(1,:), y(1,:), 'r-', 'LineWidth', 2);
hold on;
plot(x(end,:), y(end,:), 'b-', 'LineWidth', 2);
plot(x(:,end), y(:,end), 'g-', 'LineWidth', 2);
title('板凳龙运动轨迹');
xlabel('X 坐标 (米)');
ylabel('Y 坐标 (米)');
legend('龙头轨迹', '龙尾轨迹', '最终位置');
grid on;

4. 模型分析与总结

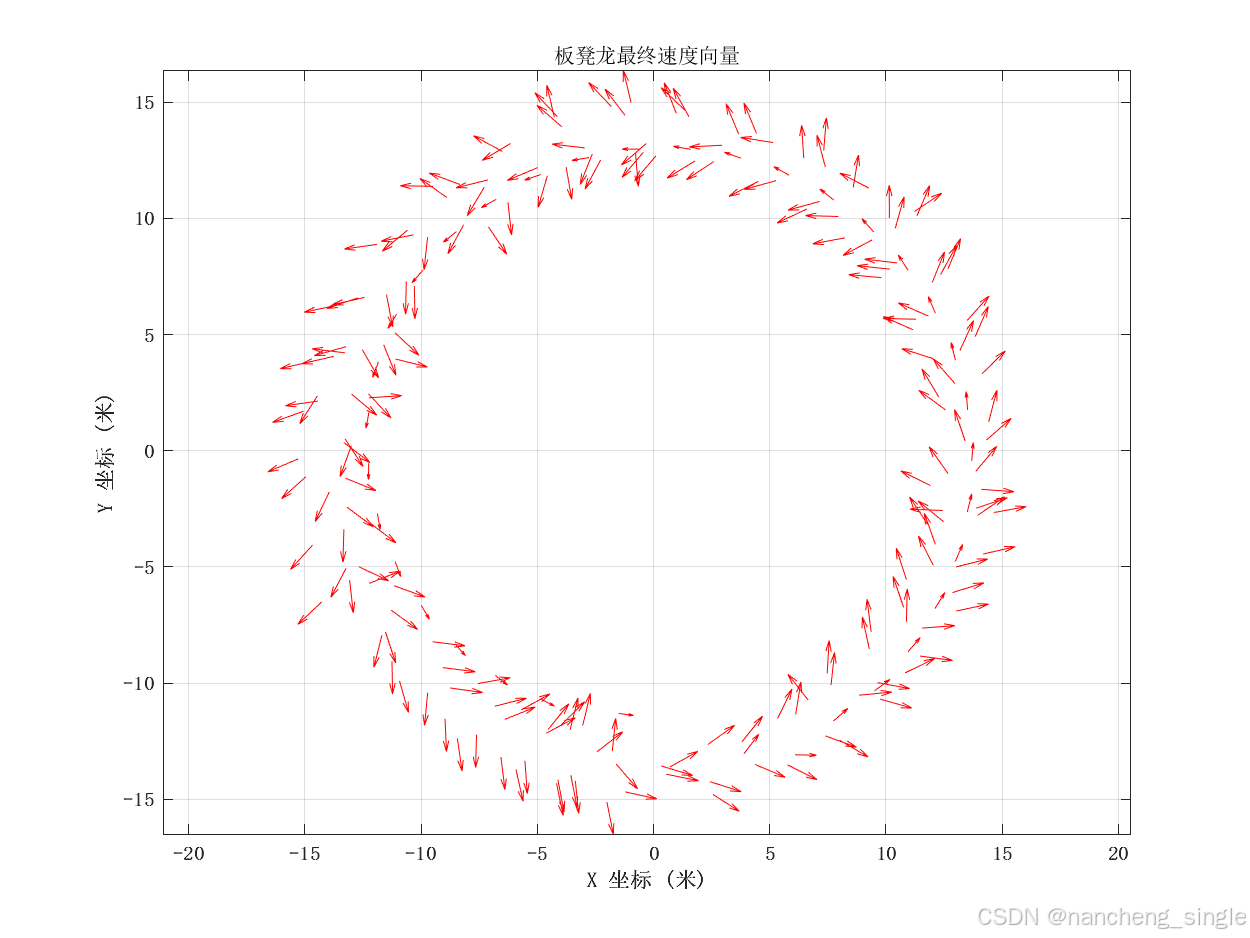
该模型通过递推计算龙头、龙身和龙尾在螺线上的位置及其速度，结果保存在Excel文件中供进一步分析。通过MATLAB的数值计算，可以高效地处理大量数据点，并生成运动轨迹图来可视化整个过程。

问题二：确定舞龙队盘入的终止时刻

1. 碰撞检测模型

为确保板凳之间不发生碰撞，我们需要建立碰撞检测的几何模型。检测条件可通过判断板凳间的最小距离来实现，结合MATLAB中的迭代方法，可以精确找到舞龙队盘入的终止时刻。

问题三和四：调头空间和路径优化

这两个问题涉及螺距和调头路径的优化问题，需根据龙头前把手的运动情况，优化螺距和路径。可通过非线性优化模型求解，使用MATLAB的优化工具箱来完成。

插图参考

数学建模GPT使用网站：

https://new.chatgpt-plus.top/list/