黄页软件app开发_网站制作文章标签_开发定制软件公司_seoul是哪个国家

目录

一、希尔排序定义

二、希尔排序原理

三、希尔排序特点

四、两种解法

五、代码实现

---

一、希尔排序定义

希尔排序是一种基于插入排序的排序算法，也被称为缩小增量排序。它通过将待排序的数组分割成若干个子序列，对子序列进行排序，然后逐步合并这些子序列，最终得到一个有序的数组。希尔排序的特点是可以通过设置不同的增量序列来改变算法的效率，通常选择的增量序列是经过优化的递减数列。希尔排序的时间复杂度取决于增量序列的选择，通常为O(n log n)到O(n^2)之间。这种排序算法由Donald Shell于1959年提出并命名。

二、希尔排序原理

希尔排序是一种插入排序的改进算法，也称为缩小增量排序。其原理是先将待排序的元素分成若干个子序列，对各个子序列进行插入排序，然后逐步缩小增量，重复上述操作，直到增量为1，最终对整个序列进行插入排序。

具体步骤如下：

1. 选择一个增量序列，通常取增量序列的最后一个元素为1，对序列进行分组，每组的间隔为增量。
2. 对每组进行插入排序。
3. 缩小增量，重复第2步，直到增量为1。
4. 最后进行一次插入排序，完成排序过程。

希尔排序的优点是在每一轮排序中，距离较远的元素可以进行比较和交换，从而更快地将大的元素移动到合适的位置。这种子序列的插入排序思想使得希尔排序比普通的插入排序效率更高。

增量为5： 

增量为3：

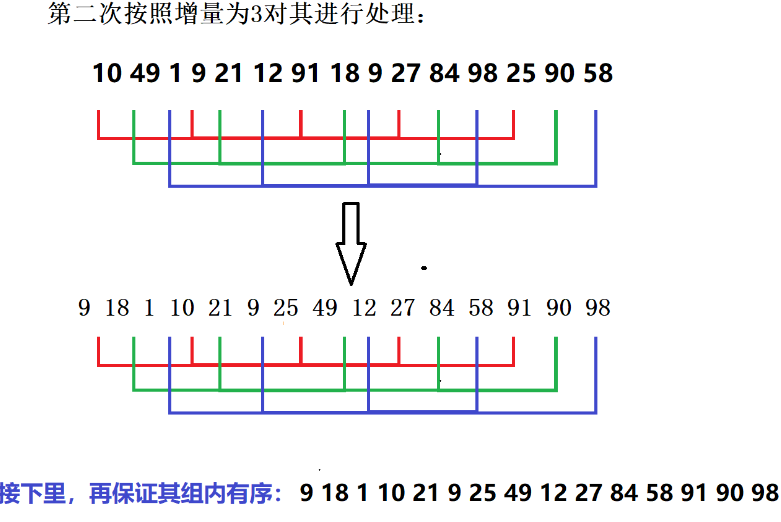
增量为1：

三、希尔排序特点

希尔排序是一种插入排序的改进版，其特点包括：

1. 非稳定排序：希尔排序是一种非稳定排序算法，即在排序过程中可能改变相同元素的相对位置。

2. 不同步距离的排序：希尔排序通过设定不同的间隔序列（称为增量序列）来对数据进行排序，不同的增量序列会影响排序的效率。

3. 时间复杂度：希尔排序的平均时间复杂度为O(n log n)到O(n^2)，取决于选择的增量序列。

4. 空间复杂度：希尔排序是原地排序算法，空间复杂度为O(1)。

5. 适用性：希尔排序适用于中等大小的数据集合，对于大规模数据集合的性能可能不如快速排序等算法。

6. 对于大规模数据集合的性能可能不如快速排序等算法。

7. 稳定性：不稳定

四、两种解法

第一种解法：每一个组都单独调用直接插入排序，这时需要3次执行插入排序的调用。

第二种解法：每一个组是隔离的，但是我们将其假象到同一个组内。

这时，处理值的顺序：红2，绿2，蓝2，红3，绿3，蓝3，红4，绿4，蓝4，红5，绿5，蓝5。

五、代码实现

void Shell(int arr[], int len, int gap)
{//第一种解法：每一组都单独插入排序//第二种解法：每个组是隔离的，但是将其假想到同一个组内int i, j;for (i = gap; i < len; i++){int tmp = arr[i];//i下标的值就是我们这一趟准备插入的值for (j = i - gap; j >= 0; j -= gap)//j下标一开始保存已排序好的序列的最右端值的下标，逐步向左走{if (arr[j] > tmp){arr[j + gap] = arr[j];}else{//插入情况1：  找到了一个 <= 准备插入的值break;}}//如果代码执行到这，代表着触底。//插入情况2：已排序好的序列中的值都比tmp的值大arr[j + gap] = tmp;}
}void Shell_Sort(int arr[], int len)
{//增量数组int gap[] = { 5,3,1 };for (int i = 0; i < sizeof(gap) / sizeof(gap[0]); i++){//每一趟单独执行希尔排序(需要告诉我们这一趟按哪个增量处理)Shell(arr, len, gap[i]);}
}void Show(int arr[], int len)
{for (int i = 0; i < len; i++){printf("%d ", arr[i]);}printf("\n");
}

测试用例代码：

int main()
{int arr[] = { 2,4,3,1,6,5,7,9,10,8 };int len = sizeof(arr) / sizeof(int);Shell_Sort(arr, len);Show(arr, len);return 0;
}

运行结果如下：