精准客户信息一条多少钱_网站搭建东莞_谷歌google play官网_如何做推广推广技巧

一、双指针

1、双指针算法概述

2、对撞指针

简介

求解步骤

例题

3、快慢指针

简介

求解步骤

例题

4、总结

二、快速排序

1、快速排序的思想

2、快速排序的实现

3、快速排序的实现（Partition函数）

4、快速排序的实现（图示）

5、例题讲解（蓝桥云课）

三、模拟

一、模拟算法介绍

1. 模拟算法概述

2. 模拟算法的风格

3. 例题(蓝桥oj五四九扫雷)

1）题目解析

二、例题

1）题目描述

2）题目解析

3）代码实现

3. 例题

1）题目描述

2）解题思路

3）关键点与细节

4）题目解析

4. 例题

1）回文日期

2）题目解析

3）代码实现与测试

4）总结

三、知识小结

四、二分法

1. 二分法简介

1）二分法定义与性质

2）二分法解题步骤

2. 解题步骤

1）整数二分

3）浮点二分

4）二分答案

二、知识小结

五、贪心

一、贪心算法介绍

1. 学习目标

2. 贪心的基本原理

3. 贪心的局限性

4. 贪心的特征

5. 贪心的类型

二、贪心算法实现步骤

1. 确定问题的最优子结构

2. 构建贪心选择的策略

3. 通过贪心选择逐步求解问题

4. 例题

1）题目解析

三、常见贪心模型和例题

1. 例题

1）题目描述

2）解题思路

3）代码实现

4）题目解析

5）总结

2. 例题

1）题目背景

2）贪心策略

3）实现方法

4）题型(蓝桥OJ545谈判)

3. 例题

1）题目背景

2）题目要求

3）解题思路

4）题目解析

4. 例题

1）题目背景

2）解题思路

3）题型(蓝桥云课分糖果问题)

4）实现细节

四、知识小结

一、双指针

1、双指针算法概述

定义：双指针算法是一种常用的算法技巧，通常用于在数组或字符串中进行快速查找、匹配、排序或移动操作。
实现：双指针并非真的用指针实现，一般用两个变量来表示下标。
应用场景：双指针算法使用两个指针在数据结构上进行迭代，并根据问题的要求移动这些指针。双指针往往与单调性、排序联系在一起，可以优化时间复杂度从O(n^2)到O(n)。
常见模型：
- 对撞指针
- 快慢指针

2、对撞指针

简介

定义：两个指针left和right分别指向序列的第一个元素和最后一个元素。然后left指针不断递增，right指针不断递减，直到两个指针相撞或错开，或者满足其他特殊条件。
应用场景：对撞指针一般用来解决有序数组或者字符串问题（常见于区间问题）：
- 查找有序数组中满足某些约束条件的一组元素问题：比如二分查找、数字之和等问题。
- 字符串反转问题：反转字符串、回文数、颠倒二进制等问题。

求解步骤

使用两个指针left和right：left指向序列第一个元素，right指向序列最后一个元素。
在循环体中将左右指针相向移动：①当满足一定条件时，将左指针右移，left++；②当满足另外一定条件时，将右指针左移，right--。
直到两指针相撞（即left == right），或者满足其他特殊条件时，跳出循环体。

例题

#include<bits/stdc++.h>
using namespace std;
const int N=10e6+9;
char s[N];int main(){cin>>s+1;int n=strlen(s+1);int l=1,r=n;bool ans=true;while(l<r &&ans){if(s[l]!=s[r]) ans=false;l++;r--;}cout<<(ans?"Y":"N")<<endl;return 0;
}

3、快慢指针

简介

定义：两个指针从同一侧开始遍历序列，且移动的步长一个快一个慢。移动快的指针称为快指针，移动慢的指针称为慢指针。
应用场景：快慢指针一般比对撞指针更难想，也更难写。常用于解决需要维护区间的问题。

求解步骤

使用两个指针l和r：l一般指向序列第一个元素，r一般指向序列第零个元素，初始时区间[l, r]为空。
在循环体中将左右指针向右移动：①当满足一定条件时，将慢指针右移，l++；②当满足另外一定条件时，将快指针右移，r++，保持[l, r]为合法区间。
直到快指针移动到数组尾端，或者两指针相交，或者满足其他特殊条件时跳出循环体。

例题

EX1:

#include<bits/stdc++.h>
using namespace std;int main(){long long n;cin>>n>>s;long long a[n+1];for(long long i=1;i<=n;i++)cin>>a[i];long long ans=n+1;for(long long i=1,j=0,sum=0;i<=n;++i){//考虑移动j，即j++ while(i>j || (j+1<=n && sum<s))sum+=a[++j];if(sum>=s)ans=min(ans,j-i+1);sum-=a[i];}cout<<(ans>n?0:ans)<<endl;return 0;
}

滑动窗口算法：
- 外层循环：for(long long i=1; i<=n; ++i)：遍历序列的每个元素作为窗口的左端点。
- 内层循环：while(i > j || (j+1 <=n && sum < s)) sum += a[++j];：扩展右指针j，直到窗口的和sum大于等于s或者j达到序列末尾。
- 更新答案：if(sum >= s) ans = min(ans, j - i +1);：如果当前窗口的和满足条件，更新最短长度。
- 收缩窗口：sum -= a[i];：当左指针i向右移动时，从sum中减去左指针指向的元素。

算法逻辑

滑动窗口技术：通过维护一个窗口[i, j]，动态调整窗口的大小，寻找满足条件的最短子数组。
单调性优化：利用窗口的单调性，确保每个元素只被访问一次，从而将时间复杂度从O(n^2)优化到O(n)。

代码关键点

滑动窗口的扩展和收缩：通过j++扩展窗口，通过i++收缩窗口。
条件判断：确保窗口的和大于等于s时，更新最短长度。
边界处理：处理窗口超出序列边界的情况。

EX2:

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+9;
long long a[N],s;int main(){int n,m,k;cin>>n>>m>>k;for(int i=1;i<=n;++i)cin>>a[i];int ans=0;for(int i=1,j=0,cnt=0 ;i<=n;++i){while(i>j ||(j+1<=n &&cnt<k))if(a[++j]>=m)cnt+=1;if(cnt>=k)ans+=n-j+1;if(a[i]>=m)cnt-=1;//如果a[i]是>=m那么cnt减去a[i] } cout<<ans<<endl;return 0;
}

滑动窗口算法：
- 外层循环：for(int i=1; i<=n; ++i)：遍历序列的每个元素作为窗口的左端点。
- 内层循环：while(i > j || (j+1 <=n && cnt <k)) if(a[++j]>=m)cnt+=1;：扩展右指针j，直到窗口中满足条件的元素数量达到k或者j达到序列末尾。
- 更新答案：if(cnt >=k) ans += n -j +1;：如果当前窗口满足条件，更新答案计数器。
- 收缩窗口：if(a[i]>=m)cnt-=1：当左指针i向右移动时，从cnt中减去左指针指向的元素是否满足条件。

算法逻辑

滑动窗口技术：通过维护一个窗口[i, j]，动态调整窗口的大小，寻找满足条件的子串。
单调性优化：利用窗口的单调性，确保每个元素只被访问一次，从而将时间复杂度从O(n^2)优化到O(n)。

代码关键点

滑动窗口的扩展和收缩：通过j++扩展窗口，通过i++收缩窗口。
条件判断：确保窗口中满足条件的元素数量达到k时，更新答案计数器。
边界处理：处理窗口超出序列边界的情况。

4、总结

双指针算法是一种高效的算法技巧，适用于数组和字符串的多种问题。
对撞指针适用于需要从两端向中间遍历的问题，如回文检查。
快慢指针适用于需要维护区间的问题，如寻找满足条件的最短子数组。

二、快速排序

1、快速排序的思想

快速排序是一种基于分治法的排序方法，原理是将一个数组分成两个子数组，其中一个子数组的所有元素都小于另一个子数组的元素，然后递归地对这两个子数组进行排序。
快速排序的思想是通过不断地将数组分成两个子数组，递归地对子数组进行排序，最终得到一个有序的数组。这个过程通过选择合适的基准和分区操作来实现。
快速排序拥有更好的时间复杂度O(nlogn)，且不需要额外空间。

2、快速排序的实现

void QuickSort(int a[], int l, int r)
{if(l < r){int mid = Partition(a, l, r);QuickSort(a, l, mid - 1);QuickSort(a, mid + 1, r);}
}

说明：这是快速排序的递归主体QuickSort()。传入参数为要排序的数组和区间的左右端点。
Partition函数会将数组a[l] ~ a[r]这个区间中某个基准数字放到正确的位置并将这个位置返回。
在确定了mid的位置之后，可以保证a[l] ~ a[mid - 1]都 < a[mid] < a[mid + 1] ~ a[r]，于是只需要将左右两边分别向下递归地排序即可。

3、快速排序的实现（Partition函数）

int Partition(int a[], int l, int r)
{int pivot = a[r];int i = l, j = r;while(i < j){while(i < j && a[i] <= pivot) i ++;while(i < j && a[j] >= pivot) j --;if(i < j) swap(a[i], a[j]);}swap(a[i], a[r]);return i;
}

说明：这是Partition函数（分区函数），用于将比pivot小的放到左边，大的放到右边，最后返回pivot所处的位置。
这个函数是本节课程的重中之重。

4、快速排序的实现（图示）

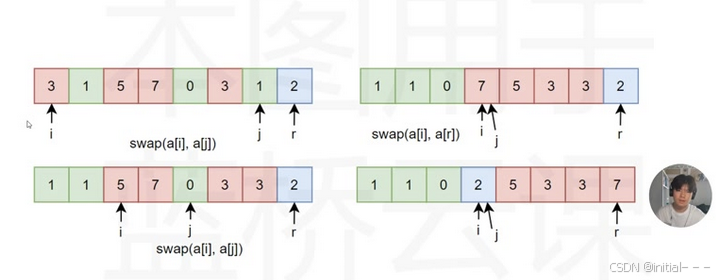
图示展示了Partition函数的执行过程，通过交换元素将数组分为两部分，一部分小于基准值，一部分大于基准值。

5、例题讲解（蓝桥云课）

题目描述：在一个神秘的岛屿上，有一支探险队发现了一些宝藏。这些宝藏是以整数数组的形式存在的。每个宝藏上都有一个数字，代表了其珍贵程度。然而，由于某种神奇的力量，这批宝藏的顺序被打乱了。探险队需要将宝藏按照珍贵程度进行排序，以便更好地研究和保护它们。作为探险队的一员，你需要设计合适的排序算法来将宝藏按照珍贵程度进行从小到大排序。
输入描述：
- 输入第一行包括一个数字n，表示宝藏总共有n个。
- 输入的第二行包括n个数字，第i个数字a[i]表示第i个宝藏的珍贵程度。
输出描述：输出n个数字，为对宝藏按照珍贵程度从小到大排序后的数组。
示例输入：

```
5
1 5 3 2 4
```
示例输出：
1 2 3 4 5
说明：用快速排序解决，前面讲过的几种排序方法的时间复杂度都是O(n^2)，所以只能解决规模在1e3左右的问题，快速排序拥有较好的时间复杂度O(nlogn)，所以可以解决更大规模的问题（约1e5）。

三、模拟

一、模拟算法介绍

1. 模拟算法概述

定义: 模拟算法通过模拟实际情况来解决问题，一般容易理解。
特点:
- 实现起来比较复杂，有很多需要注意的细节。
- 不涉及太难的算法，由较多简单但不好处理的部分组成。
- 考察选手的细心程度和整体的逻辑思维。
技巧: 为了使得模拟题逻辑清晰，经常会写较多的小函数来帮助解题，例如int和string的相互转换、回文串的判断、日期的转换、各种特殊条件的判断等。

2. 模拟算法的风格

暴力求解: 模拟算法往往写得比较暴力，不会卡时间复杂度，主要考察细腻程度。

3. 例题(蓝桥oj五四九扫雷)

1）题目解析

(具体解析内容根据课堂讲解进行补充，包括审题过程、解题思路、答案等)

二、例题

1）题目描述

题目内容: 在一个n行m列的方格图上有一些位置有地雷，另外一些位置为空。请为每个空位置标一个整数，表示周围八个相邻的方格中有多少个地雷。
输入格式: 第一行包含两个整数n和m，表示方格图的行数和列数。接下来n行，每行m个整数，0表示没有地雷，1表示有地雷。
输出格式: 输出n行，每行m个整数，表示每个空位置周围的地雷数量。如果某个位置是地雷，则输出9。

2）题目解析

解题思路
- 遍历每个位置: 使用两层循环遍历方格图上的每个位置。
- 特判地雷位置: 如果当前位置是地雷（值为1），则在答案矩阵中对应位置填9，并跳过该位置的后续处理。
- 扫描九宫格: 对于非地雷位置，扫描其周围八个相邻位置（即九宫格），统计地雷数量，并将结果填入答案矩阵。
- 输出答案: 最后输出答案矩阵。
注意事项
- 边界处理: 在扫描九宫格时，需要注意边界位置，避免越界访问。可以通过比较索引与边界值来确保不越界。
- 效率问题: 由于题目中给出的n和m的范围较大（最大为100），因此需要确保算法的效率。本题的解法时间复杂度为O(n*m)，在给定范围内是可接受的。
举例
- 示例输入:
- 示例输出:
- 解释: 对于示例输入中的每个空位置，我们计算其周围八个相邻位置中的地雷数量，并填入答案矩阵。例如，第一行第二个位置是地雷，所以答案矩阵中对应位置填9；第一行第一个位置周围只有一个地雷（在其右侧），所以答案矩阵中对应位置填1。以此类推，得到最终答案。

3）代码实现

##### 2. <iostream>
using namespace std;
int main() {int n, m;cin >> n >> m;int mp[105][105]; // 存储地图的二维数组，多开一些空间以避免边界问题int ans[105][105]; // 存储答案的二维数组// 输入地图for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {cin >> mp[i][j];}}// 遍历每个位置，计算地雷数量for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {if (mp[i][j] == 1) {ans[i][j] = 9; // 地雷位置填9} else {int count = 0;// 扫描九宫格，统计地雷数量for (int dx = -1; dx <= 1; ++dx) {for (int dy = -1; dy <= 1; ++dy) {int nx = i + dx, ny = j + dy;if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && mp[nx][ny] == 1) {++count;}}}ans[i][j] = count; // 将地雷数量填入答案矩阵}}}// 输出答案for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {cout << ans[i][j] << " ";}cout << endl;}return 0;
}

代码说明: 代码首先输入地图的尺寸n和m，然后使用一个二维数组mp来存储地图信息。接下来，使用另一个二维数组ans来存储答案。通过两层循环遍历地图上的每个位置，根据当前位置是否是地雷来更新答案数组。最后，输出答案数组即可。

3. 例题

1）题目描述

题目背景: 小蓝负责花园的灌溉工作，花园是一个n行m列的方格图形，其中一部分位置安装有出水管。
灌溉规则:
- 初始时，有出水管的位置被视为已灌溉。
- 每过一分钟，水会向四面扩展一个方格，被扩展到的方格被视为已灌溉。
输入:
- 花园的尺寸n和m。
- 出水管的位置，以(r, c)的形式给出。
- 经过的时间k分钟。
输出: k分钟后，有多少个方格被灌溉。

2）解题思路

数据表示:
- 使用两个二维布尔数组a和b，表示当前和后一分钟的灌溉情况。
- a[i][j] = 1表示第i行第j列的方格已被灌溉。
初始化:
- 根据出水管的位置，初始化数组a。
模拟灌溉过程:
- 使用循环，每次根据数组a更新数组b。
- 如果a[i][j] = 1，则b[i-1][j], b[i+1][j], b[i][j-1], b[i][j+1]都被设为1。
- 注意边界条件，确保索引不越界。
更新灌溉状态:
- 将数组b复制回数组a，为下一分钟的灌溉做准备。
计算结果:
- 循环k次后，扫描数组a，统计被灌溉的方格数量。

3）关键点与细节

布尔数组的使用:
- 使用布尔数组而不是整型数组，可以节省空间并简化判断逻辑。
双数组更新:
- 使用两个数组a和b分别表示当前和后一分钟的灌溉情况，避免在同一数组上操作导致的混乱。
边界处理:
- 在更新数组b时，不需要判断索引是否越界，因为即使越界，也不会影响最终结果。
时间复杂度:
- 每分钟需要扫描整个花园一次，时间复杂度为O(nmk)。

4）题目解析

审题: 明确题目要求，理解灌溉规则和输入输出格式。
初始化: 根据出水管位置初始化布尔数组a。
模拟灌溉: 使用循环和数组a、b模拟灌溉过程。
统计结果: 循环结束后，扫描数组a统计被灌溉的方格数量。
易错点:
- 忘记将当前已被灌溉的方格（即a[i][j] = 1的位置）在b数组中也设为1。
- 边界处理不当，导致数组越界或遗漏边界方格。
答案: 输出统计得到的被灌溉方格数量。
提交结果: 代码通过测试，得到正确答案。

4. 例题

1）回文日期

回文日期定义: 将日期按“yyyymmdd”格式写成一个8位数，如果这个数字是回文数，则称该日期为回文日期。例如，2020年2月2日（20200202）是一个回文日期。
特殊回文日期: 20200202不仅是一个回文日期，还是一个ABABBABA型的回文日期。

2）题目解析

题目要求
- 找出给定日期后的下一个回文日期和下一个ABABBABA型的回文日期。
解题思路
- 枚举日期: 从给定日期的下一天开始，逐日枚举，检查每个日期是否是回文日期或ABABBABA型的回文日期。
- 日期合法性检查: 在枚举过程中，需检查日期是否合法，包括月份天数和闰年情况。
- 字符串操作: 需要将整数日期转换为指定格式的字符串，以及将字符串日期转换为整数，以便进行比较和判断。
辅助函数
- int转string: 将整数转换为指定位数的字符串，用于构造日期字符串。
- string转int: 将字符串转换为整数，用于日期比较。
- 判断闰年: 根据年份判断是否是闰年，以确定2月的天数。
- 判断日期合法: 根据月份和年份判断日期是否合法。
- 判断回文: 检查字符串是否是回文。
- 判断ABABBABA型回文: 检查字符串是否是ABABBABA型的回文。
注意事项
- 枚举范围: 年份范围需设定合理，题目中暗示年份不会超过9999。
- 月份和日期范围: 月份为1-12，日期根据月份和是否闰年确定。
- 性能优化: 枚举过程中可跳过明显不合法的日期，如月份超出12或日期超出该月最大天数。
- 示例: 20200202后的下一个回文日期是20211202，下一个ABABBABA型的回文日期是21211212。

3）代码实现与测试

代码框架
- 主函数: 读取输入日期，初始化变量，开始枚举。
- 枚举循环: 逐年、逐月、逐日枚举，调用辅助函数进行判断。
- 输出结果: 找到目标日期后输出。
测试与调试
- 测试用例: 包括普通回文日期和ABABBABA型回文日期的测试。
- 边界情况: 如年份、月份、日期边界，闰年与非闰年切换等。
- 通过情况: 提交代码后，需关注通过率和运行时间，对未通过案例进行分析和调试。

4）总结

知识点回顾: 回文日期、日期合法性检查、字符串操作、枚举算法。
解题技巧: 合理利用辅助函数，注意枚举范围和性能优化。
扩展思考: 如何进一步优化算法，减少不必要的枚举？
课程结束: 本节课讲解到此结束，下节课将继续探讨相关话题。

三、知识小结

知识点	核心内容	考试重点/易混淆点	难度系数
模拟算法介绍	模拟算法通过模拟实际情况来解决问题，易理解但实现复杂，需细心处理细节。	模拟算法的特点、适用场景及实现注意事项。	🌟🌟🌟
扫雷问题讲解	遍历每个位置，特判地雷情况，扫描九宫格更新地雷数量。	如何准确扫描九宫格并更新地雷数量，避免遗漏或重复计算。	🌟🌟
灌溉问题讲解	使用两个二维数组分别表示当前和后一分钟的灌溉情况，持续更新。	如何正确更新灌溉情况，确保时间顺序不乱。	🌟🌟🌟
回文日期查找	枚举日期，判断是否为回文或AB ab baba型回文，需处理日期合法性、闰年判断等。	日期枚举方法、回文判断逻辑、日期合法性及闰年判断。	🌟🌟🌟🌟
字符串处理技巧	在模拟题中，string数据类型非常常用且好用，需掌握字符串的分割、转换、判断等操作。	字符串与整数之间的转换，字符串的子串操作，以及回文判断等。	🌟🌟🌟
日期合法性判断	根据年份、月份、日期以及闰年情况，判断日期是否合法。	闰年的判断规则，每个月的天数，以及日期范围的界定。	🌟🌟🌟
细节处理	模拟题中细节较多，如边界情况处理、数组越界检查、特殊条件判断等。	如何细心处理各种细节，避免因为小错误导致整个问题无法解决。	🌟🌟🌟🌟🌟

四、二分法

1. 二分法简介

1）二分法定义与性质

定义: 二分法是一种高效的查找方法，通过将问题的搜索范围一分为二，迭代地缩小搜索范围，直到找到目标或确定目标不存在。
适用条件: 有序数据集合。
效率: 每次迭代可以将搜索范围缩小一半，一般可以将
O(n)O(n)O(n)的枚举优化到

O(log⁡n)O(\log n)O(logn)
本质: 二分法本质上也是枚举，但利用数据结构的单调性减少了很多不必要的枚举。
类型: 常见的二分类型有整数二分、浮点二分和二分答案（最常见）。

2）二分法解题步骤

步骤一: 研究并发现数据结构（或答案变量）的单调性。
步骤二: 确定最大区间[l,r]，确保分界点一定在里面。若以r作为答案，答案区间在
[l+1,r]；若以l作为答案，答案区间在[l,r−1]。
步骤三: 确定check函数，一般为传入mid（区间中某个下标），返回mid所属区域或返回一个值。当check函数较简单时可以直接判断。
步骤四: 计算中点mid=(l+r)/2，用check判断该移动l或r指针，具体移动哪个需要根据单调性以及要求的答案来判断。
步骤五: 返回l或r，根据题意判断。

2. 解题步骤

1）整数二分

整数二分模板

while (l < r) {int mid = l + r >> 1;if (a[mid] >= x) r = mid;else l = mid + 1;
}

解释: 当l < r时，计算中间位置mid，如果a[mid]大于等于目标值x，则r移动到mid，否则l移动到mid + 1。最终l和r会收敛到相邻位置，此时r指向的就是第一个大于等于x的位置。
例题

#include<iostream>
using namespace std;
int main() {int data[200];for (int i = 0; i < 200; i++) {data[i] = i * 2 + 6;}int x;cin >> x;int l = -1, r = 199;while (l < r) {int mid = l + r + 1 >> 1;if (data[mid] >= x) r = mid - 1;else l = mid;}cout << r << endl;return 0;
}

注意: 初始化l为-1，r为数组最后一个元素的下标。在循环中，mid的计算方式为l + r + 1 >> 1，这是为了确保mid向上取整。当data[mid]大于等于x时，r移动到mid - 1，否则l移动到mid。最终输出r即为答案。
测试: 通过输入不同的x值，验证代码的正确性。例如，输入252，输出应为126；输入3，输出应为1。

3）浮点二分

浮点二分简介
- 概念: 浮点二分不再是在有序数组上做二分查找，而是在某个实数范围内进行查找。
- 原理: 实数域本身是单调的，所以也满足单调性。
- 与整数二分的区别: 使用的变量类型、退出的判断条件不同。
浮点二分模板
- 目标: 计算单调函数f(x)的零点。
- 初始化:
  double⁡l=0,r=169，eps⁡=1e−6（eps是一个极小量，设置为1e-6较合适）。
- 判断条件:
  while (r−l>=eps)，保证l，r最终一定收敛到分界点。
- 计算中点:
  double mid=(l+r)/2;
- 调整范围:
  - 若f(mid) >= 0，说明mid偏大了，需要减小mid，即r=mid；
  - 否则，l=mid。
- 返回结果: 最后返回l或r，两者差别不大。
- 注意: 浮点二分中，l和r最终会指向几乎同一个数字，因为浮点数不存在“相邻”的情况，它们会非常接近。

4）二分答案

二分答案模板
例题
14:17

二、知识小结

知识点	核心内容	考试重点/易混淆点	难度系数
二分法简介	二分法是一种高效的查找方法，通过将搜索范围一分为二，迭代缩小范围，适用于有序数据集合	二分法定义、适用场景	中
整数二分	在有序数组上进行二分查找，找出某个值的位置或分界点	查找过程、边界处理	中
浮点二分	在实数范围内进行查找，搜索范围从数组变为实数域	实数域单调性、退出条件	中
二分答案	最常见且重要的题型，需发现单调函数并进行二分	单调性判断、check函数设计	高
例题：跳石头	通过二分最短跳跃距离，计算需移走的石头数量，找到最远跳跃距离	最短跳跃距离与移石数量的关系、二分框架应用	高
例题：肖恩的苹果林	二分最近距离，判断能否种下至少m棵树苗	最近距离与种树数量的负相关关系	中
例题：乘法表问题	二分元素大小，利用矩阵规律计算排名，找到dk大的元素	矩阵规律、排名计算	高

五、贪心

一、贪心算法介绍

1. 学习目标

理解贪心算法: 理解贪心算法的基本概念和原理。
掌握贪心思路: 掌握贪心算法的基本思想和解题思路。
分析贪心问题: 理解常见的贪心模型，并能够分析并解决简单的贪心问题。

2. 贪心的基本原理

局部最优解: 每一步都选择局部最优解，尽量不考虑对后续的影响，最终达到全局最优解。

3. 贪心的局限性

局限性: 贪心算法不能保证获得全局最优解，但在某些问题上具有高效性。

4. 贪心的特征

贪心选择性质: 问题中要能找到当前的最好决策。
最优子结构性质: 可以通过局部最优推到全局最优。具有“不同的操作产生的贡献相同”或“操作次数固定”的特征时，每次选择代价最小的操作。

5. 贪心的类型

类型多且杂: 贪心的类型多样且复杂，难以划分，需要大量的练习和积累来掌握。

二、贪心算法实现步骤

1. 确定问题的最优子结构

最优子结构: 贪心算法往往和排序、优先队列等一起出现。在当前情况下，选择局部最优，然后不断往后推，最终推到一个全局最优，这样的结构就是最优子结构。

2. 构建贪心选择的策略

构建策略: 可能通过“分类讨论”、“最小代价”、“最大价值”等方式来思考贪心策略。
验证正确性: 简单验证贪心的正确性，常用句式是“这样做一定不会使得结果变差”或“不存在比当前方案更好的方案”等。

3. 通过贪心选择逐步求解问题

逐步求解: 通过贪心选择，逐步求解问题，直到得到最终解。

4. 例题

1）题目解析

建议通过大量练习来加深对贪心算法的理解和掌握。

三、常见贪心模型和例题

1. 例题

1）题目描述

题目背景: 小蓝是机甲战队的队长，需要将n名队员分成两组a和b。
分组条件: 每个队友都属于a组或b组；a组和b组都不为空。
目标: 使得两组的战斗力差距最小。

2）解题思路

排序与划分
- 排序: 首先对队员的战斗力进行排序。
- 划分: 排序后，找一个位置进行划分，使得左边的都在a组，右边的都在b组。
- 差距计算: 战斗力差距即为划分位置两边的战斗力之差。
枚举与最小值
- 枚举: 由于差距的取值仅有n-1种，因此可以通过枚举每一个划分位置来找出所有可能的差距。
- 最小值: 从所有可能的差距中取出最小值，即为可以得到的最小战斗力差距。
启示
- 处理混乱数据: 当数据混乱且不好处理时，尝试先排序再分析。
- 排序不影响答案: 在本题中，排序是解决问题的关键，且排序不影响最终答案。

3）代码实现

输入: 首先输入队员个数n，然后输入n个整数表示每名队员的战斗力值。
初始化: 初始化答案ans为a[2]-a[1]，因为至少需要两个队员。
排序: 对战斗力数组进行排序。
枚举: 遍历每一个划分位置，更新ans为当前位置两边的战斗力之差的最小值。
输出: 输出最小战斗力差距ans。

4）题目解析

审题: 明确题目要求，即计算最小战斗力差距。
思路: 通过排序和枚举来找到最小差距。
答案: 输出一个整数，表示可以得到的最小战斗力差距。
测试用例: 题目提供了多个测试用例，确保代码的正确性。

5）总结

关键点: 排序、枚举、最小值。
启示: 当面对混乱且不易处理的数据时，排序可能是一个有效的解决策略。
应用: 本题的方法可以推广到其他需要分组并最小化组间差距的问题中。

2. 例题

1）题目背景

问题背景: 在很久很久以前，有n个部落居住在平原上，依次编号为1到n。第i个部落的人数为
tit_iti
。有一年发生了灾荒，年轻的政治家小蓝想要说服所有部落一同应对灾荒，通过谈判合并部落。
合并规则: 每次谈判只能邀请两个部落参加，花费的金币数量为两个部落的人数之和。谈判后，两个部落联合成一个新的部落，人数为原来两个部落的人数之和。
目标: 经过n-1次谈判，将所有部落合并成一个部落，并使得总花费的金币数量最小。

2）贪心策略

贪心思想: 每次选择代价最小的两个部落进行合并，不仅可以使得当前合并的代价小，还可以使得后续合并代价也尽可能小。
原因: 最小的两个部落合并后的新部落，其人数一定是最小的（相比其他合并方案），因此后续合并时，这个新部落与其他部落合并的代价也会相对较小。

3）实现方法

数据结构: 使用优先队列（小根堆）来维护部落的大小，以便每次都能快速找到最小的两个部落。
具体步骤:

1. 初始化一个优先队列，并将所有部落的人数加入队列。
2. 当队列中的部落数量大于1时，执行以下步骤：

- - 弹出队列中的最小两个部落（记为x和y）。
  - 计算合并这两个部落的代价（即x+y）。
  - 将合并后的新部落（人数为x+y）加入队列。
  - 累加合并代价到总花费中。

1. 当队列中只剩下一个部落时，输出总花费。

4）题型(蓝桥OJ545谈判)

题目解析
- 输入描述:
  - 第一行包含一个整数n，表示部落的数量。
  - 第二行包含n个正整数，依次表示每个部落的人数。
- 输出描述: 输出一个整数，表示最小花费。
- 输入输出样例:
  - 输入: 9 1 3 5 32
  - 输出: 31
- 解题思路: 按照上述贪心策略和实现方法，使用优先队列维护部落大小，并逐次合并最小的两个部落，直到所有部落合并为一个。最后输出总花费。
- 易错点:
  - 注意初始化优先队列时，应使用小根堆（即greater关键字）。
  - 确保每次合并后都将新部落的人数加入优先队列中。
  - 最后输出的总花费应为所有合并代价的累加和。

3. 例题

13:47

1）题目背景

背景: 元旦快到了，校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加会的同学所获得的纪念品价值相对均衡，他要把购来的纪念品根据价格进行分组，但每组最多只能包括两件纪念品，并且每组纪念品的价格之和不能超过一个给定的整数。

2）题目要求

目标: 为了保证在尽量短的时间内发完所有纪念品，乐乐希望分组数目最少。需要找出一个程序，找出所有分组方案中分组数最少的一种，并输出最少分组数目。
输入:
- 第一行包括一个整数
  www
  （
  80≤w≤20080 \leq w \leq 20080≤w≤200
  ），为每组纪念品价格之和的上限。
- 第二行为一个整数
  nnn
  （
  1≤n≤300001 \leq n \leq 300001≤n≤30000
  ），表示购来的纪念品的总件数。
- 第
  3∼n+23 \sim n + 23∼n+2
  行每行包含一个正整数
  pip_ipi
  （
  5≤pi≤w5 \leq p_i \leq w5≤pi≤w
  ），表示所对应纪念品的价格。
输出: 输出一行，包含一个整数，即最少的分组数目。

3）解题思路

贪心策略
正确性证明
- 证明: 每次选择最贵的和最便宜的纪念品进行组合，可以确保在有限的空间内尽可能多地装入纪念品，从而减少分组数目。如果选择不是最贵的和最便宜的组合，那么可能会留下一些空间未被利用，导致分组数目增加。
实现细节
- 排序: 使用C++的sort函数对纪念品价格进行排序。
- 双指针: 初始化两个指针，一个指向价格数组的起始位置（最便宜的纪念品），一个指向价格数组的末尾位置（最贵的纪念品）。
- 循环判断: 在循环中判断两个指针所指向的纪念品价格之和是否小于等于
  www
  ，如果是，则将它们分为一组，并同时移动两个指针；如果不是，则只移动最贵纪念品的指针。
- 输出结果: 循环结束后，输出分组数目。

4）题目解析

审题: 仔细阅读题目，理解题目要求和输入输出格式。
思路: 采用贪心策略，每次选择最贵的和最便宜的纪念品进行组合，以减少分组数目。
实现: 编写C++代码实现上述思路，注意排序和双指针的使用。
调试: 对代码进行调试，确保能够正确输出最少分组数目。
答案: 提交代码并通过测试，得到最少分组数目作为答案。

4. 例题

19:45

1）题目背景

题目背景: 肖恩老师要给表现出色的算法班同学们分发n个不同种类的糖果，每个糖果用一个小写阿拉伯字母表示。要求每个同学至少分到一个糖果，且希望同学们分到的糖果组成的字符串的字典序最大可能小。

2）解题思路

排序
- 排序: 首先对糖果字符串进行排序。
分类讨论
- 分类讨论:
  - 情况一（全相等）: 如果所有糖果都相同（如全为a），则尽量平均分配给每个同学，使得每个同学分到的字符串长度尽可能相等。
    - 举例: 如果有7个a要分给3个同学，最优分配是“aa, aa, aaa”而不是“aaaaa, a, a”。
  - 情况二（
    s[x]==s[1]s[x] == s[1]s[x]==s[1]
    ）: 如果第x个糖果与第一个糖果相同，说明从第一个糖果到第x个糖果可以作为一个整体分配给最后一个同学，以达到最小化最大字典序的目的。
    - 举例: 字符串为“aaabcc”，分给3个同学，最优分配是“aa, a, bcc”。
  - 情况三（
    s[x]!=s[1]s[x] != s[1]s[x]!=s[1]
    ）: 如果第x个糖果与第一个糖果不同，那么将
    s[x]s[x]s[x]
    及其后面的所有糖果全部分配给最后一个同学，前面的糖果依次分配给前面的同学。
    - 举例: 字符串为“aabccd”，分给3个同学，最优分配是“aa, b, ccd”。

3）题型(蓝桥云课分糖果问题)

题目解析
- 输入: 第一行输入两个整数n和x，分别表示糖果的数量和同学的数量。第二行输入一个长度为n的字符串，表示糖果的种类。
- 输出: 输出一个字符串，表示所有糖果分配给同学后，字典序最大的字符串的最小可能值。
- 解题思路: 如上所述，先排序，然后根据糖果的种类和同学的数量进行分类讨论，找到最优的分配方案。
- 答案: 通过贪心策略，可以找到使得字典序最大的字符串最小可能的分配方案。

4）实现细节

实现步骤:

1. 输入n和x，以及糖果字符串s。
2. 对字符串s进行排序。
3. 根据排序后的字符串和同学的数量x，进行分类讨论，找到最优的分配方案。
4. 输出最优分配方案中字典序最大的字符串。

代码示例:
注意: 在实现时，需要注意字符串的处理和边界条件的判断，确保算法的正确性和健壮性。

四、知识小结

知识点	核心内容	考试重点/易混淆点	难度系数
贪心算法介绍	贪心算法的基本概念和原理，贪心算法的基本思想和解题思路	贪心算法与全局最优解的关系，贪心选择性质与最优子结构的理解	中
贪心算法的实现步骤	确定问题的最优子结构，构建贪心选择的策略，通过贪心选择逐步求解问题	最优子结构的识别，贪心选择策略的构建与验证	中
常见的贪心模型	最小化战斗力差距模型，最小代价合并模型，最小化分组数目模型	排序在贪心算法中的应用，贪心策略的选择与优化	中
贪心算法实例解析	蓝桥oj三四幺二最小化战斗力差距，蓝桥oj五四五谈判合并部落，纪念品分组问题	如何通过排序简化问题，如何构建有效的贪心策略，贪心策略的正确性验证	高
贪心算法的特殊应用	字符串分配问题中的贪心策略，找规律的贪心问题	字符串分配中的字典序问题，特殊贪心问题的识别与解决	高
注：难度系数分为低、中、高三个等级，以反映各知识点的掌握难度和考试重要性。

精准客户信息一条多少钱_网站搭建东莞_谷歌google play官网_如何做推广推广技巧

一、双指针

1、双指针算法概述

2、对撞指针

简介

求解步骤

例题

3、快慢指针

简介

求解步骤

例题

4、总结

二、快速排序

1、快速排序的思想

2、快速排序的实现

3、快速排序的实现（Partition函数）

4、快速排序的实现（图示）

5、例题讲解（蓝桥云课）

三、模拟

一、模拟算法介绍

1. 模拟算法概述

2. 模拟算法的风格

3. 例题(蓝桥oj五四九扫雷)

1）题目解析

二、例题

1）题目描述

2）题目解析

3）代码实现

3. 例题

1）题目描述

2）解题思路

3）关键点与细节

4）题目解析

4. 例题﻿

1）回文日期

2）题目解析

3）代码实现与测试

4）总结

三、知识小结

四 、二分法

1. 二分法简介

1）二分法定义与性质

2）二分法解题步骤

2. 解题步骤

1）整数二分

3）浮点二分

4）二分答案

二、知识小结

五、贪心

一、贪心算法介绍

1. 学习目标

2. 贪心的基本原理

3. 贪心的局限性

4. 贪心的特征

5. 贪心的类型

二、贪心算法实现步骤

1. 确定问题的最优子结构

2. 构建贪心选择的策略

3. 通过贪心选择逐步求解问题

4. 例题

1）题目解析

三、常见贪心模型和例题

1. 例题

1）题目描述

2）解题思路

3）代码实现

4）题目解析

5）总结

2. 例题

1）题目背景

2）贪心策略

3）实现方法

4）题型(蓝桥OJ545谈判)

3. 例题

1）题目背景

2）题目要求

3）解题思路

4）题目解析

4. 例题

1）题目背景

4. 例题

四、二分法