数据结构05：树与二叉树习题02[C++]

考研笔记整理，本篇作为二叉树的入门习题，供小伙伴们参考~🥝🥝

之前的博文链接在此：数据结构05：树与二叉树[C++]-CSDN博客~🥝🥝

第1版：王道书的课后习题~🧩🧩

编辑：梅头脑🌸

代码指导：文心一言

习题来源：王道考研《2025年数据结构考研复习指导》

🧵01-02 二叉树的先序序列与后序序列

🧵03 后序遍历二叉树非递归算法

🧵04 二叉树逆向层次遍历

🧵05 非递归算法求二叉树高度

🧵06 判断完全二叉树

🧵07 判断双分支节点个数

🧵08 交换二叉树左右子树

🧵09 先序遍历第k个节点的值

🧵10 删除子树

🧵11 寻找祖先节点

🧵12 寻找公共祖先节点

🧵13 求非空二叉树的宽度

🧵14 已知先序求后序

🧵15 串联叶节点

🧵16 判断二叉树相似

🧵17 二叉树带权路径长度

🧵18 二叉树带权路径长度

🧵19 判断是否为二叉树搜索树

🔚结语

🧵01-02 二叉树的先序序列与后序序列

🧩题目

1 若某非空二叉树的先序序列和后序序列正好相反，则该二又树的形态是什么?

2 若某非空二叉树的先序序列和后序序列正好相同，则该二又树的形态是什么?

📇解题思路

1 树中除了叶节点外，每个节点的度为1。

2 根左右 = 左右根，啊这，要么节点是一样的（...），要么只有根节点。

🧵03 后序遍历二叉树非递归算法

🧩题目

编写后序遍历二叉树的非递归算法。

📇解题思路

深度优先遍历中的后序遍历，按照左、右、根的顺序访问二叉树节点。在非递归实现中，我们需要借助栈来辅助我们进行遍历。

为了避免在回溯时重复访问节点，特别是右子节点，我们可以使用一个辅助指针r。当我们遍历完一个节点的右子树后，用r标记这个节点，表示已经“已阅”。这样，在回溯时若遇到已标记的节点，我们就不会再次访问其右子节点。

⌨️解题代码

以下是王道书标准答案的解法代码~

#include<iostream>
#include<stack>
using namespace std;typedef struct BiTNode{int data;BiTNode* lchild, *rchild;BiTNode() :data(0), lchild(nullptr), rchild(nullptr){}BiTNode(int x) :data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}bool visit(int val) {cout << val << " ";return true;
}void post_order(BiTNode* root) {if (!root) return;stack<BiTNode*> st;   // 用于存放节点的栈BiTNode* p = root;    // 用于记录上一次访问的节点  BiTNode* r = nullptr; // 用于记录右子节点cout <<  "后序遍历：" ;while (p != nullptr || !st.empty()) {   // 当前节点不为空或者栈不为空if (p != nullptr) {                 // 当前节点不为空st.push(p);                     // 当前节点入栈p = p->lchild;				    // 访问左子节点}else {p = st.top();                                   // 获取栈顶元素if (p->rchild != nullptr && p->rchild != r) {   // 右子节点存在且未被访问p = p->rchild;      	    // 访问右子节点} else {st.pop();                   // 弹出栈顶元素visit(p->data);			    // 访问栈顶元素r = p;  			        // 记录上一次访问的节点p = nullptr;			    // 当前节点置空}}}
}int main() {BiTNode* root = create_tree();post_order(root);return 0;
}

📇友情配图

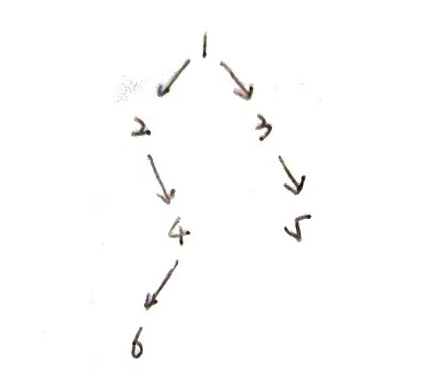
📇代码演示

访问根节点1，入栈；访问节点1的左子结点2，入栈；访问节点2的右子结点4，入栈，访问节点4的左子结点6，入栈；
- 目前辅助栈：1 2 4 6；
- 目前已输出：无；
节点6没有孩子节点，输出节点6；并将指针r指向节点6，表示”已阅“；并将节点p置空；
- 目前辅助栈：1 2 4；
- 目前已输出：6；
根据辅助栈向节点4回溯，节点4没有右孩子，输出节点4；并将指针r指向节点4，表示”已阅“；并将节点p置空；
- 目前辅助栈：1 2；
- 目前已输出：6 4；
根据辅助栈向节点2回溯，节点2有右孩子，但是因为指针r已经给节点4打上”已阅“的戳，所以并不会再次返回节点4，而是输出节点2；并将指针r指向节点2，表示”已阅“；并将节点p置空；
- 目前辅助栈：1；
- 目前已输出：6 4 2；
根据辅助栈向节点1回溯，节点1有右孩子，而且没有遍历过，所以先将节点3入栈；同理，节点5入栈；
- 目前辅助栈：1 3 5；
- 目前已输出：6 4 2；
同样的，回溯节点5，r指向5；回溯节点3，r指向3，回溯节点1，r指向1；1出栈后栈空，结束遍历；
- 目前辅助栈：空；
- 目前已输出：6 4 2 5 3 1；

📇相关知识

对于二叉树的遍历，我们通常有三种基本的深度优先遍历方法：先序遍历、中序遍历和后序遍历。这些遍历方法的递归实现相对直观，但在某些情况下，我们可能需要非递归的实现方式，特别是当我们需要避免递归调用的开销或者深入理解遍历过程时。

非递归实现主要依赖于栈这种数据结构来辅助我们追踪需要访问的节点。以下是三种遍历方法的非递归实现及其特点：

后序遍历（左、右、根）：
- 需要使用辅助指针r来避免重复访问右子节点。
- 在每个节点访问其右子节点之后，用r标记该节点，以防止在回溯时重复访问。
- 遍历过程中需要不断地将节点压入和弹出栈，同时利用p指针进行节点的回溯（p在访问完栈顶元素后需要置空）。
先序遍历（根、左、右）：
- 访问顺序是先访问根节点，然后访问左子树，最后访问右子树。
- 不需要使用辅助指针r，因为没有重复访问的问题。
- 在访问节点时，首先访问当前节点，然后将当前节点压栈，并转向其左子节点。当左子树访问完毕后，从栈中弹出节点，并转向其右子节点。
中序遍历（左、根、右）：
- 访问顺序是先访问左子树，然后访问根节点，最后访问右子树。
- 同样不需要使用辅助指针r。
- 在访问过程中，先将节点压栈，然后转向其左子节点。当左子树访问完毕后，从栈中弹出节点并访问，然后转向其右子节点。

下面是三种遍历方法的代码实现，以及main函数中创建二叉树并调用这些遍历方法的示例：

#include<iostream>
#include<stack>
using namespace std;typedef struct BiTNode{int data;BiTNode* lchild, *rchild;BiTNode() :data(0), lchild(nullptr), rchild(nullptr){}BiTNode(int x) :data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}bool visit(int val) {cout << val << " ";return true;
}void post_order(BiTNode* root) {if (!root) return;stack<BiTNode*> st;   // 用于存放节点的栈BiTNode* p = root;    // 用于记录上一次访问的节点  BiTNode* r = nullptr; // 用于记录右子节点cout <<  "后序遍历：" ;while (p != nullptr || !st.empty()) {   // 当前节点不为空或者栈不为空if (p != nullptr) {                 // 当前节点不为空st.push(p);                     // 当前节点入栈p = p->lchild;				    // 访问左子节点}else {p = st.top();                                   // 获取栈顶元素if (p->rchild != nullptr && p->rchild != r) {   // 右子节点存在且未被访问p = p->rchild;      	    // 访问右子节点} else {st.pop();                   // 弹出栈顶元素visit(p->data);			    // 访问栈顶元素r = p;  			        // 记录上一次访问的节点p = nullptr;			    // 当前节点置空}}}cout << endl;
}void pre_order(BiTNode* root) {if (!root) return;stack<BiTNode*> st;   // 用于存放节点的栈BiTNode* p = root;    // 用于记录上一次访问的节点  cout << "先序遍历：";while (p != nullptr || !st.empty()) {   // 当前节点不为空或者栈不为空if (p != nullptr) {                 // 当前节点不为空visit(p->data);                 // 访问当前节点st.push(p);                     // 当前节点入栈p = p->lchild;				    // 访问左子节点}else {p = st.top();                   // 获取栈顶元素st.pop();                       // 弹出栈顶元素p = p->rchild;      	        // 访问右子节点}}cout << endl;
}void in_order(BiTNode* root) {if (!root) return;stack<BiTNode*> st;   // 用于存放节点的栈BiTNode* p = root;    // 用于记录上一次访问的节点  cout << "中序遍历：";while (p != nullptr || !st.empty()) {   // 当前节点不为空或者栈不为空if (p != nullptr) {                 // 当前节点不为空st.push(p);                     // 当前节点入栈p = p->lchild;				    // 访问左子节点}else {p = st.top();                   // 获取栈顶元素st.pop();                       // 弹出栈顶元素visit(p->data);                 // 访问当前节点p = p->rchild;      	        // 访问右子节点}}cout << endl;
}
int main() {BiTNode* root = create_tree();post_order(root);pre_order(root);in_order(root);return 0;
}

再次总结三种非递归遍历方式：

后序遍历需要使用辅助指针来避免重复访问；先序和中序遍历则不需要，因为它们都是最后访问右子节点。
在非递归实现中，栈都起到了关键的作用，它帮助我们追踪需要回溯到的节点。
通过调整访问节点和入栈、出栈的顺序，我们可以实现不同的遍历方式。

🧵04 二叉树逆向层次遍历

🧩题目

试给出二叉树的自下而上、从右到左的层次遍历算法。

📇解题思路

层次遍历的基础上，增加一个栈实现逆向输出的效果~

⌨️解题代码

#include<iostream>
#include<queue>
#include<stack>
using namespace std;typedef struct BiTNode{int data;BiTNode* lchild, *rchild;BiTNode() :data(0), lchild(nullptr), rchild(nullptr){}BiTNode(int x) :data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}bool visit(int val) {cout << val << " ";return true;
}void post_sequence(BiTNode* root) {if (!root) return;queue<BiTNode*> qu;   // 用于存放节点的队stack<BiTNode*> st;   // 用于存放节点的栈BiTNode* p = root;    // 用于记录上一次访问的节点  cout <<  "层序遍历 自下而上 从右到左：" ;qu.push(p);while (!qu.empty()) { // 在层序遍历的基础上，将节点存入栈中p = qu.front();qu.pop();st.push(p);if (p->lchild != nullptr) {             qu.push(p->lchild);                 }if (p->rchild != nullptr) {                qu.push(p->rchild);                     }}while (!st.empty()) {p = st.top();st.pop();visit(p->data);}
}int main() {BiTNode* root = create_tree();post_sequence(root);return 0;
}

🧵05 非递归算法求二叉树高度

🧩题目

假设二叉树采用二叉链表存储结构，设计一个非递归算法求二叉树的高度。

📇解题思路

广度遍历与深度遍历都可以用于求树的高度~

以层次遍历tree_depth1为例，只需要增加一层循环即可完成求树高度的操作：嵌套for循环用于控制下一层的节点数量，在遍历每层的树节点后，树的深度depth++~~

以深度遍历tree_depth2为例，增加深度参数，只需要在先序遍历时，遍历下一层时深度+1，即可完成求树高度的操作，这样仅限于输出数据。如果想增加返回值，则需要在遍历到深度分支最后一个数据（本树为节点6与节点5时）回归时，统计子树的深度，+1即为本树的深度~~

⌨️解题代码

#include<iostream>
#include<queue>
using namespace std;typedef struct BiTNode{int data;BiTNode* lchild, *rchild;BiTNode() :data(0), lchild(nullptr), rchild(nullptr){}BiTNode(int x) :data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}bool visit(int val) {cout << val << " ";return true;
}// 层序遍历
int tree_depth1(BiTNode* root) {if (!root) return 0;queue<BiTNode*> qu;   // 用于存放节点的队BiTNode* p = root;    // 用于记录上一次访问的节点  cout << "——二叉树层次遍历求树的深度——" << endl;int depth = 1;qu.push(p);while (!qu.empty()) {int size = qu.size();for (int i = 0; i < size; i++) {p = qu.front();qu.pop();cout << "二叉树节点数据: " << p->data << ", ";cout << "二叉树节点深度: " << depth << endl;if (p->lchild != nullptr) {qu.push(p->lchild);}if (p->rchild != nullptr) {qu.push(p->rchild);}}depth++;}return depth - 1;
}// 先序遍历，没有返回值
void tree_depth2(BiTNode* root, int depth) {if (!root) return ;cout << "二叉树节点数据: " << root->data << ", ";cout << "二叉树节点深度: " << depth << endl;tree_depth2(root->lchild, depth + 1);tree_depth2(root->rchild, depth + 1);
}// 先序遍历，具有返回值
int tree_depth3(BiTNode* root, int depth) {if (root == nullptr) return 0;cout << "二叉树节点数据: " << root->data << ", ";cout << "二叉树节点深度: " << depth << endl;int left_depth = tree_depth3(root->lchild, depth + 1);int right_depth = tree_depth3(root->rchild, depth + 1);cout << "当前节点: " << root->data << ", ";cout << "左子树深度: " << left_depth << ", ";cout << "右子树深度: " << right_depth << ", ";int tree_depth = (left_depth > right_depth) ? left_depth + 1 : right_depth + 1;cout << "树的高度: " << tree_depth << endl;return tree_depth;
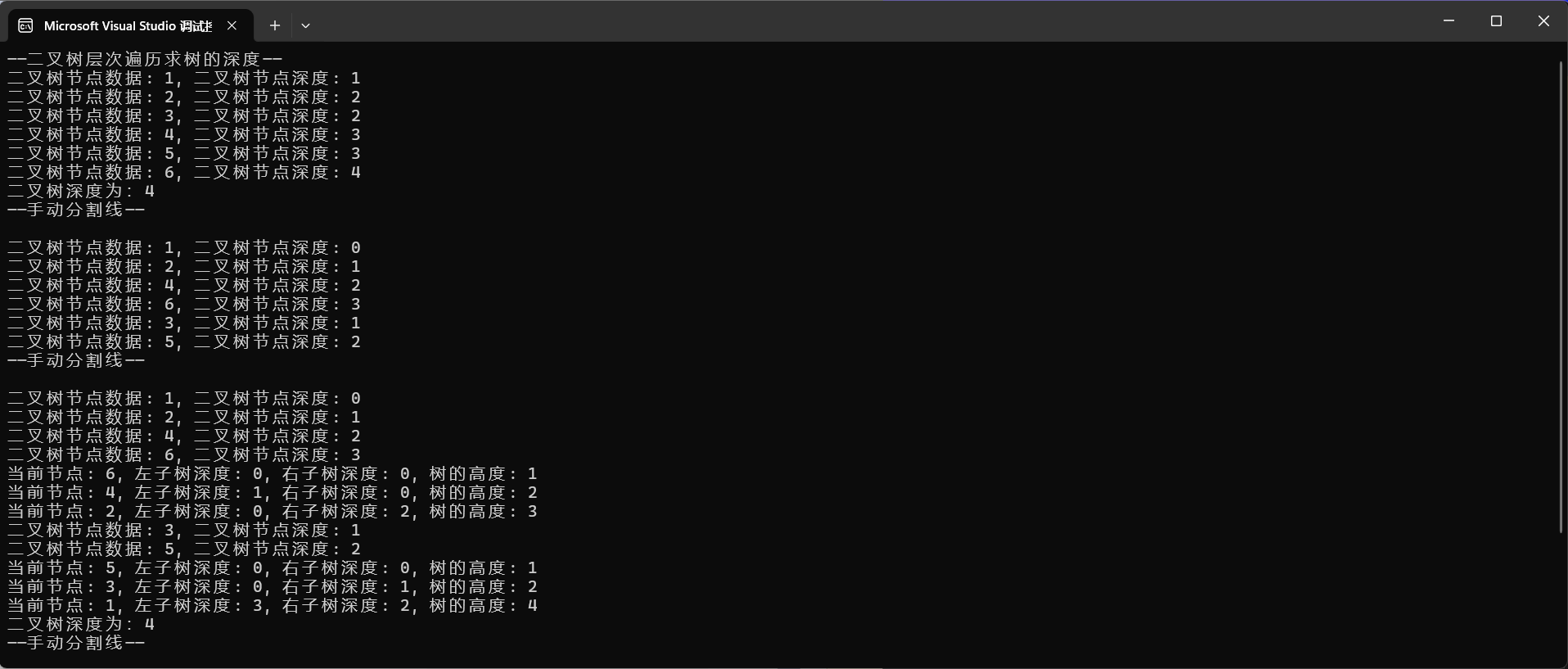
}int main() {BiTNode* root = create_tree();cout << "二叉树深度为：" << tree_depth1(root) << endl;cout << "——手动分割线——" << endl << endl;tree_depth2(root,0);cout << "——手动分割线——" << endl << endl;cout << "二叉树深度为：" << tree_depth3(root, 0) << endl;cout << "——手动分割线——" << endl << endl;return 0;
}

🧵06 判断完全二叉树

🧩题目

二叉树按二叉链表形式存储，试编写一个判别给定二叉树是否是完全二又树的算法。

📇解题思路

我们以下面4个可爱的小树为例：

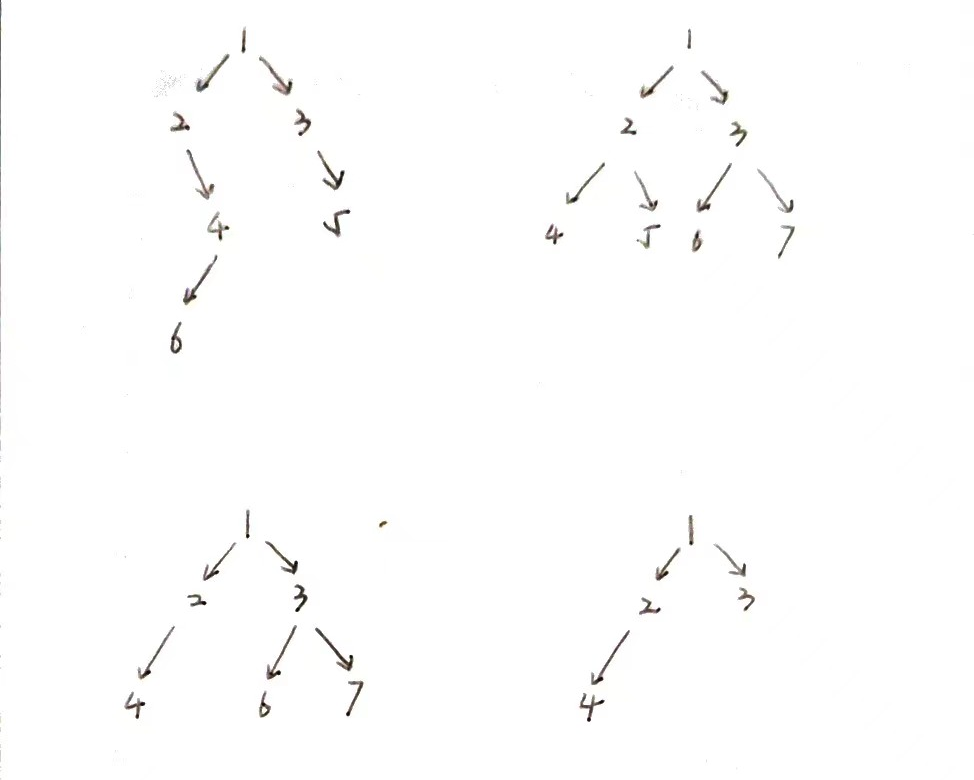
首先，这种题目，应该是层次遍历方便一些。

如果，从树的结构考虑，我们判断这棵树是否是完全二叉树，通常看这样几个方面：1）是不是有两个左子树孤儿；2）是不是有一个右子树孤儿；3）孤儿的位置是不是拴在本层的最后一个节点。如果按照这个方法判断，我们会得到一个很麻烦的解法，如以下代码1；

（究竟是哪个小可爱想出这么蠢的解法？哦，是我自己😑~）

但是，如果利用层次遍历的结果，这件事情就好办很多，例如最难判断的树3，其层次遍历第3层的队列为：4 NULL 6 7，出队时有NULL节点，不符合完全二叉树的定义，因此直接判错，如以下代码2~

（这个聪明的解法是王道书的标准答案🐣~）

⌨️解题代码1（不推荐）

#include <iostream>  
#include <queue>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}BiTNode* create_tree2() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->lchild->rchild = new BiTNode(5);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}BiTNode* create_tree3() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}BiTNode* create_tree4() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);return root;
}bool visit(int val) {cout << val << " ";return true;
}bool is_complete(BiTNode* root) {if (!root) return true; // 空树被认为是完全二叉树      queue<BiTNode*> qu;bool end_of_level = false; // 标记当前层是否结束  bool isLeaf = false;     // 标记当前节点是否是叶子节点  qu.push(root);while (!qu.empty()) {BiTNode* current_node = qu.front();qu.pop();if (end_of_level && (current_node->lchild || current_node->rchild)) {   // 如果已经遇到当前层的结尾，则后面的节点都应该是叶子节点  return false;                                                       // 不是完全二叉树  }if (!current_node->lchild || !current_node->rchild) {                   // 如果当前节点没有左孩子或没有右孩子，则孩子节点必须是叶子节点isLeaf = true;                                                      // 当前节点的孩子节点是叶节点  }if (current_node->lchild) {                                             // 如果左孩子不为空，则入队qu.push(current_node->lchild);}else if (current_node->rchild) {                                        // 左孩子为空，但右孩子不为空，则不是完全二叉树  return false;}if (current_node->rchild) {										        // 如果右孩子不为空，则入队qu.push(current_node->rchild);}else {                                                                  // 如果当前节点是这一层的第一个没有右孩子的节点，则将endOfLevel设置为true，表示当前层后面的节点都应该是叶子节点 if (isLeaf) {end_of_level = true;}}isLeaf = false;                                                         // 重置isLeaf标志，为下一个节点做准备  }return true;
}int main() {BiTNode* root1 = create_tree1();BiTNode* root2 = create_tree2();BiTNode* root3 = create_tree3();BiTNode* root4 = create_tree4();if (is_complete(root1)) cout << "树root1是完全二叉树: " << endl;else cout << "树root1不是完全二叉树: " << endl;if (is_complete(root2)) cout << "树root2是完全二叉树: " << endl;else cout << "树root2不是完全二叉树: " << endl;if (is_complete(root3)) cout << "树root3是完全二叉树: " << endl;else cout << "树root3不是完全二叉树: " << endl;if (is_complete(root4)) cout << "树root4是完全二叉树: " << endl;else cout << "树root4不是完全二叉树: " << endl;return 0;
}

⌨️解题代码2

bool is_complete(BiTNode* root) {if (!root) return true; // 空树被认为是完全二叉树      queue<BiTNode*> qu;qu.push(root);while (!qu.empty()) {BiTNode* p = qu.front();qu.pop();if (p) {qu.push(p->lchild);qu.push(p->rchild);}else {while (!qu.empty()) {p = qu.front();if (p) return false;qu.pop();}}}return true;
}

🧵07 判断双分支节点个数

🧩题目

假设二叉树采用二叉链表存储结构存储，试设计一个算法，计算一棵给定二叉树的所有双分支结点个数。

📇解题思路

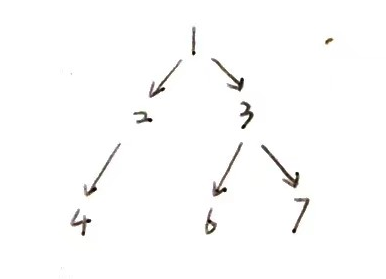
这种也可以用广度遍历和深度遍历两种算法实现~

⌨️解题代码（层序遍历）

#include <iostream>  
#include <queue>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}int double_branched(BiTNode* root) {if (!root) return 0;  queue<BiTNode*> qu;qu.push(root);int count = 0;while (!qu.empty()) {BiTNode* p = qu.front();qu.pop();if (p->lchild && p->rchild) {qu.push(p->lchild);qu.push(p->rchild);count++;cout << "双分支节点：" << p->data << endl;}else if (p->lchild) {qu.push(p->lchild);}else if (p->rchild) {qu.push(p->rchild);}}cout << "双分支节点个数：" << count << endl;return count;
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;double_branched(root1);cout << "——手动分割线——" << endl << endl;return 0;
}

⌨️解题代码2（先序遍历）

王道书答案，采用递归方式，如果遍历到双分支节点，则计数+1，否则继续向后遍历~

int double_branched(BiTNode* root) {if (root == nullptr) return 0;    else if (root->lchild != nullptr && root->rchild != nullptr) {cout << "双分支节点：" << root->data << endl;return double_branched(root->lchild) + double_branched(root->rchild) + 1;}else {return double_branched(root->lchild) + double_branched(root->rchild);}
}

🧵08 交换二叉树左右子树

🧩题目

设树B是一棵采用链式结构存储的二叉树，编写一个把树B中所有结点的左、右子树进
行交换的函数。

📇解题思路

这道题也可以用深度遍历与广度遍历两种算法实现~

⌨️解题代码（层序遍历+先序遍历）

#include <iostream>  
#include <queue>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}// 广度遍历
BiTNode* swap_childnode1(BiTNode* root) {if (root == nullptr) return root;  queue<BiTNode*> qu;qu.push(root);int count = 0;while (!qu.empty()) {BiTNode* p = qu.front();qu.pop();if (p->lchild != nullptr || p->rchild != nullptr) {swap(p->lchild, p->rchild);if (p->lchild != nullptr) qu.push(p->lchild);if (p->rchild != nullptr) qu.push(p->rchild);}}return root;
}// 深度遍历
BiTNode* swap_childnode2(BiTNode* root) {if (root != nullptr) {swap_childnode2(root->lchild);swap_childnode2(root->rchild);swap(root->lchild, root->rchild);}return root;
}// 输出
void level_order(BiTNode* root) {if (root == nullptr) return;queue<BiTNode*> qu;qu.push(root);while (!qu.empty()) {BiTNode* p = qu.front();qu.pop();cout << p->data << " ";if (p->lchild != nullptr) {qu.push(p->lchild);}if (p->rchild != nullptr) {qu.push(p->rchild);}}cout << endl;
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;cout << "原树层序遍历："; level_order(root1);root1 = swap_childnode1(root1);cout << "第1次交换层序遍历："; level_order(root1);root1 = swap_childnode2(root1);cout << "第1次交换层序遍历："; level_order(root1);cout << "——手动分割线——" << endl << endl;return 0;
}

🧵09 先序遍历第k个节点的值

🧩题目

假设二叉树采用二叉链存储结构存储，设计一个算法，求先序遍历序列中第 k(1<k<二叉树中结点个数)个结点的值。

📇解题思路

先序遍历有递归和非递归两种：

1）递归算法，有点小坑🕳，例如，我曾经用这样的代码执行先序遍历，当k遍历到1时，返回值，然后退出递归。这个代码看着是不是还挺简单易行的？

// 错误解法
int pre_order_kth(BiTNode* root, int k) {if (root != nullptr) {cout << "节点数据" << root->data << " ";cout << "k值" << k << endl;if (k == 1) {return root->data;}pre_order_kth(root->lchild, k - 1);pre_order_kth(root->rchild, k - 1);}
}

但是执行起来的结果却让人哭笑不得：

首先，k的值不会减少，而是在回退的时候根据系统的递归栈增加了，相当于计算的不是遍历到的序列，更像是节点在树中的 k - 节点高度；

其次，k == 1时根本不会停止循环直接退出，而是会继续向后遍历，直到遍历完整棵树为止，返回的节点永远是先序遍历的最后一个节点。

而我想到的第一种修正解法是，在k == 1时停止循环。这种算法的思想也很简单，增加判断的步骤：如果左子树中找到了节点，返回结点值；如果左子树没有找到，那么就从右子树中寻找；如果找到是空节点，则返回-1，避免在空节点处实现k值的更改；

// 错误解法2
int pre_order_kth2(BiTNode* root, int k) {if (root == nullptr) {return -1; }cout << "节点数据: " << root->data << " ";cout << "k值: " << k << endl;if (k == 1) {return root->data; }--k;int leftResult = pre_order_kth2(root->lchild, k); // 先递归左子树  if (leftResult != -1) {return leftResult;                           // 如果在左子树中找到了，就直接返回结果  }int rightResult = pre_order_kth2(root->rchild, k); // 如果左子树中没有找到，继续递归右子树  if (rightResult != -1) {return rightResult;                           // 如果在右子树中找到了，就直接返回结果  }
}

然后我们试着跑一下，结果是不是还挺好的~

此时我忽然想到了递归的性质，这个k会不会遍历到右子树的时候回去啊——

果然！他在遍历左子树时问题不大，在遍历右子树时露出了马脚！

所以递归时函数参数的数值变化是个硬伤问题，我们可能需要参考全局变量去解它~

第二种修正方法，增加了全局变量 i，并且移除了k的自减效果，是两个参数都不会受到递归栈的影响。结合以上两个遍历错误，最终的结果是这样的：

⌨️解题代码1（递归，正确解法+错误解法）

#include <iostream>  
#include <queue>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}// 错误解法1
int pre_order_kth1(BiTNode* root, int k) {if (root != nullptr) {cout << "节点数据: " << root->data << " ";cout << "k值: " << k << endl;if (k == 1) {return root->data;}pre_order_kth1(root->lchild, k - 1);pre_order_kth1(root->rchild, k - 1);}
}// 错误解法2
int pre_order_kth2(BiTNode* root, int k) {if (root == nullptr) {return -1; }cout << "节点数据: " << root->data << " ";cout << "k值: " << k << endl;if (k == 1) {return root->data; }--k;int leftResult = pre_order_kth2(root->lchild, k); // 先递归左子树  if (leftResult != -1) {return leftResult;                           // 如果在左子树中找到了，就直接返回结果  }int rightResult = pre_order_kth2(root->rchild, k); // 如果左子树中没有找到，继续递归右子树  if (rightResult != -1) {return rightResult;                           // 如果在右子树中找到了，就直接返回结果  }
}// 正确解法1
static int i = 0;  // 这个静态变量将在所有递归调用中共享和更新  int pre_order_kth3(BiTNode* root, int k) {  // 注意，我们移除了i作为参数  if (root == nullptr) {return -1;}i++;  // 增加全局计数器  cout << "节点数据: " << root->data << " ";cout << "i值: " << i << " ";cout << "k值: " << k << endl;if (k == i) {return root->data;}int left_result = pre_order_kth3(root->lchild, k);  // 不再传递i  if (left_result != -1) {return left_result;}int right_result = pre_order_kth3(root->rchild, k);  // 不再传递i  if (right_result != -1) {return right_result;}return -1;  // 如果没有找到第k个节点，返回-1  
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;int k = 5; int result = -1;result = pre_order_kth1(root1, k);cout << "错误解法1，第" << k << "个节点的数据为：" << result << endl;cout << "——手动分割线——" << endl << endl;result = pre_order_kth2(root1, k);cout << "错误解法2，第" << k << "个节点的数据为：" << result << endl;cout << "——手动分割线——" << endl << endl;result = pre_order_kth3(root1, k);cout << "正确解法1，第" << k << "个节点的数据为：" << result << endl;cout << "——手动分割线——" << endl << endl;return 0;
}

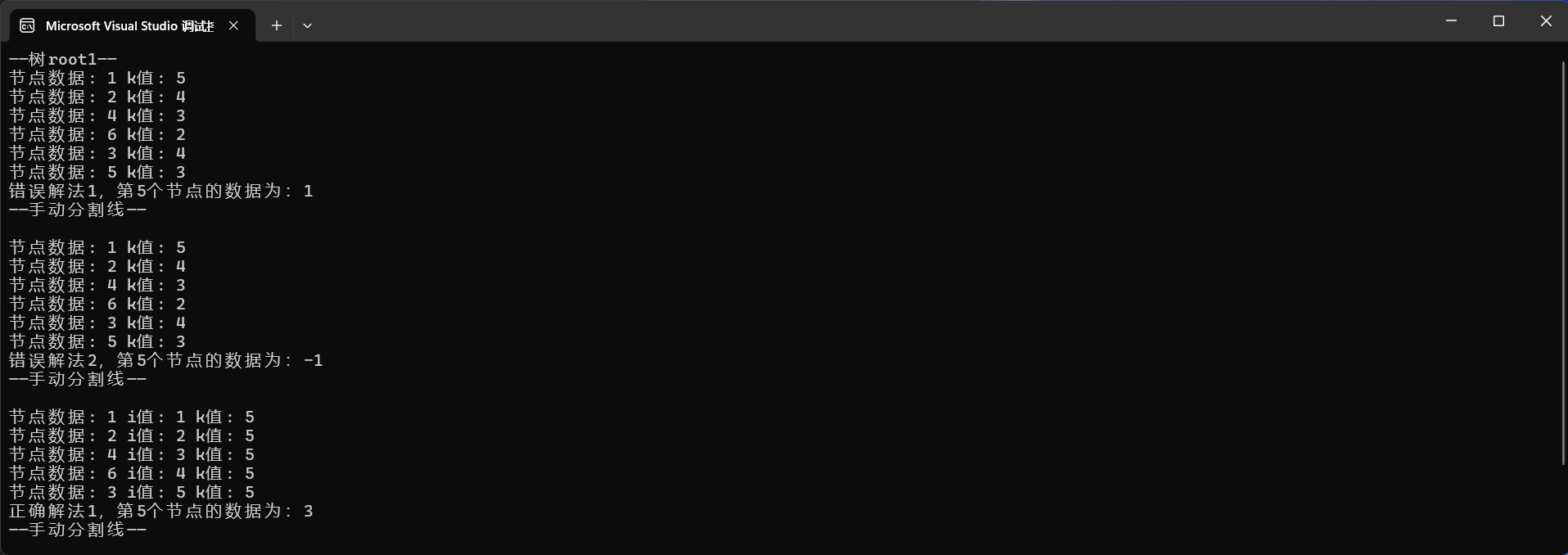
2）非递归算法，没有小坑🕳，在基本的遍历算法基础上，减少k值用于寻找节点就可以了~

⌨️解题代码2（非递归）

int pre_order_kth(BiTNode* root, int k) {if (root == nullptr) {return -1; }stack<BiTNode*> st;BiTNode* node = root;st.push(node);while (st.empty() != true) {node = st.top();st.pop();if (node != nullptr) {cout << "节点数据: " << node->data << " ";cout << "k值: " << k << endl;k--;if (k == 0) {return node->data;}st.push(node->rchild);st.push(node->lchild);}}
}

🧵10 删除子树

🧩题目

已知二叉树以二叉链表存储，编写算法完成:对于树中每个元素值为x的结点，删除以它为根的子树，并释放相应的空间。

📇解题思路

这道题目分为两个部分：寻找节点和删除节点。

首先，我们展示一段（据我肉眼观察，可能是）错误的代码：

bool delete_subtree(BiTNode*& root, int x) {if (root == nullptr) {return false;}// 如果当前节点是目标值，则删除整个子树，并返回true  if (root->data == x) {               delete_subtree(root->lchild, x);		// 递归删除左子树  delete_subtree(root->rchild, x);		// 递归删除右子树  delete root;                          // 删除当前节点  root = nullptr;                       // 将根指针设为nullptr  return true;}// 递归地在左子树和右子树中查找并删除目标节点  bool found_in_left = delete_subtree(root->lchild, x);bool found_in_right = delete_subtree(root->rchild, x);// 如果在左子树或右子树中找到了目标节点，则返回true  return found_in_left || found_in_right;
}

这段代码的查找功能是没有问题的，但是在删除的过程中，仅会切断x值所属的子树与主树的链接，好像不会递归删除左子树和右子树的所有节点，因为root->data == x这个判定条件在x的子树节点不会成立。

所以为了功能看着更清晰不会混淆，这里使用2个函数完成功能~

⌨️解题代码（递归）

#include <iostream>  
#include <queue>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}错误解答1
//bool delete_subtree1(BiTNode*& root, int x) {
//    if (root == nullptr) {
//        return false;
//    }
//
//    // 如果当前节点是目标值，则删除整个子树，并返回true  
//    if (root->data == x) {               
//        delete_subtree1(root->lchild, x);		// 递归删除左子树  
//        delete_subtree1(root->rchild, x);		// 递归删除右子树  
//        delete root;                          // 删除当前节点  
//        root = nullptr;                       // 将根指针设为nullptr  
//        return true;
//    }
//
//    // 递归地在左子树和右子树中查找并删除目标节点  
//    bool found_in_left = delete_subtree1(root->lchild, x);
//    bool found_in_right = delete_subtree1(root->rchild, x);
//
//    // 如果在左子树或右子树中找到了目标节点，则返回true  
//    return found_in_left || found_in_right;
//}void delete_node2(BiTNode*& root) {if (root != nullptr) {delete_node2(root->lchild);delete_node2(root->rchild);delete root;root = nullptr;}
}bool delete_subtree2(BiTNode*& root, int x) {if (root == nullptr) {return false;}if (root->data == x) {delete_node2(root); root = nullptr;return true; }// 如果当前节点不是要删除的节点，则在左右子树中继续查找  bool find_in_left = delete_subtree2(root->lchild, x);if (find_in_left) {return true; // 在左子树中找到了并删除了节点x，返回true  }bool find_in_right = delete_subtree2(root->rchild, x);return find_in_right; // 在右子树中查找并可能删除节点x，返回结果  
}void level_order(BiTNode* root) {if (root == nullptr) return;queue<BiTNode*> qu;qu.push(root);while (!qu.empty()) {BiTNode* node = qu.front();qu.pop();cout << node->data << " ";if (node->lchild != nullptr) {qu.push(node->lchild);}if (node->rchild != nullptr) {qu.push(node->rchild);}}
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;int target1 = 2;cout << "删除以前树的遍历结果为："; level_order(root1);cout << endl;//delete_subtree1(root1, target1);delete_subtree2(root1, target1);cout << "删除以后树的遍历结果为："; level_order(root1);cout << endl << "——手动分割线——"  << endl;return 0;
}

🧵11 寻找祖先节点

🧩题目

在二叉树中查找值为x的结点，试编写算法(用C语言)打印值为x的结点的所有祖先，假设值为x的结点不多于一个。

📇解题思路

这道题目可以使用两种解法：先序遍历+辅助容器或后序遍历+栈。

1）先序遍历+容器的基本思想：一边遍历，一边使用容器记录路径的每一个节点，直到找到x节点的时候，返回记录路径祖先节点的容器。这个方法可能空间开销很大，能够运行，但是不推荐；

2）后序遍历+栈的基本思想：从顶到底遍历，从底到顶输出，找到x节点以后，继续向根节点遍历，记录路径上出现的每一个根节点，这也是王道推荐的解法。后序遍历可能理解有点困难，在本博文的第3题有介绍~~

⌨️解题代码（先序遍历+容器，不推荐）

#include <iostream>  
#include <list>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}bool find_ancestor(BiTNode*& root, int x, list<int>& path) {if (root == nullptr) {return false;}path.push_back(root->data);if (root->data == x) {return true;}if (find_ancestor(root->lchild, x, path) || find_ancestor(root->rchild, x, path)) {return true;}path.pop_back();return false;
}void print_path(const list<int> path) {for (auto it = path.begin(); it != path.end(); it++) {cout << *it << " ";}
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;int target1 = 6;list<int> path;find_ancestor(root1, target1, path);cout << "节点" << target1 << "的祖先节点为：";print_path(path);cout << endl << "——手动分割线——"  << endl;return 0;
}

⌨️解题代码（后序遍历+栈）

#include <iostream>  
#include <stack>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}bool find_ancestor(BiTNode*& root, int x) {if (root == nullptr) {return false;}stack<BiTNode*> st;BiTNode* p = root;    // 用于记录上一次访问的节点  BiTNode* r = nullptr; // 用于记录右子节点cout <<  "后序遍历：" ;while (p != nullptr || !st.empty()) {   // 当前节点不为空或者栈不为空if (p != nullptr) {                 // 当前节点不为空if( p->data == x) {             // 找到目标节点cout << "找到目标节点" << x << endl;while(!st.empty()) {        // 输出栈中元素cout << st.top()->data << " ";st.pop();}return true;}st.push(p);                     // 当前节点入栈p = p->lchild;				    // 访问左子节点}else {p = st.top();                                   // 获取栈顶元素if (p->rchild != nullptr && p->rchild != r) {   // 右子节点存在且未被访问p = p->rchild;      	    // 访问右子节点} else {st.pop();                   // 弹出栈顶元素r = p;  			        // 记录上一次访问的节点p = nullptr;			    // 当前节点置空}}}return false;
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;int target1 = 6;find_ancestor(root1, target1);cout << endl << "——手动分割线——"  << endl;return 0;
}

🧵12 寻找公共祖先节点

🧩题目

设一棵二又树的结点结构为(LLINK,INFO,RLINK)，ROOT 为指向该二又树根结点的指针，p 和 q 分别为指向该二又树中任意两个结点的指针，试编写算法 ANCESTOR(ROOT, p, q, r)，找到p和q的最近公共祖先结点。

📇解题思路

这道题目可以延续11题的两种解法：先序遍历+辅助容器或后序遍历+栈。在本题中，后者的优势会体现得更为明显一些，用一个辅助栈回溯+一个记录节点的FLAG可以就搞定了~

⌨️解题代码（先序遍历+辅助容器，不推荐）

#include <iostream>  
#include <list>
using namespace std;typedef struct BiTNode {int info;BiTNode* llink, * rlink;BiTNode() : info(0), llink(nullptr), rlink(nullptr) {}BiTNode(int x) : info(x), llink(nullptr), rlink(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->llink = new BiTNode(2);root->rlink = new BiTNode(3);root->llink->llink = new BiTNode(4);root->llink->rlink = new BiTNode(5);root->rlink->llink = new BiTNode(6);root->rlink->rlink = new BiTNode(7);return root;
}bool find_ancestor(BiTNode*& root, int data, list<int>& path) {if (root == nullptr) {return false;}path.push_back(root->info);if (root->info == data) {return true;}if (find_ancestor(root->llink, data, path) || find_ancestor(root->rlink, data, path)) {return true;}path.pop_back();return false;
}bool ancestor(BiTNode*& root, int p, int q, int r) {list<int> path1;list<int> path2;if (find_ancestor(root, p, path1) && find_ancestor(root, q, path2)) {cout << "节点" << p << "的祖先节点为：";for (auto it = path1.begin(); it != path1.end(); it++) {cout << *it << " ";}cout << endl;cout << "节点" << q << "的祖先节点为：";for (auto it = path2.begin(); it != path2.end(); it++) {cout << *it << " ";}cout << endl;cout << "节点" << p << "和节点" << q << "的最近公共祖先为：";for (auto it1 = path1.begin(), it2 = path2.begin(); it1 != path1.end() && it2 != path2.end(); it1++, it2++) {if (*it1 == *it2) {r = *it1;}}cout << r << endl;return true;}else {cout << "未找到节点" << p << "或节点" << q << endl;}return false;
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;int target1 = 6;int target2 = 7;int common_root = 1;ancestor(root1, target1, target2, common_root);cout << "——手动分割线——" << endl;return 0;
}

⌨️解题代码（后序遍历+栈）

#include <iostream>  
#include <stack>  
using namespace std;typedef struct bitnode {int info;bitnode* llink, * rlink;bitnode() : info(0), llink(nullptr), rlink(nullptr) {}bitnode(int x) : info(x), llink(nullptr), rlink(nullptr) {}
};bitnode* create_tree1() {bitnode* root = new bitnode(1);root->llink = new bitnode(2);root->rlink = new bitnode(3);root->llink->rlink = new bitnode(4);root->rlink->rlink = new bitnode(5);root->llink->rlink->llink = new bitnode(6);root->rlink->rlink = new bitnode(7);return root;
}bool ancestor(bitnode*& root, int p, int q, int r) {if (root == nullptr) {return false;}stack<bitnode*> st;bitnode* current = root;    // 用于记录上一次访问的节点  bitnode* rail = nullptr;    // 用于记录右子节点int flag = 0;cout <<  "后序遍历：" << endl;while (current != nullptr || !st.empty()) {    // 当前节点不为空或者栈不为空if (current != nullptr) {                  // 当前节点不为空if(current->info == p || current->info == q) {              // 找到目标节点cout << "找到目标节点" << current->info << endl;flag++;if (flag == 2){r = st.top()->info;cout << "节点" << p << "和节点" << q << "的最近公共祖先为：" << r << endl;cout << "路径为：";while(!st.empty()) {           // 输出栈中元素cout << st.top()->info << " ";st.pop();}cout << endl;return true;}}st.push(current);                      // 当前节点入栈current = current->llink;			     // 访问左子节点}else {current = st.top();                    // 获取栈顶元素if (current->rlink != nullptr && current->rlink != rail) {   // 右子节点存在且未被访问current = current->rlink;      	 // 访问右子节点} else {st.pop();                          // 弹出栈顶元素rail = current;  			         // 记录上一次访问的节点current = nullptr;			     // 当前节点置空}}}cout << "未找到目标节点" << endl;return false;
}int main() {bitnode* root1 = create_tree1();cout << "——树root1——" << endl;int target1 = 6;int target2 = 7;int common_root = 1;ancestor(root1, target1, target2, common_root);cout << "——手动分割线——"  << endl;return 0;
}

🧵13 求非空二叉树的宽度

🧩题目

假设二叉树采用二叉链表存储结构，设计一个算法，求非空二又树b的宽度(即具有结
点数最多的那一层的结点个数)。

📇解题思路

这道题目明显适用于层次遍历，和第5题的算法几乎是一模一样的（捡起来改吧改吧就能用），加一个循环记录队列每一层的二叉树节点数量，然后取其中最大的宽度作为返回答案~

⌨️解题代码

#include <iostream>  
#include <queue>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}int width(BiTNode*& root) {if (root == nullptr) {return 0;}int size = 0;int max_size = INT_MIN;cout << "层序遍历：" << endl;queue<BiTNode*> qu;qu.push(root);while (!qu.empty()) {size = qu.size();max_size = max(max_size, size);for(int i = 0; i < size; i++){BiTNode* node = qu.front();qu.pop();cout << node->data << " ";if (node->lchild != nullptr) {qu.push(node->lchild);}if (node->rchild != nullptr) {qu.push(node->rchild);}}}cout << endl << "树的最大宽度为：" << max_size << endl;return max_size;
}int main() {BiTNode* root1 = create_tree1();cout << "——树root1——" << endl;width(root1);cout << endl << "——手动分割线——"  << endl;return 0;
}

🧵14 已知先序求后序

🧩题目

设有一棵满二叉树(所有结点值均不同)，已知其先序序列为 pre，设计一个算法求其后序序列 post。

📇解题思路

😑为了避开写我最讨厌的递归，我还曾经想用数学找规律的方法解这道题目，比如按照固定间隔调换字母顺序什么的，结果发现一点用也没有。适用于第一棵树的不一定也适用于第二棵树，适用于第二棵树的不一定适用第三棵树，囧——

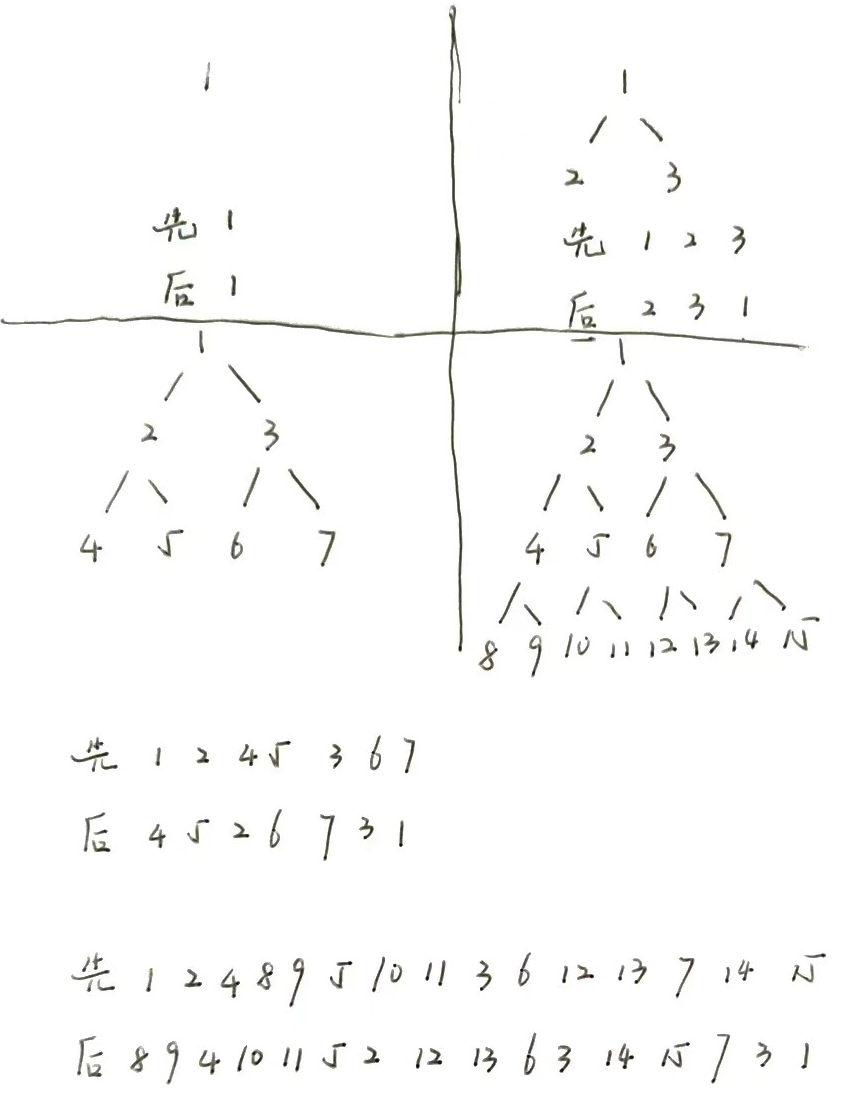
但是我们也能从中间发现一些其它的规律，例如：

第一棵树，后序遍历的起始节点是其本身；

第二棵树，后序遍历的起始节点2位于先序遍历的中间位置，而后+1是右兄弟，再+1是根节点；

第三棵树，后序遍历的起始节点4位于2和5之间，2是1的孩子节点，序号为0+1；5是先序遍历的中间节点，序号为(0+6)/2=3。

第四棵树，后序遍历的起始节点8位于4和9之间，4是2的孩子节点，序号为0+1+1，9是先序遍历的中间节点，需要为(0+14)/2=7——

🤨这好像就是递归的标准写法，先使用二分法找到首节点（子树的左孩子位置），+1是兄弟节点，再回退是根节点~

（但是我还是觉得这道题目很难，其实我也有很多想不懂的点...可能对于递归的原理还是不太了解...）

⌨️解题代码

// 克服了我最最讨厌了递归，我都想夸夸我自己！！#include <iostream>  
#include <vector>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);return root;
}BiTNode* create_tree2() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);return root;
}BiTNode* create_tree3() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->lchild->rchild = new BiTNode(5);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}BiTNode* create_tree4() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->lchild->rchild = new BiTNode(5);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);root->lchild->lchild->lchild = new BiTNode(8);root->lchild->lchild->rchild = new BiTNode(9);root->lchild->rchild->lchild = new BiTNode(10);root->lchild->rchild->rchild = new BiTNode(11);root->rchild->lchild->lchild = new BiTNode(12);root->rchild->lchild->rchild = new BiTNode(13);root->rchild->rchild->lchild = new BiTNode(14);root->rchild->rchild->rchild = new BiTNode(15);return root;
}void pre_order(BiTNode* root, vector<BiTNode*>& pre) {if (root != nullptr) {pre.push_back(root);pre_order(root->lchild, pre);pre_order(root->rchild, pre);}
}void pre_to_post_recursive(vector<BiTNode*>& pre, vector<BiTNode*>& post, int begin, int end) {if (begin < end) {int half = ( begin + end ) / 2;                                // 计算子树大小cout << "begin：" << begin << " " << "end：" << end << " " << "half：" << half << endl;pre_to_post_recursive(pre, post, begin + 1, half);             // 遍历左子树pre_to_post_recursive(pre, post, half + 1, end);               // 遍历右子树}cout << "begin：" << begin << " " << "end：" << end << " " << "pre[begin]：" << pre[begin]->data  << endl;post.push_back(pre[begin]);                                        // 退回根节点
}vector<BiTNode*> pre_to_post(vector<BiTNode*>& pre) {vector<BiTNode*> post;pre_to_post_recursive(pre, post, 0, pre.size() - 1);// 输出后序遍历结果  cout << "满二叉树的后序遍历：";for (BiTNode* node : post) {cout << node->data << " ";}cout << endl;return post;
}int main() {BiTNode* root1 = create_tree1();vector<BiTNode*> pre1;pre_order(root1, pre1);cout << "满二叉树的先序遍历：";for (int i = 0; i < pre1.size(); i++) {cout << pre1[i]->data << " ";}cout << endl;pre_to_post(pre1);cout << "——手动分割线——" << endl << endl;BiTNode* root2 = create_tree2();vector<BiTNode*> pre2;pre_order(root2, pre2);cout << "满二叉树的先序遍历：";for (int i = 0; i < pre2.size(); i++) {cout << pre2[i]->data << " ";}cout << endl;pre_to_post(pre2);cout << "——手动分割线——" << endl << endl;BiTNode* root3 = create_tree3();vector<BiTNode*> pre3;pre_order(root3, pre3);cout << "满二叉树的先序遍历：";for (int i = 0; i < pre3.size(); i++) {cout << pre3[i]->data << " ";}cout << endl;pre_to_post(pre3);cout << "——手动分割线——" << endl << endl;BiTNode* root4 = create_tree4();vector<BiTNode*> pre4;pre_order(root4, pre4);cout << "满二叉树的先序遍历：";for (int i = 0; i < pre4.size(); i++) {cout << pre4[i]->data << " ";}cout << endl;pre_to_post(pre4);cout << "——手动分割线——" << endl << endl;return 0;
}

这里也打印了详细的递归过程，供小伙伴或者以后的我自己参考~

以“begin：0 end：6 half：3”这个格式写的，是递进的过程；

以“begin：2 end：2 pre[begin]：4”这个格式写的，是回归的过程。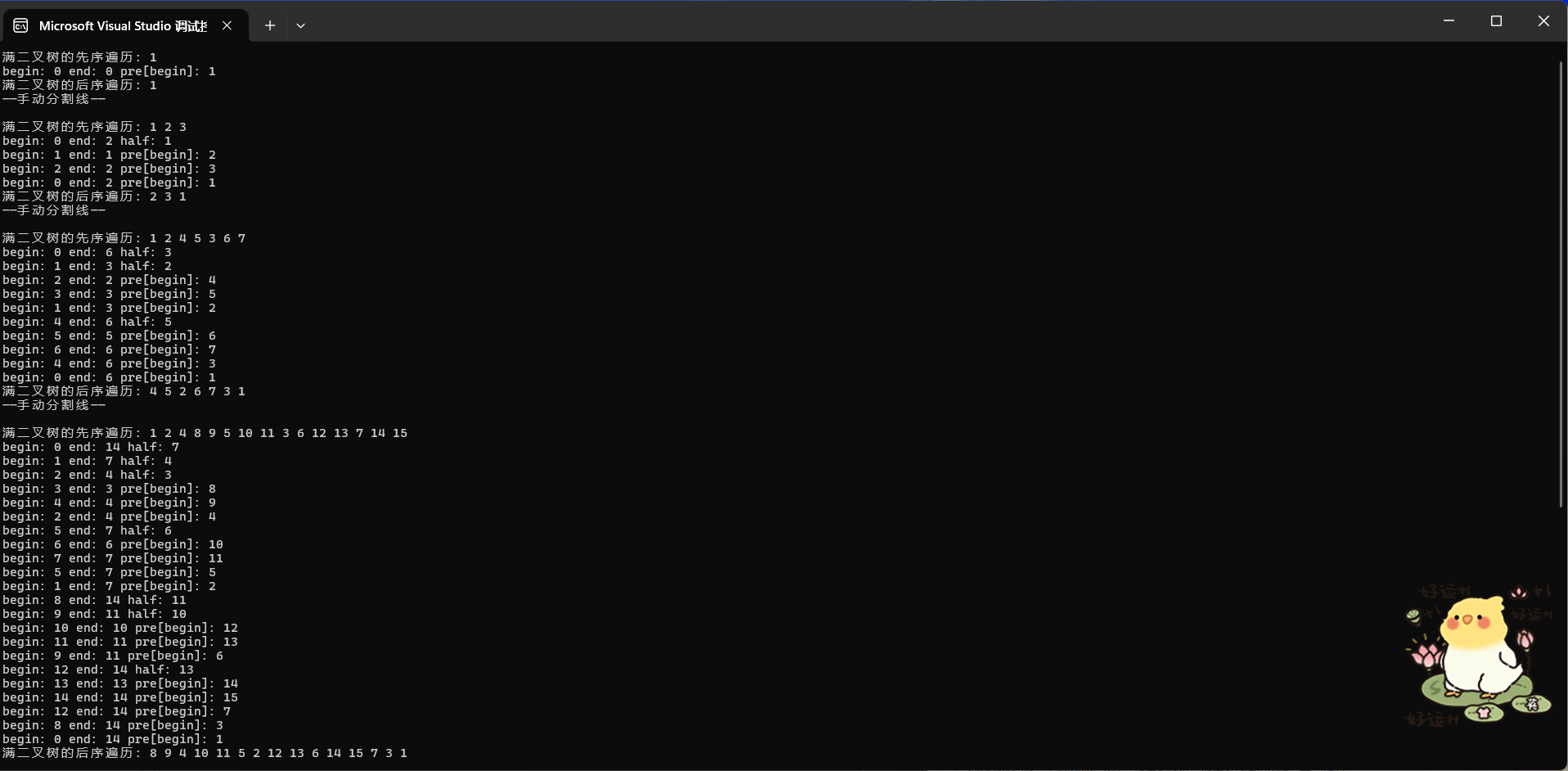

🧵15 串联叶节点

🧩题目

设计一个算法将二叉树的叶结点按从左到右的顺序连成一个单链表，表头指针为 head.
二叉树按二叉链表方式存储，链接时用叶结点的右指针域来存放单链表指针。

📇解题思路

按照惯例，首先祭出一个错误答案。看到题目的时候，我先想到的是层次遍历，因为在我的印象中，叶节点一般就是会在靠近最后一层或者倒数第二层的位置，只要判定好这是个叶节点，然后串起来就可以啦，代码是这样的：

// 失败了，层次遍历会从上往下串叶子结点
BiTNode* create_link(BiTNode* root) {if (root == nullptr) return nullptr;queue<BiTNode*> qu;qu.push(root);BiTNode* head = new BiTNode();BiTNode* leaf_node = head;while (qu.empty() != true) {BiTNode* node = qu.front();qu.pop();if (node->lchild != nullptr) qu.push(node->lchild);if (node->rchild != nullptr) qu.push(node->rchild);if (node->lchild == nullptr && node->rchild == nullptr) {leaf_node->rchild = node;leaf_node = leaf_node->rchild;}}return head;
}

执行的结果确实也是个链表，不过这个链表怎么怪怪的嘞。题目要求从左到右串联，但是小数1号和4号叶节点的位置明显是和题目要求是相反的。大概因为层序遍历会稳定先遍历倒数第二行，再遍历倒数第一行吧~

除了层序遍历以外，还符合从左到右遍历顺序的，那就是中序遍历啦~

⌨️解题代码

#include <iostream>  
#include <queue>  
#include <vector> 
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}BiTNode* create_tree2() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->lchild->rchild = new BiTNode(5);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}BiTNode* create_tree3() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}BiTNode* create_tree4() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);return root;
}失败了，层次遍历会从上往下串叶子结点
//BiTNode* create_link(BiTNode* root) {
//    if (root == nullptr) return nullptr;
//
//    queue<BiTNode*> qu;
//    qu.push(root);
//
//    BiTNode* head = new BiTNode();
//    BiTNode* leaf_node = head;
//
//    while (qu.empty() != true) {
//        BiTNode* node = qu.front();
//        qu.pop();
//
//        if (node->lchild != nullptr) qu.push(node->lchild);
//        if (node->rchild != nullptr) qu.push(node->rchild);
//        if (node->lchild == nullptr && node->rchild == nullptr) {
//            leaf_node->rchild = node;
//            leaf_node = leaf_node->rchild;
//        }
//    }
//
//    return head;
//}void link(BiTNode*& node, BiTNode*& leaf_node) {if (node == nullptr) return;if (node->lchild == nullptr && node->rchild == nullptr) {leaf_node->rchild = node;leaf_node = leaf_node->rchild;}else {link(node->lchild, leaf_node);link(node->rchild, leaf_node);}
}BiTNode* create_link(BiTNode* root) {if (root == nullptr) return nullptr;BiTNode* head = new BiTNode();BiTNode* leaf_node = head;link(root, leaf_node);return head;
}int main() {// 定义一个函数指针数组，存储所有创建树的函数  BiTNode* (*create_tree_funcs[])() = { create_tree1, create_tree2, create_tree3, create_tree4 };const int num_trees = sizeof(create_tree_funcs) / sizeof(create_tree_funcs[0]);// 循环创建树并打印叶子节点  for (int i = 0; i < num_trees; ++i) {BiTNode* root = create_tree_funcs[i]();BiTNode* head = create_link(root);BiTNode* p = head->rchild;cout << "叶子节点链表" << (i + 1) << "：";while (p != nullptr) {cout << p->data << " ";p = p->rchild;}cout << endl;}return 0;
}

🧵16 判断二叉树相似

🧩题目

试设计判断两棵二叉树是否相似的算法。所谓二又树T1和T2相似，指的是T1和T2都是空的二又树或都只有一个根结点；或者T1的左子树和T2的左子树是相似的，且T1的右
子树和 T2的右子树是相似的。

📇解题思路

写个简单的算法同时遍历两棵二叉树就可以解决问题了~

⌨️解题代码

#include <iostream>  
using namespace std;typedef struct BiTNode {int data;BiTNode* lchild, * rchild;BiTNode() : data(0), lchild(nullptr), rchild(nullptr) {}BiTNode(int x) : data(x), lchild(nullptr), rchild(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->rchild = new BiTNode(4);root->rchild->rchild = new BiTNode(5);root->lchild->rchild->lchild = new BiTNode(6);return root;
}BiTNode* create_tree2() {BiTNode* root = new BiTNode(1);root->lchild = new BiTNode(2);root->rchild = new BiTNode(3);root->lchild->lchild = new BiTNode(4);root->lchild->rchild = new BiTNode(5);root->rchild->lchild = new BiTNode(6);root->rchild->rchild = new BiTNode(7);return root;
}BiTNode* create_tree3() {BiTNode* root = new BiTNode(8);root->lchild = new BiTNode(9);root->rchild = new BiTNode(10);root->lchild->lchild = new BiTNode(11);root->lchild->rchild = new BiTNode(12);root->rchild->lchild = new BiTNode(13);root->rchild->rchild = new BiTNode(14);return root;
}bool is_similar(BiTNode* root1, BiTNode* root2) {if (root1 == nullptr && root2 == nullptr) return true;if (root1 == nullptr || root2 == nullptr) return false;return is_similar(root1->lchild, root2->lchild) && is_similar(root1->rchild, root2->rchild);
}int main() {BiTNode* root1 = create_tree1();BiTNode* root2 = create_tree2();BiTNode* root3 = create_tree3();cout << "root1, root2是否相似：" << is_similar(root1, root2) << endl;cout << "root2, root3是否相似：" << is_similar(root2, root3) << endl;return 0;
}

🧵17 二叉树带权路径长度

🧩题目

【2014 统考真题】二叉树的带权路径长度(WPL)是二又树中所有叶结点的带权路径长度之和。给定一棵二叉树 T，采用二叉链表存储，结点结构为

left weight right

其中叶结点的 weight 域保存该结点的非负权值。设 root 为指向T的根结点的指针,请设计求T的 WPL的算法，要求:
1)给出算法的基本设计思想。
2)使用C或C++语言，给出二叉树结点的数据类型定义。
3)根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

📇解题思路

这个考点好像是类似哈夫曼树的算法，在求树深度的代码基础上，增加权值计算就可以了~

🌸数据结构05：树与二叉树[C++][哈夫曼树HuffmanTree]

⌨️解题代码

#include <iostream>  
#include <queue>  
#include <vector> 
using namespace std;typedef struct BiTNode {int weight;BiTNode* left, * right;BiTNode() : weight(0), left(nullptr), right(nullptr) {}BiTNode(int x) : weight(x), left(nullptr), right(nullptr) {}
};BiTNode* create_tree() {BiTNode* root = new BiTNode(1);root->left = new BiTNode(2);root->right = new BiTNode(3);root->left->right = new BiTNode(4);root->right->right = new BiTNode(5);root->left->right->left = new BiTNode(6);return root;
}int count_wpl(BiTNode* root, int depth){if (root == nullptr) return 0;if (root->left == nullptr && root->right == nullptr) return root->weight * depth;return count_wpl(root->left, depth + 1) + count_wpl(root->right, depth + 1);
}int wpl(BiTNode* root) {int depth = 0;return count_wpl(root, depth);
}int main() {BiTNode* root = create_tree();int result = wpl(root);cout << "WPL: " << result << endl;return 0;
}

🧵18 二叉树带权路径长度

🧩题目

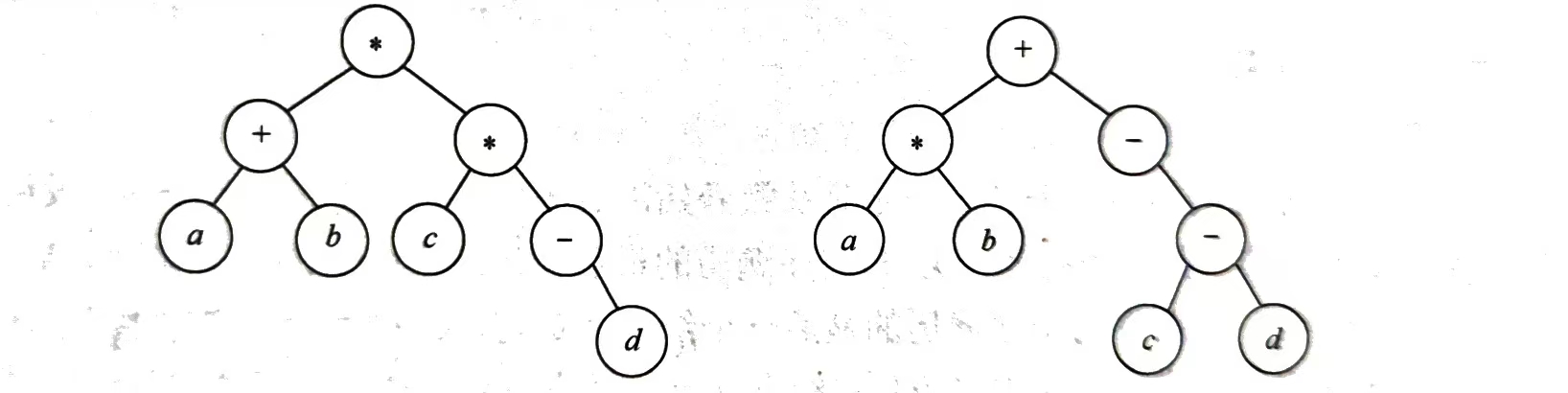
【2017统考真题】请设计一个算法，将给定的表达式树(二叉树)转换为等价的中缀表达式(通过括号反映操作符的计算次序)并输出。例如，当下列两棵表达式树作为算法的输入时：

输出的等价中缀表达式分别为(a+b)*(c*(-d))和(a*b)+(-(c-d))。二叉树结点定义如下:
typedef struct node(
char data[10]; //存储操作数或操作符
struct node *left，*right;
}BTree;
要求:
1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

📇解题思路1

这道题目是中序遍历无疑，难就难括号的处理。

第一种思路，是按照节点的内容与树中的位置结合起来考虑，目前看来，只有没有左子树的字母和只有右子树的“-”需要“(”，没有右子树的字母需要“)”。

但是有一个问题，像a和b这种字母，都是既没有左子树又没有右子树，满足加左右括号的判定条件，怎么能保证它不变成这样呢(a)+(b)？

这一点，我们增加了一个判断的变量left，当left == 1时，表示正在访问左节点，当left == 0时，表示正在访问右节点~

按照这个思路完成的代码如下——

⌨️解题代码1（繁琐，不推荐）

#include <iostream>  
#include <vector>
#include <cctype>
using namespace std;typedef struct BiTNode {char data;BiTNode* left, * right;BiTNode() : data(0), left(nullptr), right(nullptr) {}BiTNode(char x) : data(x), left(nullptr), right(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode('*');root->left = new BiTNode('+');root->right = new BiTNode('*');root->left->left = new BiTNode('a');root->left->right = new BiTNode('b');root->right->left = new BiTNode('c');root->right->right = new BiTNode('-');root->right->right->right = new BiTNode('d');return root;
}BiTNode* create_tree2() {BiTNode* root = new BiTNode('+');root->left = new BiTNode('*');root->right = new BiTNode('-');root->left->left = new BiTNode('a');root->left->right = new BiTNode('b');root->right->right = new BiTNode('-');root->right->right->left = new BiTNode('c');root->right->right->right = new BiTNode('d');return root;
}void in_order(BiTNode* node, vector<char>& result, int left) {if (node != nullptr) {if (isalpha(node->data) && left == 1) {result.push_back('(');}if (node->data == '-' && node->left == nullptr && node->right != nullptr) {result.push_back('(');}in_order(node->left, result, 1);result.push_back(node->data);in_order(node->right, result, 0);if (node->data == '-' && node->left == nullptr && node->right != nullptr) {result.push_back(')');}if (isalpha(node->data) && left == 0) {result.push_back(')');}}
}vector<char> solution(BiTNode* root) {vector<char> result;bool left = 0;char left_alpha = NULL;in_order(root, result, left);return result;
}int main() {BiTNode* root1 = create_tree1();vector<char> result1 = solution(root1);cout << "树1的遍历结果：";for (auto node : result1) {cout << node << " ";}cout << endl;BiTNode* root2 = create_tree2();vector<char> result2 = solution(root2);cout << "树2的遍历结果：";for (auto node : result2) {cout << node << " ";}cout << endl;return 0;
}

📇解题思路2

第二种思路，优先根据树的深度解题，而无需考虑节点中的内容，这也是王道书中的标准解法。

先遍历左子树，增加左括号“("，然后完成根节点的中序遍历”a+b"，再增加右括号“)”；

同样，在遍历右子树时，增加左括号“("，然后完成根节点的中序遍历”c*"，再遍历右子树“(-d)，最后增加右括号“)”。

⌨️解题代码2

#include <iostream>  
#include <vector>
#include <cctype>
using namespace std;typedef struct BiTNode {char data;BiTNode* left, * right;BiTNode() : data(0), left(nullptr), right(nullptr) {}BiTNode(char x) : data(x), left(nullptr), right(nullptr) {}
};BiTNode* create_tree1() {BiTNode* root = new BiTNode('*');root->left = new BiTNode('+');root->right = new BiTNode('*');root->left->left = new BiTNode('a');root->left->right = new BiTNode('b');root->right->left = new BiTNode('c');root->right->right = new BiTNode('-');root->right->right->right = new BiTNode('d');return root;
}BiTNode* create_tree2() {BiTNode* root = new BiTNode('+');root->left = new BiTNode('*');root->right = new BiTNode('-');root->left->left = new BiTNode('a');root->left->right = new BiTNode('b');root->right->right = new BiTNode('-');root->right->right->left = new BiTNode('c');root->right->right->right = new BiTNode('d');return root;
}void Btree_To_Exp(BiTNode* root, int deep) {if (root == nullptr) {return;}else if(root->left == nullptr && root->right == nullptr) {cout << root->data;}else {if (deep > 1) {cout << "(";}Btree_To_Exp(root->left, deep + 1);cout << root->data;Btree_To_Exp(root->right, deep + 1);if (deep > 1) {cout << ")";}}
}void Btree_To_E(BiTNode* root) {Btree_To_Exp(root, 1);
}int main() {BiTNode* root1 = create_tree1();cout << "树1的遍历结果：";Btree_To_E(root1);cout << endl;BiTNode* root2 = create_tree2();cout << "树2的遍历结果：";Btree_To_E(root2);cout << endl;return 0;
}

🧵19 判断是否为二叉树搜索树

🧩题目

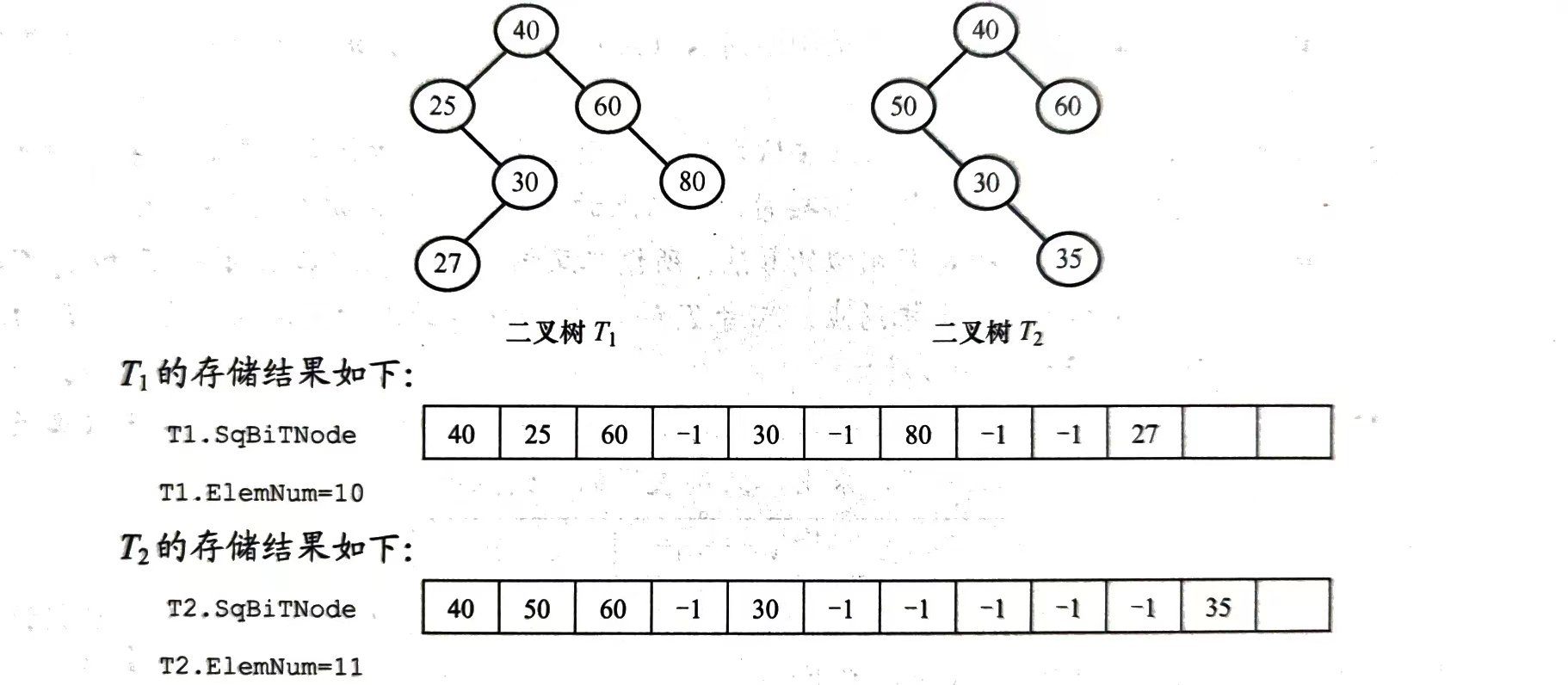
【2022 统考真题】已知非空二叉树T的结点值均为正整数，采用顺序存储方式保存，数据结构定义如下:

typedef struct {                                //MAX SIZE为已定义常量
        int SqBiTNode[MAXSIE];        //保存二叉树结点值的数组

        int ElemNum; //实际占用的数组元素个数
}SqBiTree;

请设计一个尽可能高效的算法，判定一棵采用这种方式存储的二叉树是否为二叉搜索树，若是，则返回 true，否则，返回false。要求:

1)给出算法的基本设计思想。

2)根据设计思想，采用C或 C++语言描述算法，关键之处给出注释。

📇解题思路

这棵树的考点好像是朴素二叉排序树。

🌸数据结构07：查找[C++][朴素二叉排序树BST]-CSDN博客

我们假设它时按照“左子树<根节点<右子树”的规律进行判断，那这个明显就是中序遍历的算法~

但题目的数据结构明显是按照层序遍历存放的...呃，层序就层序吧，层序也能判断，根据数组存放位置，左子树在2i + 1的位置，右子树在2i + 2的位置。反正只要不满足“左子树<根节点<右子树”的规律，他就不是排序二叉树咯~

⌨️解题代码1

#include <iostream>
using namespace std;static const int MAX_SIZE = 12;typedef struct {int SqBiTNode[MAX_SIZE];int ElemNum;
}SqBiTree;bool is_BST(SqBiTree tree, int index, int& num, bool left) {if (index < tree.ElemNum && tree.SqBiTNode[index] != -1) {if (num == -1) {num = tree.SqBiTNode[index];}else {if (tree.SqBiTNode[index] > num && left == true) {return false;}if (tree.SqBiTNode[index] < num && left == false) {return false;}num = tree.SqBiTNode[index];}if (!is_BST(tree, 2 * index + 1, num, 1)) {return false;}if (!is_BST(tree, 2 * index + 2, num, 0)) {return false;}}return true;
}bool is_search_tree(SqBiTree tree) {if (tree.ElemNum == 0) {return false;}int index = 0;int num = tree.SqBiTNode[index];bool left = false;return is_BST(tree, index, num, left);
}int main() {SqBiTree tree1 = { {40, 25, 60, -1, 30, -1, 80, -1, -1, 27}, 10 };SqBiTree tree2 = { {40, 50, 60, -1, -1, -1, -1, -1, -1, 35}, 11 };cout << "树1是否为二叉树：" << is_search_tree(tree1) << endl;cout << "树2是否为二叉树：" << is_search_tree(tree2) << endl;return 0;
}

⌨️解题代码2

另外附王道书的标准答案，我隐隐约约觉得这段代码和我的想法是一样的，但是这段代码写得太简洁了，我就有点绕不明白。看起来好像真的是用层序遍历的数据结构实现中序遍历的算法——

#include <iostream>
using namespace std;static const int MAX_SIZE = 12;typedef struct {int SqBiTNode[MAX_SIZE];int ElemNum;
}SqBiTree;bool judgeInOrderBST(SqBiTree bt, int k, int* val) {if (k < bt.ElemNum && bt.SqBiTNode[k] != -1) {// 先递归检查左子树  if (!judgeInOrderBST(bt, 2 * k + 1, val)) return false;// 检查当前节点值是否大于之前的最大值  if (bt.SqBiTNode[k] <= *val) return false;// 更新当前最大值为当前节点值  *val = bt.SqBiTNode[k];// 再递归检查右子树  if (!judgeInOrderBST(bt, 2 * k + 2, val)) return false;}return true;
}int main() {SqBiTree tree1 = { {40, 25, 60, -1, 30, -1, 80, -1, -1, 27}, 10 };SqBiTree tree2 = { {40, 50, 60, -1, -1, -1, -1, -1, -1, 35}, 11 };int val_tree1 = INT_MIN; // 初始化val为int能表示的最小值  int val_tree2 = INT_MIN; // 初始化val为int能表示的最小值  cout << "树1是否为二叉搜索树：" << judgeInOrderBST(tree1, 0, &val_tree1) << endl;cout << "树2是否为二叉搜索树：" << judgeInOrderBST(tree2, 0, &val_tree2) << endl;return 0;
}

🔚结语

博文到此结束，写得模糊或者有误之处，欢迎小伙伴留言讨论与批评，督促博主优化内容{例如有错误、难理解、不简洁、缺功能}等，博主会顶锅前来修改~😶‍🌫️

我是梅头脑，本片博文若有帮助，欢迎小伙伴动动可爱的小手默默给个赞支持一下，收到点赞的话，博主肝文的动力++~🌟🌟

同系列的博文：🌸数据结构_梅头脑_的博客-CSDN博客

同博主的博文：🌸随笔03 笔记整理-CSDN博客

数据结构05：树与二叉树习题02[C++]

🧵01-02 二叉树的先序序列与后序序列

🧵03 后序遍历二叉树非递归算法

🧵04 二叉树逆向层次遍历

🧵05 非递归算法求二叉树高度

🧵06 判断完全二叉树

🧵07 判断双分支节点个数

🧵08 交换二叉树左右子树

🧵09 先序遍历第k个节点的值

🧵10 删除子树

🧵11 寻找祖先节点

🧵12 寻找公共祖先节点

🧵13 求非空二叉树的宽度

🧵14 已知先序求后序

🧵15 串联叶节点

🧵16 判断二叉树相似

🧵17 二叉树带权路径长度

🧵18 二叉树带权路径长度

🧵19 判断是否为二叉树搜索树

🔚结语

最新新闻

热搜词

数据结构05：树与二叉树 习题02[C++]

🧵01-02 二叉树的先序序列与后序序列

🧵03 后序遍历二叉树非递归算法

🧵04 二叉树逆向层次遍历

🧵05 非递归算法求二叉树高度

🧵06 判断完全二叉树

🧵07 判断双分支节点个数

🧵08 交换二叉树左右子树

🧵09 先序遍历第k个节点的值

🧵10 删除子树

🧵11 寻找祖先节点

🧵12 寻找公共祖先节点

🧵13 求非空二叉树的宽度

🧵14 已知先序求后序

🧵15 串联叶节点

🧵16 判断二叉树相似

🧵17 二叉树带权路径长度

🧵18 二叉树带权路径长度

🧵19 判断是否为二叉树搜索树

🔚结语

最新新闻

热搜词

数据结构05：树与二叉树习题02[C++]