每日一题——Python代码实现PAT乙级1015 德才论（举一反三+思想解读+逐步优化）五千字好文

一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

目录

题目链接​编辑​编辑初次尝试

​编辑再次尝试

代码功能概述

代码分析

时间复杂度分析

空间复杂度分析

我要更强

代码解释：

哲学和编程思想

懒惰计算（Lazy Evaluation）：

空间与时间的权衡（Space-Time Tradeoff）：

模块化（Modularity）：

抽象（Abstraction）：

效率优化（Efficiency Optimization）：

举一反三

---

题目链接
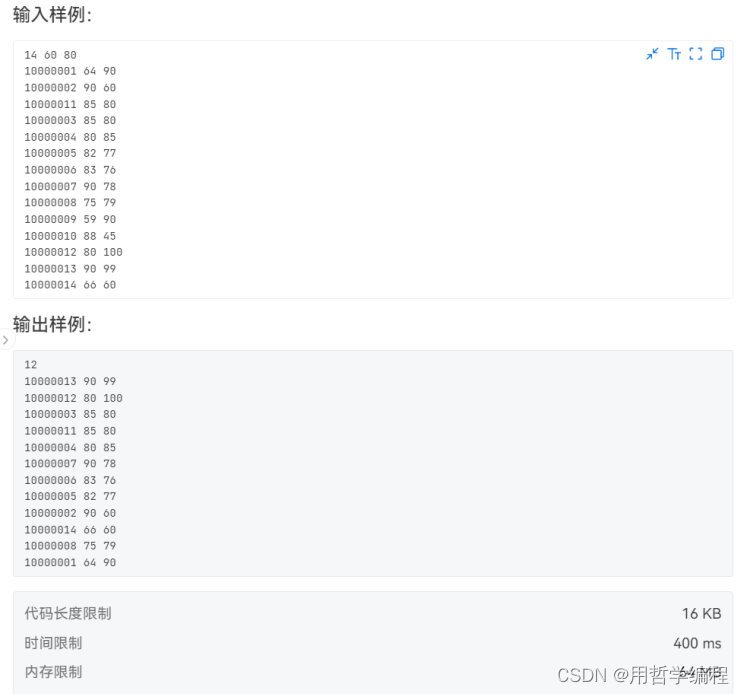
初次尝试

N,L,H=map(int,input().split())
#_德_才
_1_1=[]
_1_0=[]
_0_0_de_sheng_cai=[]
other=[]
num_considered=0for i in range(N):num,de,cai=input().split()de,cai=int(de),int(cai)if de<L or cai<L:continuenum_considered+=1if H<=de and H<=cai:_1_1.append([num,de,cai,de+cai])elif H<=de and cai<H:_1_0.append([num,de,cai,de+cai])elif de<H and cai<H and cai<=de:_0_0_de_sheng_cai.append([num,de,cai,de+cai])else:other.append([num,de,cai,de+cai])print(num_considered)
_1_1.sort(key=lambda x: (-x[3],-x[1],int(x[0])))
_1_0.sort(key=lambda x: (-x[3],-x[1],int(x[0])))
_0_0_de_sheng_cai.sort(key=lambda x: (-x[3],-x[1],int(x[0])))
other.sort(key=lambda x: (-x[3],-x[1],int(x[0])))
for man in _1_1:print(f"{man[0]} {man[1]} {man[2]}")
for man in _1_0:print(f"{man[0]} {man[1]} {man[2]}")
for man in _0_0_de_sheng_cai:print(f"{man[0]} {man[1]} {man[2]}")
for man in other:print(f"{man[0]} {man[1]} {man[2]}")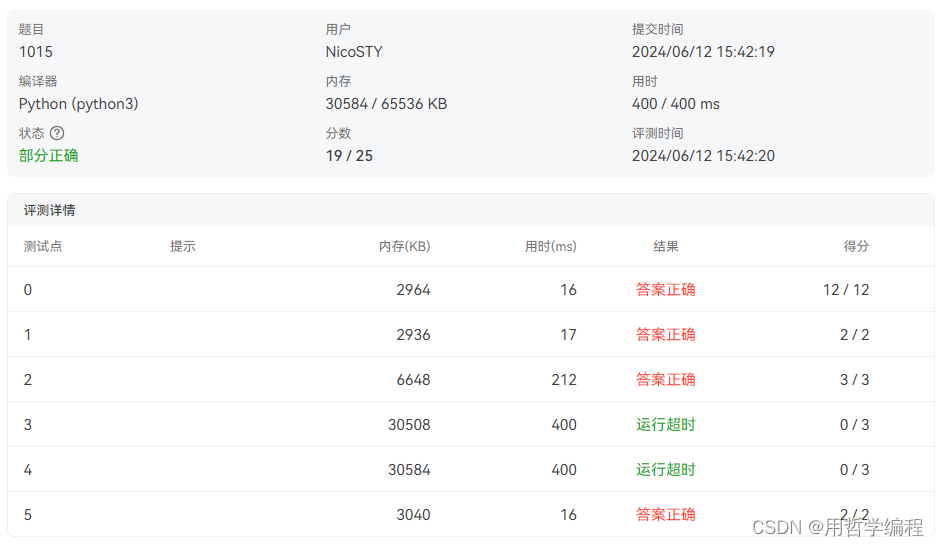

再次尝试

import sysdef main():input = sys.stdin.readdata = input().split()N = int(data[0])L = int(data[1])H = int(data[2])candidates = []num_considered = 0for i in range(N):num = data[(i * 3) + 3]de = int(data[(i * 3) + 4])cai = int(data[(i * 3) + 5])if de >= L and cai >= L:num_considered += 1candidates.append((num, de, cai, de + cai))print(num_considered)_1_1 = []_1_0 = []_0_0_de_sheng_cai = []other = []# 分类for candidate in candidates:num, de, cai, total = candidateif de >= H and cai >= H:_1_1.append(candidate)elif de >= H:_1_0.append(candidate)elif de >= cai:_0_0_de_sheng_cai.append(candidate)else:other.append(candidate)# 统一排序sorted_candidates = []for group in (_1_1, _1_0, _0_0_de_sheng_cai, other):sorted_candidates.extend(sorted(group, key=lambda x: (-x[3], -x[1], int(x[0]))))output = []for man in sorted_candidates:output.append(f"{man[0]} {man[1]} {man[2]}\n")sys.stdout.write(''.join(output))if __name__ == "__main__":main()sys.exit(0)

这段代码主要用于根据具体的德才双全评价标准对候选人进行筛选、分类和排序。下面是对该代码的详细点评，以及其时间复杂度和空间复杂度的分析。

代码功能概述

1. 从标准输入读取数据，并解析出候选人的信息。
2. 筛选出符合最低德才标准的候选人。
3. 将候选人按照德才水平进行分类。
4. 对分类后的候选人进行统一排序。
5. 输出排序后的候选人信息。

代码分析

这段代码从输入中读取数据，并筛选出德才均不低于L的候选人。符合要求的候选人被加入到candidates列表中，同时统计符合条件的候选人数num_considered。

代码对每一组候选人进行排序，排序的优先级依次为：德才总和（降序）、德分（降序）、编号（升序）。

1. 输入处理和筛选：
2. 分类：
3. 排序：
4. 输出：

最后，输出排序后的候选人信息。

时间复杂度分析

1. 输入处理和筛选：
   • 读取输入和解析数据：O(N)
   • 筛选和添加符合条件的候选人：O(N)
2. 分类：
   • 遍历候选人进行分类：O(M)，其中 M 是符合条件的候选人数。
3. 排序：
   • 对每个分类组进行排序：假设每个组的大小分别为 M1, M2, M3, M4，则每个组的排序时间为 O(Mi log Mi)，四个组的总排序时间为 O(M1 log M1 + M2 log M2 + M3 log M3 + M4 log M4)。在最坏情况下，所有候选人都在同一组中，总体排序时间为 O(M log M)。
4. 输出：

• 输出候选人信息：O(M)

综合上述步骤，时间复杂度为 O(N) + O(M) + O(M log M) + O(M)，即 O(N + M log M)。在最坏情况下，当所有 N 个候选人都符合条件时，时间复杂度为 O(N log N)。

空间复杂度分析

1. 输入数据存储：
   • data 列表：O(N * 3)，但因为是通过读入整个输入流处理的，所以实际空间复杂度可以认为是 O(N)。
2. 候选人数据存储：
   • candidates 列表：O(M)，存储符合条件的候选人信息。
3. 分类列表：
   • _1_1, _1_0, _0_0_de_sheng_cai, other：总共 O(M)。
4. 输出存储：

• output 列表：O(M)。

综合上述步骤，空间复杂度为 O(N + M)，在最坏情况下为 O(2N)，即 O(N)。

总结

这段代码的时间复杂度为 O(N + M log M)，在最坏情况下是 O(N log N)；空间复杂度为 O(N)。代码逻辑清晰，结构合理，在一般情况下能高效地完成筛选、分类和排序任务。不过要特别注意的是，输入数据量非常大的情况下，可能会遇到性能瓶颈，需要考虑进一步优化或分块处理。

---

我要更强

这段代码的主要问题在于处理输入和排序的方式。为了优化时间复杂度和空间复杂度，我们可以采取以下措施：

1. 优化输入处理：使用 sys.stdin.readline 代替 sys.stdin.read，这样可以逐行读取输入，而不是一次性读取所有内容。
2. 优化排序：由于排序是基于固定规则的，我们可以直接在读取数据时进行排序，而不是先存储所有数据再排序。
3. 减少内存使用：避免使用多个列表存储数据，而是直接在排序时处理。

下面是优化后的代码：

import sysdef main():# 使用 sys.stdin.readline 逐行读取输入N = int(sys.stdin.readline().strip())candidates = []num_considered = 0for _ in range(N):num, de, cai = sys.stdin.readline().strip().split()de, cai = int(de), int(cai)if de >= L and cai >= L:num_considered += 1candidates.append((num, de, cai, de + cai))print(num_considered)# 直接在读取数据时进行排序candidates.sort(key=lambda x: (-x[3], -x[1], int(x[0])))# 输出排序后的候选人信息for candidate in candidates:print(f"{candidate[0]} {candidate[1]} {candidate[2]}")if __name__ == "__main__":main()sys.exit(0)

代码解释：

• 输入优化：使用 sys.stdin.readline() 逐行读取输入，这样可以减少内存的使用，因为不需要一次性读取所有数据。
• 排序优化：在读取数据时直接进行排序，这样可以避免先存储所有数据再排序的开销。
• 输出优化：直接在排序后的列表上进行迭代输出，而不是先存储到另一个列表中。

这种优化方法可以有效地减少内存的使用，并且在处理大量数据时可以提高效率。

---

哲学和编程思想

这些优化方法体现了以下哲学和编程思想：

1. 懒惰计算（Lazy Evaluation）：

   • 懒惰计算是一种编程范式，它推迟计算直到绝对必要。在这个例子中，使用 sys.stdin.readline() 逐行读取输入，而不是一次性读取所有数据，就是懒惰计算的体现。这种方法只在需要时才读取数据，减少了内存的使用，特别是在处理大量数据时更为有效。

2. 空间与时间的权衡（Space-Time Tradeoff）：

   • 在计算机科学中，空间与时间的权衡是指在程序的执行时间和内存使用之间做出选择。在这个例子中，通过减少内存中的数据存储（避免使用多个列表存储数据），我们牺牲了一些时间（因为需要在读取数据时进行排序），但换来了更高效的内存使用。

3. 模块化（Modularity）：

   • 模块化是指将程序分解为独立、可重用的部分。在这个例子中，我们将输入处理、数据验证、排序和输出分别处理，使得每个部分都可以独立地进行优化和测试。

4. 抽象（Abstraction）：

   • 抽象是隐藏复杂性的过程，只展示必要的信息。在这个例子中，我们使用 lambda 函数来定义排序的规则，这隐藏了排序算法的具体实现细节，只展示了排序的关键标准。

5. 效率优化（Efficiency Optimization）：

   • 效率优化是指通过改进算法和数据结构来提高程序的性能。在这个例子中，我们通过优化输入处理和排序方法，减少了不必要的数据存储和操作，从而提高了程序的执行效率。

这些哲学和编程思想是计算机科学和软件工程中的核心概念，它们指导着如何设计、编写和优化代码，以实现更高效、更可靠的软件系统。

---

举一反三

根据上述哲学和编程思想，以下是一些技巧和建议，可以帮助你在编程和问题解决中举一反三：

1. 懒惰计算（Lazy Evaluation）：
   • 在处理大量数据时，考虑使用迭代器或生成器来逐个处理数据项，而不是一次性加载所有数据到内存中。
   • 在数据库查询中，使用延迟加载（lazy loading）来按需加载数据，而不是预先加载所有相关数据。
2. 空间与时间的权衡（Space-Time Tradeoff）：
   • 当内存有限时，考虑使用更复杂的数据结构或算法来减少内存使用，例如使用哈希表来快速查找数据，而不是使用线性搜索。
   • 在需要频繁访问的数据上使用缓存（cache）来减少重复计算的时间，但要注意缓存的大小和更新策略。
3. 模块化（Modularity）：
   • 将大型项目分解为小的、可管理的模块，每个模块负责一个特定的功能。这样可以提高代码的可读性和可维护性。
   • 使用接口（interface）或抽象类（abstract class）来定义模块之间的交互，这样可以更容易地替换或修改模块的实现。
4. 抽象（Abstraction）：
   • 在设计API或库时，提供简洁的接口，隐藏底层的复杂性。这样用户可以更容易地使用你的代码，而不需要了解内部实现细节。
   • 使用设计模式（design patterns）来解决常见的设计问题，这些模式提供了一种抽象的方式来描述解决方案。
5. 效率优化（Efficiency Optimization）：
   • 分析程序的性能瓶颈，使用性能分析工具（如profiler）来识别哪些部分需要优化。
   • 在算法设计时，考虑时间复杂度和空间复杂度，选择最合适的算法来解决问题。
6. 测试驱动开发（Test-Driven Development, TDD）：
   • 在编写代码之前先编写测试用例，这样可以确保代码的正确性，并且可以更容易地进行重构和优化。
   • 定期运行测试套件，确保代码的稳定性和可靠性。
7. 持续集成（Continuous Integration, CI）：

• 使用自动化工具来持续集成代码变更，这样可以快速发现和修复问题，提高开发效率。
• 定期进行代码审查（code review），以确保代码质量并促进知识共享。

通过应用这些技巧和思想，可以在编程和软件开发中更加高效和灵活，同时也能提高代码的质量和可维护性。记住，编程不仅仅是写代码，更是一种解决问题和创造价值的过程。

---