513.找树左下角的值
用层序遍历很简单,这里讲递归。
怎么判断是最后一行?深度最深的叶子节点就是最后一行 -> 记录一个maxDepth和targetVal,每次遍历到叶子结点就比较currentDepth和maxDepth,targetVal = currnetDepth > maxDepth ? currentVal : targetVal
怎么判断是最左边的?每次递归保证左节点优先处理,这样就能保证左节点最先拿到最大的maxDepth,这样根据上面,就能保证即使遍历到最后一行的其他叶子结点,targetVal也不会被覆盖(因为写的是currnetDepth > maxDepth才会更新targetVal)
遍历顺序用什么?这道题中不需要处理中节点,但是要保证左节点优先于右结点,因此我选择前序遍历
设递归函数为preOrderTravesal(node),作用是前序遍历,没有返回值。
递归三部曲:
- 确认参数
- 入参只有node
- 类的属性有targetVal(记录着当前遍历到的最深的那一层的最左边的那一个值),maxDepth(记录着当前遍历到的最深的深度),currentDepth(记录着当前遍历到的节点的深度)
- 终止条件:
- 如果是叶子节点
if (currentDepth > maxDepth) {maxDepth = currentDepth;targetVal = node.val;
}
targetVal = currnetDepth > maxDepth ? currentVal : targetVal
- 每一层的处理逻辑:
判断是否满足终止条件
if (node.left != null){currentDepth++;preOrderTravesal(node.left)currentDepth--;
}
if (node.right != null){currentDepth++;preOrderTravesal(node.right)currentDepth--;
}我感觉,如果需要遍历一棵树的不同的分支并且处理,同时处理的过程中需要x,同时这个x会随着遍历的深度而改变,那么此时就要用回溯
class Solution {int targetVal;int maxDepth = 0;int currentDepth = 0;public int findBottomLeftValue(TreeNode root) {currentDepth++;preOrderTraversal(root);currentDepth--;return targetVal;}public void preOrderTraversal (TreeNode node) {if (node.right == null && node.left == null) {if (currentDepth > maxDepth) {maxDepth = currentDepth;targetVal = node.val;}}// 中// 左if (node.left != null) {currentDepth++;preOrderTraversal(node.left);currentDepth--;}// 右if (node.right != null){currentDepth++;preOrderTraversal(node.right);currentDepth--;}}
}
112. 路径总和
递归函数什么时候需要返回值?什么时候不需要返回值?这里总结如下三点:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。
我一开始的思路是之前有一道题的探索所有路径,然后看看加起来有没有是目标值的
虽然卡哥说不管哪种遍历顺序都可以,但我只能想通前序遍历,因为我觉得只有知道了root -> currentNode,才能继续分别探索currentNode -> 左右子树的路径
关于判断路径之和是不是目标值,我一开始想的是每次找出一条根节点到叶子结点的路径就累加一下,但是卡哥的思路更加巧妙
首先计数器如何统计这一条路径的和呢?
不要去累加然后判断是否等于目标和,那么代码比较麻烦,可以用递减,让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。
如果最后count == 0,同时到了叶子节点的话,说明找到了目标和。
如果遍历到了叶子节点,count不为0,就是没找到。
这次的递归函数设计为hasTargetPath(node),作用为判断是否有满足要求的路径,有返回值,返回值为这套路径是否满足要求。
类的属性为rest,表示当前距离目标值还要减去多少
此时探索不同路径的时候都需要用到同一个rest,因此需要回溯
那么此时就要找出所有可能产生返回值的情况:
- 如果node是叶子节点,那么就判断
rest - node.val == 0,如果为真,表示找到了,返回true;否则返回false - 如果node不是叶子节点,那么
// 中:减掉当前节点
rest -= node.val
// 左
if (node.left != null) {// 向左探索boolean leftRes = hasTargetPath(node.left); // 在执行这个函数的时候,会执行rest -= node.left,因此下面的回溯要补回来if (leftRes == true) {// 说明左边探索出了一条可以的道路return true;} else {// 说明左侧没有符合要求的路径,此时要把rest恢复成没有向左探索之前的样子,来给右边探索铺路rest += node.left}
}// 右同理
class Solution {int rest;public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) return false;rest = targetSum;return hasTargetPath(root);}boolean hasTargetPath(TreeNode node) {if (node.left == null && node.right == null) {// 即使到了终结条件的节点,也要考虑到后面要回溯// 因此不能写 return rest - node.val == 0,因为这样的话rest其实并没有真正减去node.val,因此上一层函数的回调就会出错rest = rest - node.val;return rest == 0;}// 中:减掉当前节点rest -= node.val;// 左if (node.left != null) {// 向左探索boolean leftRes = hasTargetPath(node.left);// 在执行这个函数的时候,会执行rest -= node.left,因此下面的回溯要补回来if (leftRes) {// 说明左边探索出了一条可以的道路return true;} else {// 说明左侧没有符合要求的路径,此时要把rest恢复成没有向左探索之前的样子,来给右边探索铺路rest += node.left.val;}}// 右if (node.right != null) {// 向右探索boolean rightRes = hasTargetPath(node.right);// 在执行这个函数的时候,会执行rest -= node.right,因此下面的回溯要补回来if (rightRes) {// 说明左边探索出了一条可以的道路return true;} else {// 说明右侧没有符合要求的路径,此时要把rest恢复成没有向右探索之前的样子rest += node.right.val;}}// 如果左右两边都没有探索成功,那么就是失败return false;}
}
113.路径总和Ⅱ
要是有感觉不对劲的,print大法
class Solution {List<List<Integer>> res;LinkedList<Integer> currentPath;int rest;public List<List<Integer>> pathSum(TreeNode root, int targetSum) {res = new LinkedList<>();currentPath = new LinkedList<>();if (root == null) return res;rest = targetSum;traversal(root);return res;}void traversal (TreeNode node) {// 终止条件:node是根节点if (node.left == null && node.right == null) {rest -= node.val;currentPath.add(node.val);
// printAll();if (rest == 0) {System.out.println(222);LinkedList<Integer> temp = new LinkedList<>(currentPath);res.add(temp);}return;}// 中rest -= node.val;currentPath.add(node.val);
// printAll();// 左if (node.left != null) {traversal(node.left);// 回溯rest += node.left.val;currentPath.removeLast();
// printAll();}// 右if (node.right != null) {traversal(node.right);// 回溯rest += node.right.val;currentPath.removeLast();
// printAll();}}
//
// void printAll () {
// System.out.println("此时currentPath");
// for (int i = 0; i < currentPath.size(); i++) {
// System.out.println(currentPath.get(i));
// }
// for (int i = 0; i < res.size(); i++) {
// List<Integer> now = res.get(i);
// System.out.println("这是res中的" + i + "元素");
// for (int j = 0; j < now.size(); j++) {
// System.out.println(now.get(j));
// }
// }
// }
}
106.从中序与后序遍历序列构造二叉树
首先看一下手写是怎么构造的
就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来再切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
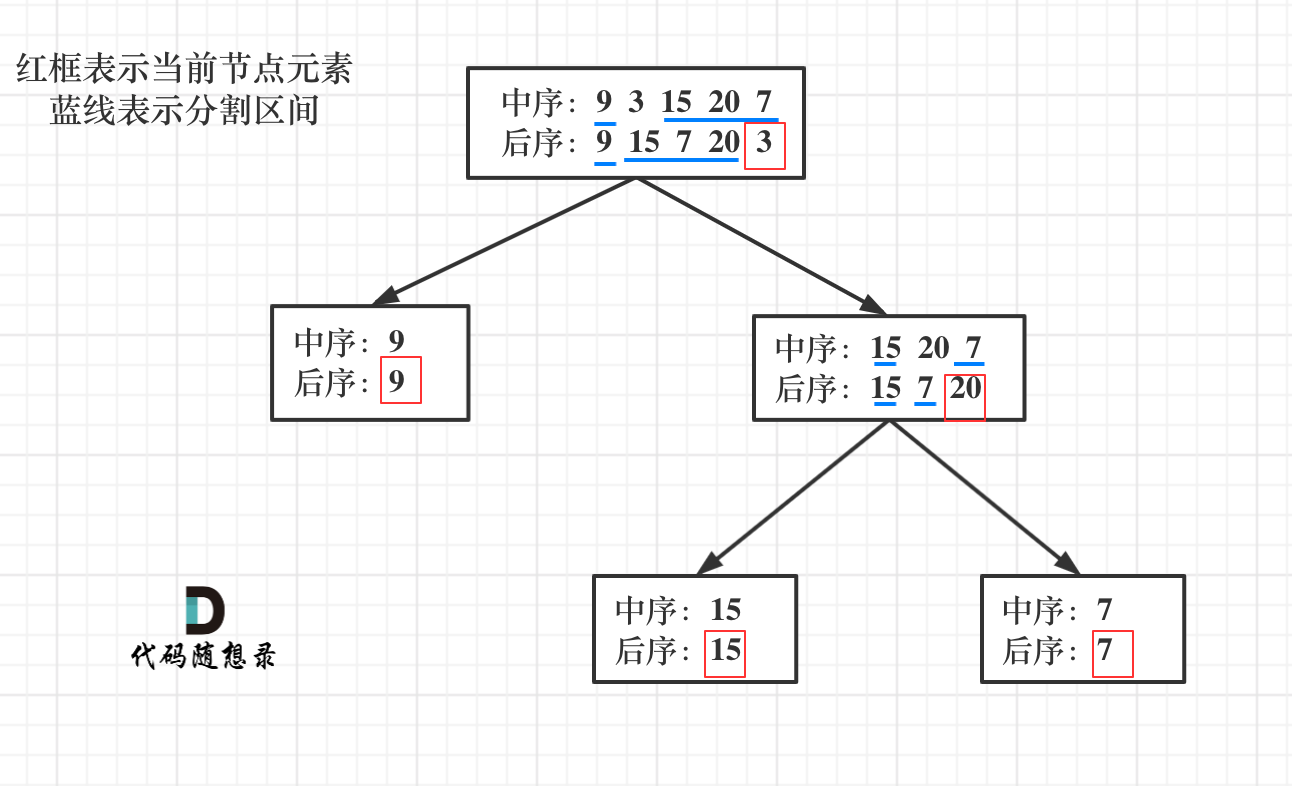
卡哥有云 :一层一层切割,就应该想到了递归。
递归函数traversal(inOrder, postOrder),入参是中序数组、后序数组,有返回值,返回值是以传进来的中序和后序数组构建的二叉树
现在枚举所有能产生返回值的情况:
- 如果inOrder的长度是0,返回null
- 如果inOrder的长度是1,返回这个唯一的元素
- 如果inOrder的长度 >= 2
- 找出后续最后一个元素,这是二叉树的根节点
- 在中序数组中找出这个元素,由此中序分为三部分
[inOrderLeft, root, inOrderRight] - 根据inOrderLeft, inOrderRight的长度把后续数组也切成三部分
[postOrderLeft, postOrderRight, root] root.left = traversal(inOrderLeft, postOrderLeft); root.left = traversal(inOrderRight, postOrderRight)- 返回root
这是每次递归都构造新数组,效率比较低。效率高的方法就是用下标来框定范围
public TreeNode buildTree(int[] inorder, int[] postorder) {TreeNode res = returnSubTree(inorder, postorder);return res;}TreeNode returnSubTree (int[] inorder, int[] postorder) {if (inorder.length == 0) return null;if (inorder.length == 1) return new TreeNode(inorder[0]);int rootVal = postorder[postorder.length - 1];TreeNode root = new TreeNode(rootVal);int rootIndexInInOrder = 0;for (int i = 0; i < inorder.length; i++) {if (inorder[i] == rootVal) {rootIndexInInOrder = i;break;}}int[] inOrderLeft = Arrays.copyOfRange(inorder, 0, rootIndexInInOrder);int[] inOrderRight = Arrays.copyOfRange(inorder, rootIndexInInOrder + 1, inorder.length);int[] postOrderLeft = Arrays.copyOfRange(postorder, 0, inOrderLeft.length);int[] postOrderRight = Arrays.copyOfRange(postorder, inOrderLeft.length, inOrderLeft.length + inOrderRight.length);root.left = returnSubTree(inOrderLeft, postOrderLeft);root.right = returnSubTree(inOrderRight, postOrderRight);return root;}
