算法日记day 23（有序数组转二叉搜索树|二叉搜索树转累加树|组合问题）

一、将有序数组转换为二叉搜索树

题目：

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵平衡二叉搜索树。

示例 1：

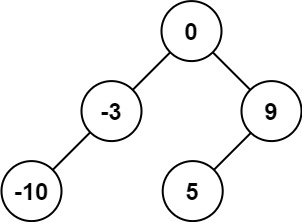
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

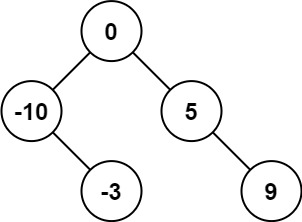
示例 2：

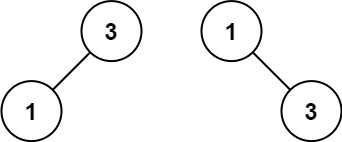
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

思路：

首先应根据下标找到数组中位于中间位置的元素作为构建平衡二叉搜索树的根节点，然后分别递归遍历该根节点的左数组和右数组作为其左子树和右子树

代码：

public TreeNode sortedArrayToBST(int[] nums) {// 调用 traversal 方法，传入 nums 数组、起始索引 0 和结束索引 nums.length - 1return traversal(nums, 0, nums.length - 1);
}public TreeNode traversal(int[] nums, int left, int right) {// 如果左边界大于右边界，说明没有元素需要处理，返回 nullif (left > right)return null;// 计算中间元素的索引int mid = left + (right - left) / 2;// 创建当前中间元素为根节点TreeNode root = new TreeNode(nums[mid]);// 递归构建左子树，范围是 left 到 mid - 1root.left = traversal(nums, left, mid - 1);// 递归构建右子树，范围是 mid + 1 到 rightroot.right = traversal(nums, mid + 1, right);// 返回构建好的根节点return root;
}

sortedArrayToBST 方法：
- 这是公共的方法，用于接收一个有序数组 nums，并调用 traversal 方法来构建平衡二叉搜索树。
- nums 是输入的有序数组，nums.length 表示数组的长度。
- nums.length - 1 是数组的最后一个元素的索引。
traversal 方法：
- traversal 方法是递归构建平衡二叉搜索树的核心方法。
- 参数：
  - nums：输入的有序数组。
  - left：当前子数组的起始索引。
  - right：当前子数组的结束索引。
- 递归终止条件：
  - 如果 left > right，说明当前子数组为空，直接返回 null。
- 构建根节点：
  - 计算中间元素的索引 mid，采用 (left + right) / 2 的方式，避免整数溢出问题。
  - 创建 TreeNode 对象 root，以 nums[mid] 作为当前子树的根节点值。
- 递归构建子树：
  - 递归构建左子树：调用 traversal(nums, left, mid - 1)，将左子数组范围 [left, mid - 1] 作为参数。
  - 递归构建右子树：调用 traversal(nums, mid + 1, right)，将右子数组范围 [mid + 1, right] 作为参数。
- 返回根节点：
  - 返回构建好的根节点 root。

二、二叉搜索树转换为累加树

题目：

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

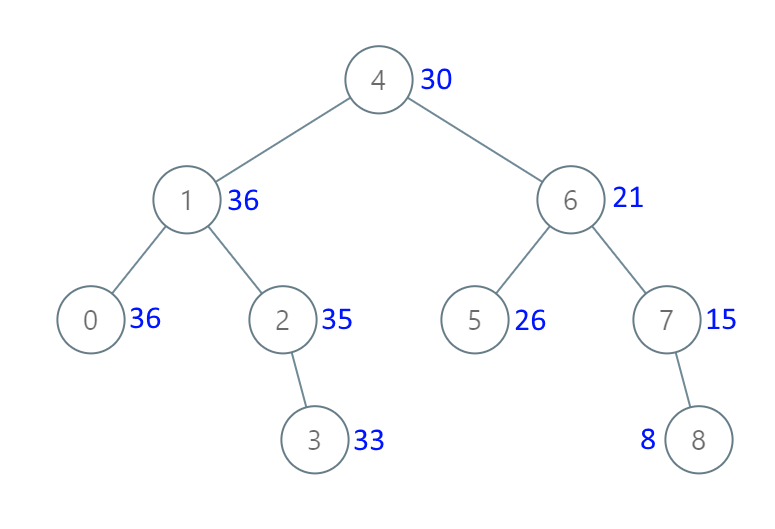
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

思路：

从题中不难得出，由于需要满足节点的新值大于等于当前节点的值之和，因此应该采用右、中、左的方式将节点的值逐渐累加最合适，定义一个计数器，采用双指针的方式不断记录前一个节点的值，另一个指针指向下一个节点，最终遍历完所有的节点

代码：

int sum = 0;public TreeNode convertBST(TreeNode root) {convert(root);return root;
}public void convert(TreeNode root) {if (root == null)return;// 遍历右子树convert(root.right);// 更新累加和sum += root.val;// 更新当前节点值为累加和root.val = sum;// 遍历左子树convert(root.left);
}

convertBST 方法：
- 公共方法，用于开始转换二叉搜索树为累加树（Greater Tree）的操作。
- 调用 convert(root) 方法来实际进行转换。
- 返回转换后的根节点 root。
convert 方法：
- 参数：root 是当前子树的根节点。
- 递归终止条件：如果 root 为 null，直接返回，表示当前子树为空。
递归转换过程：
- 右子树转换：首先递归调用 convert(root.right)，这一步确保先处理右子树，因为右子树中的所有节点都比当前节点大。
- 更新累加和：将 root.val 的值加到 sum 上，这样 sum 就成为所有大于等于 root.val 的节点值之和。
- 更新当前节点值：将 root.val 更新为 sum，这样就完成了当前节点值的转换。
- 左子树转换：最后递归调用 convert(root.left)，继续处理左子树。

三、递归与回溯解决组合问题

题目：

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

思路：

本题的关键在于如何进行回溯操作，当我们递归至某一元素后，满足条件打印输出返回上一层，否则继续向深层递归或者是返回空

模板

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

具体代码：

class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n, k, 1);return result;}public void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= n; i++) {path.add(i); // 将当前元素 i 加入组合中backtracking(n, k, i + 1); // 递归处理下一个位置，startIndex 变为 i+1path.removeLast(); // 回溯，将最后添加的元素移除，尝试下一个元素}}
}

成员变量：
- result：存储所有符合条件的组合结果的列表。
- path：保存当前递归过程中的一个组合。
combine 方法：
- 参数：n 表示 1 到 n 的范围，k 表示每个组合的长度。
- 返回值：返回一个列表，包含所有长度为 k 的组合。
backtracking 方法：
- 参数：n 表示范围上限，k 表示组合长度，startIndex 表示当前递归的起始位置。
- 递归终止条件：当 path 的长度等于 k 时，表示找到了一个长度为 k 的有效组合，将其加入 result 中，并直接返回。
递归过程：
- 循环遍历：从 startIndex 开始遍历到 n。
- 添加元素：将当前元素 i 加入 path 中，表示将 i 加入当前正在构建的组合中。
- 递归调用：递归调用 backtracking(n, k, i + 1)，将 i+1 作为下一次递归的起始位置，确保组合中的元素不重复使用。
- 回溯：在递归返回后，需要将最后添加的元素移除，尝试下一个可能的元素，以构建其他可能的组合。

这种属于是最原初的全部元素的遍历，但是实际上并不需要将全部情况都搜索一遍，因此还有优化空间（剪枝操作）

class Solution {// 存储所有符合条件的组合的结果集合List<List<Integer>> result = new ArrayList<>();// 当前递归路径中的一个组合LinkedList<Integer> path = new LinkedList<>();// 主函数，入口点，求解从 1 到 n 中长度为 k 的所有组合public List<List<Integer>> combine(int n, int k) {// 调用辅助函数进行递归求解combineHelper(n, k, 1);// 返回最终结果return result;}/*** 辅助函数，使用回溯算法求解组合问题* @param n 可选择的范围是从 1 到 n* @param k 当前需要选择的元素个数* @param startIndex 选择范围的起始位置*/private void combineHelper(int n, int k, int startIndex) {// 当路径长度等于 k 时，找到一个合法组合，将其加入结果集合中if (path.size() == k) {result.add(new ArrayList<>(path));return;}// 循环选择下一个元素加入当前组合中// 注意循环的上界进行了优化，避免不必要的遍历for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {path.add(i); // 将当前元素 i 加入组合中combineHelper(n, k, i + 1); // 递归处理下一个位置，startIndex 变为 i+1path.removeLast(); // 回溯，将最后添加的元素移除，尝试下一个元素}}
}

这里的循环终止条件做出的一定的改变，实际的优化是什么呢？

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)：循环从 startIndex 开始到 n - (k - path.size()) + 1，这里的优化保证了即使后面的元素都选择，也不会超过剩余需要选择的元素个数 k - path.size()。
i <= n - (k - path.size()) + 1; 循环继续的条件是 i 小于等于 n - (k - path.size()) + 1。这里的计算确保即使在当前递归层次中选择了最大可能的元素，也不会超过剩余需要选择的元素个数 k - path.size()。
n - (k - path.size()) + 1：这个表达式计算了当前递归层次可以选择的最大值。具体来说：
- n 是可选择的最大元素值。
- k - path.size() 表示还需要选择的元素个数。
- 因此，n - (k - path.size()) 是当前递归层次中可以选择的最大值。
- + 1 是为了确保循环可以达到 n - (k - path.size()) 这个值，因为在循环条件中是 <=，所以需要 + 1。

一个很简单的例子，如果n=4，k=4，那么在for循环遍历时，从2开始遍历就将没有任何意义的，这种的正是减少了不必要的循环遍历，提高了代码的执行效率

循环内部的代码逻辑是核心的组合生成部分，通过遍历从 startIndex 到 n - (k - path.size()) + 1 的所有可能的值，并递归调用 combineHelper 来生成下一层可能的组合。
每次循环体内的 path.add(i) 将当前的 i 值加入组合，然后递归调用会尝试在当前选择的基础上再选取下一个元素，直到满足长度为 k 的组合要求。

算法日记day 23（有序数组转二叉搜索树|二叉搜索树转累加树|组合问题）

一、将有序数组转换为二叉搜索树

二、二叉搜索树转换为累加树

三、递归与回溯解决组合问题

推荐新闻

热搜词