引言
幂律分布在游戏行业中非常重要。在免费游戏模式下,玩家的付费行为往往遵循幂律分布。少数“鲸鱼玩家”贡献了大部分的收入,而大多数玩家可能只进行少量或不进行付费。通过理解和应用幂律分布,游戏开发者可以更好地分析和预测玩家行为,优化游戏设计和运营策略,从而提升玩家体验和商业收益。本文介绍专门用于分析幂律分布的python库powerlaw,提供了丰富的工具来拟合、比较和可视化幂律分布及其他类型的分布(如指数分布、对数正态分布等)。
摘要
幂律分布是理论上非常有趣的概率分布,也经常用于描述实证数据。近年来,已经开发了有效的统计方法来拟合幂律分布,但适当使用这些技术需要显著的编程和统计洞察力。为了大大降低使用良好统计方法拟合幂律分布的障碍,我们开发了powerlaw Python包。这个软件包提供了用于基本拟合和分布统计分析的简单命令。值得注意的是,它还通过提供多种选项来支持用户的各种需求。源代码是公开的,并且易于扩展。
介绍
幂律分布是具有以下形式的概率分布:
p ( x ) ∝ x − α p(x) \propto x^{-\alpha} p(x)∝x−α
幂律概率分布在理论上是有趣的,因为它们是“重尾”的,这意味着分布的右尾仍然包含大量的概率。这种重尾性可能如此极端,以至于分布的标准差可能是未定义的(对于 α < 3 \alpha < 3 α<3 ),甚至均值也是未定义的(对于 $ \alpha < 2$ )。这些特性形成了一个无尺度系统,其中所有值都可能出现,没有特征大小或尺度。幂律分布在自然界中被广泛发现,包括在天体物理学、语言学和神经科学中。然而,准确地将幂律分布拟合到实证数据中,以及测量拟合的优度,并不是一件容易的事。此外,来自特定领域的实证数据可能伴随着需要在统计分析中考虑的领域特定因素。
近年来,已经开发了几种评估幂律拟合的统计方法。我们在此介绍并描述powerlaw,这是一个用于轻松实现这些方法的Python包。powerlaw包在现有软件的基础上有所进步,因为它易于使用,全面支持多种概率分布及其子类型,并且具有可扩展性和可维护性。包含多种分布类型和拟合选项是至关重要的,因为适当的分布拟合需要考虑数据的多个方面,否则拟合将不准确。代码库的易扩展性还允许未来扩展powerlaw的功能,特别是用户可以添加新的理论概率分布进行分析。
在本报告中,我们描述了powerlaw的结构和使用。使用powerlaw,我们将给出将幂律和其他分布拟合到数据的示例,并提供关于在此过程中应考虑的数据因素和拟合选项的指导。
图1展示了可视化、拟合和评估重尾分布的基本元素。每个组件在后续部分中有更详细的描述。图1和下面的powerlaw代码示例中包括了三个示例数据集,分别代表良好的幂律拟合、中等拟合和较差的拟合。第一个最佳拟合数据集可能是所有幂律分布中最著名和最坚实的:英语语言中的词频。使用的具体数据是赫尔曼·梅尔维尔的小说《白鲸》中的词频。第二个中等拟合数据集是秀丽隐杆线虫每个神经元的连接数。最后,较差拟合的数据是1984年至2002年间美国受电力中断影响的人数。
图1A显示了三个示例数据集的概率密度函数。图1B显示了只有分布的一部分尾部可能遵循幂律。图1C显示了幂律拟合的优度应与其他可能的分布进行比较,这些分布可能同样或更好地描述数据。
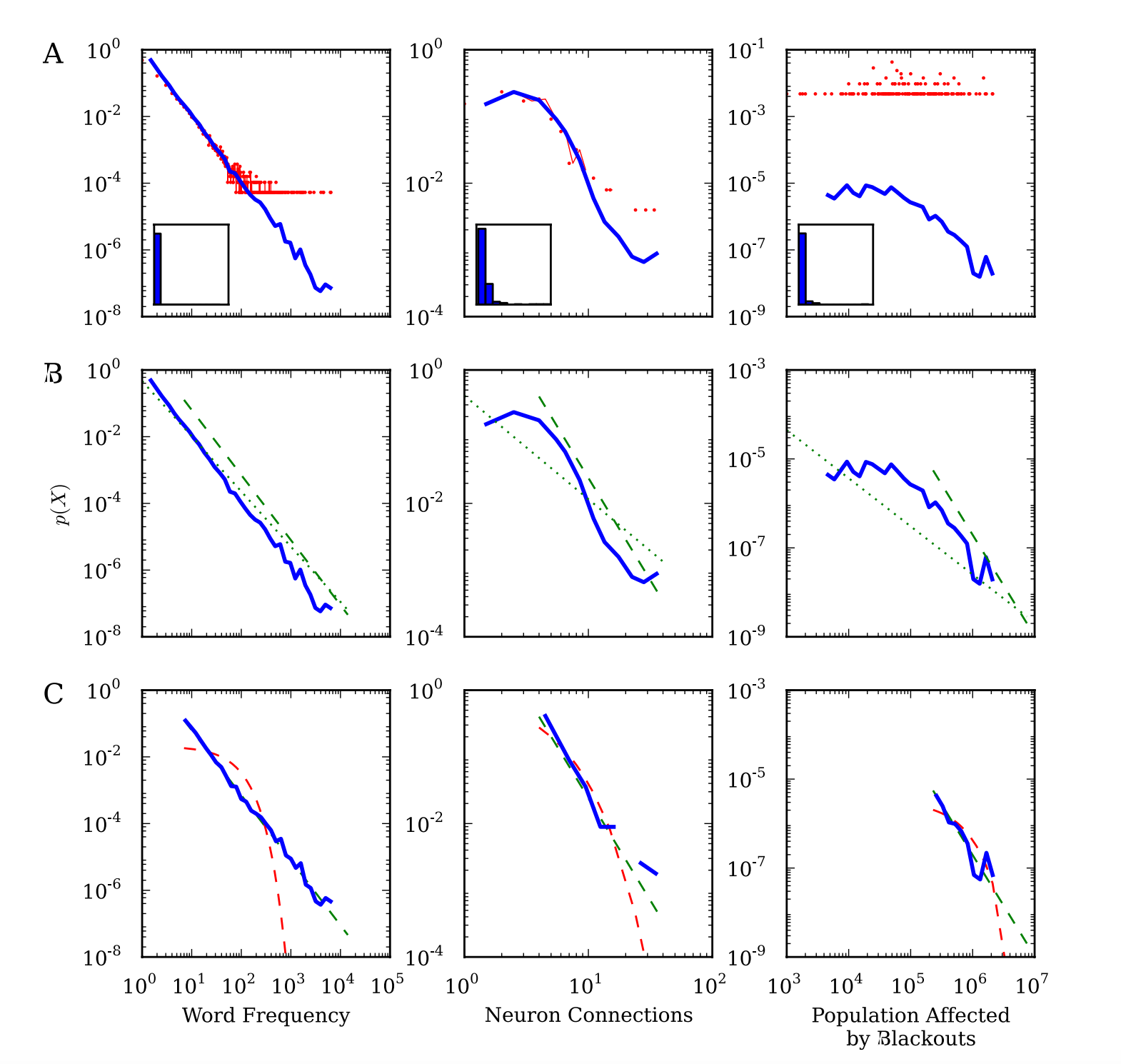
图1. 重尾分布分析的基本步骤:可视化、拟合和比较。幂律拟合的示例数据分别为良好拟合(左栏)、中等拟合(中栏)和较差拟合(右栏)。数据和方法在正文中描述。
a)使用概率密度函数可视化数据。在线性坐标轴上的典型直方图(插图)对于可视化重尾分布没有帮助。在对数-对数坐标轴上,使用对数间隔的箱是准确表示数据所必需的(蓝线)。线性间隔的箱(红线)会掩盖分布的尾部(见正文)。
b)拟合分布的尾部。最佳拟合幂律可能只覆盖分布尾部的一部分。虚线绿色线:从xmin=1开始的幂律拟合。虚线绿色线:从最佳xmin开始的幂律拟合(见基本方法:识别缩放范围)。
c)比较拟合优度。一旦确定了幂律的最佳拟合,就需要与其他可能的分布进行比较。虚线绿色线:从最佳xmin开始的幂律拟合。虚线红色线:从相同xmin开始的指数拟合。
powerlaw包将自动执行所有这些步骤。以下是powerlaw的基本用法示例,并附有解释。使用受停电影响的人口数据:
一个包含所有示例的IPython Notebook和原始Python文件包含在支持信息中。powerlaw的设计包括面向对象和函数式元素,用户可以使用这两种元素。面向对象的方法需要最少的代码行数,这里展示了这种方法。

powerlaw包围绕两种类型的对象组织:Fit和Distribution。Fit对象(上面的fit)是围绕数据集的包装器,它创建了一组拟合到该数据集的Distribution对象。Distribution对象是对特定分布的最大似然拟合。在上面的示例中,已自动创建了幂律Distribution(power_law),具有拟合的α参数alpha及其标准误差sigma。用户主要与Fit对象进行交互。
基本方法
可视化
powerlaw包支持概率密度函数(PDF)、累积分布函数(CDF;p(X < x))和补充累积分布函数(CCDF;p(X ≥ x),也称为生存函数)的轻松绘制。计算通过函数pdf、cdf和ccdf完成,而绘图命令是plot_pdf、plot_cdf和plot_ccdf。绘图使用matplotlib进行(见下文依赖项),并且powerlaw的命令接受matplotlib的关键字参数。图1A可视化了示例数据的PDF。
powerlaw.plot_pdf(data, color=’b’)
PDF需要对数据进行分箱,并且在对数坐标轴上呈现PDF时,分箱应具有对数间隔(指数增加的宽度)。尽管线性分箱在整个值范围内保持高分辨率,但分布中观察到大值的概率大大降低,无法可靠地估计其发生概率。通过使用对数分箱来补偿这一点,这增加了观察分布尾部一系列值的可能性,并适当地对分箱宽度的增加进行归一化。对数分箱是powerlaw的默认行为,但也可以通过linear_bins=True选项指定线性分箱。图1A显示了选择对数分箱而非线性分箱如何极大地改善数据分布的可视化。停电数据展示了一个特别严重的例子,其中数据的稀疏性导致单个线性分箱中数据点非常少,甚至包括空分箱。较大的对数分箱包含了这些数据的空白区域,以创建更有用的分布行为可视化。
powerlaw.plot_pdf(data, linear_bins=True, color=’r’)
由于CDF和CCDF不需要考虑分箱,因此CCDF常用于可视化重尾分布。然而,如果概率分布在尾部有峰值,这在PDF中比在CDF或CCDF中更明显。当分布有上限时,PDF和CDF/CCDF的行为也不同(见下文识别缩放范围)。
单个Fit对象还包括pdf、plot_pdf及其CDF和CCDF版本的函数。Fit内部的组成Distribution对象的理论PDF、CDF和CCDF也可以绘制。这些对于仅使用拟合分布的数据部分的可视化非常有用(如下所述)。要将多个图发送到同一图形,请使用关键字ax传递matplotlib轴对象。图2显示了神经元连接数据集的CCDF和PDF及其幂律拟合。注意,CCDF的缩放为α - 1,因此外观更浅。
fig2 = fit.plot_pdf(color=’b’, linewidth=2)
fit.power_law.plot_pdf(color=’b’, linestyle=’–’, ax=fig2)
fit.plot_ccdf(color=’r’, linewidth=2, ax=fig2)
fit.power_law.plot_ccdf(color=’r’, linestyle=’–’, ax=fig2)
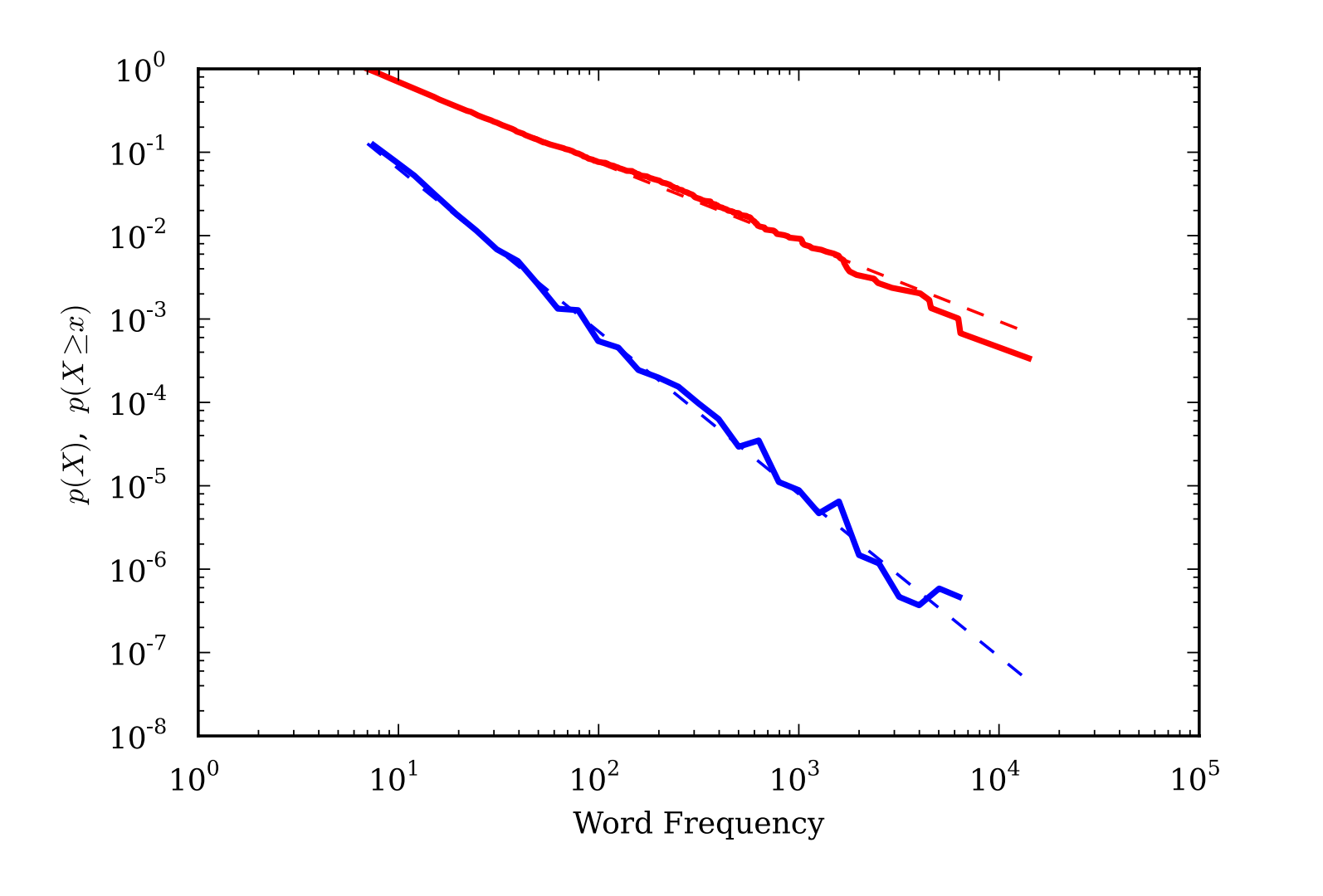
图2. 《白鲸记》中词频的概率密度函数(p(X),蓝色)和补充累积分布函数(p(X ≥ x),红色)。
PDF、CDF和CCDF信息也可以在绘图之外获取。Fit对象返回拟合数据的概率以及排序数据(cdf)或分箱边缘(pdf)。Distribution对象仅返回给定数据的概率。如果未给定数据,则使用所有拟合数据。
x, y = fit.cdf()
bin_edges, probability = fit.pdf()
y = fit.lognormal.cdf(data=[300, 350])
y = fit.lognormal.pdf()
识别缩放范围
拟合幂律的第一步是确定要拟合的数据部分。重尾分布的有趣特征是尾部及其属性,因此如果数据的初始小值不遵循幂律分布,用户可以选择忽略它们。问题是从哪个最小值xmin开始幂律的缩放关系。方法[5]通过从数据集中每个唯一值开始创建幂律拟合,然后选择导致数据与拟合之间Kolmogorov-Smirnov距离D最小的值来找到这个最优的xmin值。如果用户没有提供xmin值,powerlaw会在首次创建Fit对象时计算最优值。
由于幂律在x = 0时未定义,因此必须有一个最小值。因此,即使给定数据集带有特定领域的推理,认为数据必须在整个范围内遵循幂律,用户仍然必须指定一个xmin。这可以是理论最小值、噪声阈值或数据中观察到的最小值。图1B可视化了分配xmin = 1和通过最小化D找到最优xmin之间的拟合差异。以下powerlaw示例使用停电数据:

也可以将最优xmin的搜索限制在一个范围内,以元组或列表形式给出:

在某些领域中,可能还期望分布具有精确的上限xmax。上限可能是由于一个理论极限,数据无法超越该极限(例如在天体物理学中,速度分布的上限可能是光速)。上限也可能是由于有限尺寸缩放,观察到的数据来自更大系统的小子集。观察窗口的有限大小意味着单个数据点不能大于窗口xmax,尽管更大的系统会有更大、未观察到的数据(例如在神经科学中,从皮层的一部分记录与整个大脑记录)。可以通过实验性地改变观察窗口的大小(和xmax)并确定数据是否仍然遵循具有新xmax的幂律来测试有限尺寸效应。上限的存在依赖于数据的性质及其收集的上下文,因此只能由用户指定。拟合时会忽略任何超过xmax的数据。

默认情况下,Fit对象在计算或绘制CDF、CCDF和PDF时仅使用高于xmin且低于xmax(如果存在)的数据。Fit对象的绘图命令可以通过关键字original_data=True绘制最初提供的所有数据。组成的Distribution对象仅在xmin和xmax范围内定义,但可以通过关键字data传递特定数据来绘制该范围内的任何子集。
使用xmax时,幂律的CDF和CCDF在对数-对数图上不会呈现直线,而是在接近xmax时向下弯曲(图3)。相比之下,PDF在整个xmax范围内呈现直线。因此,当可视化具有xmax的数据时,PDF更为优选,以免掩盖缩放。
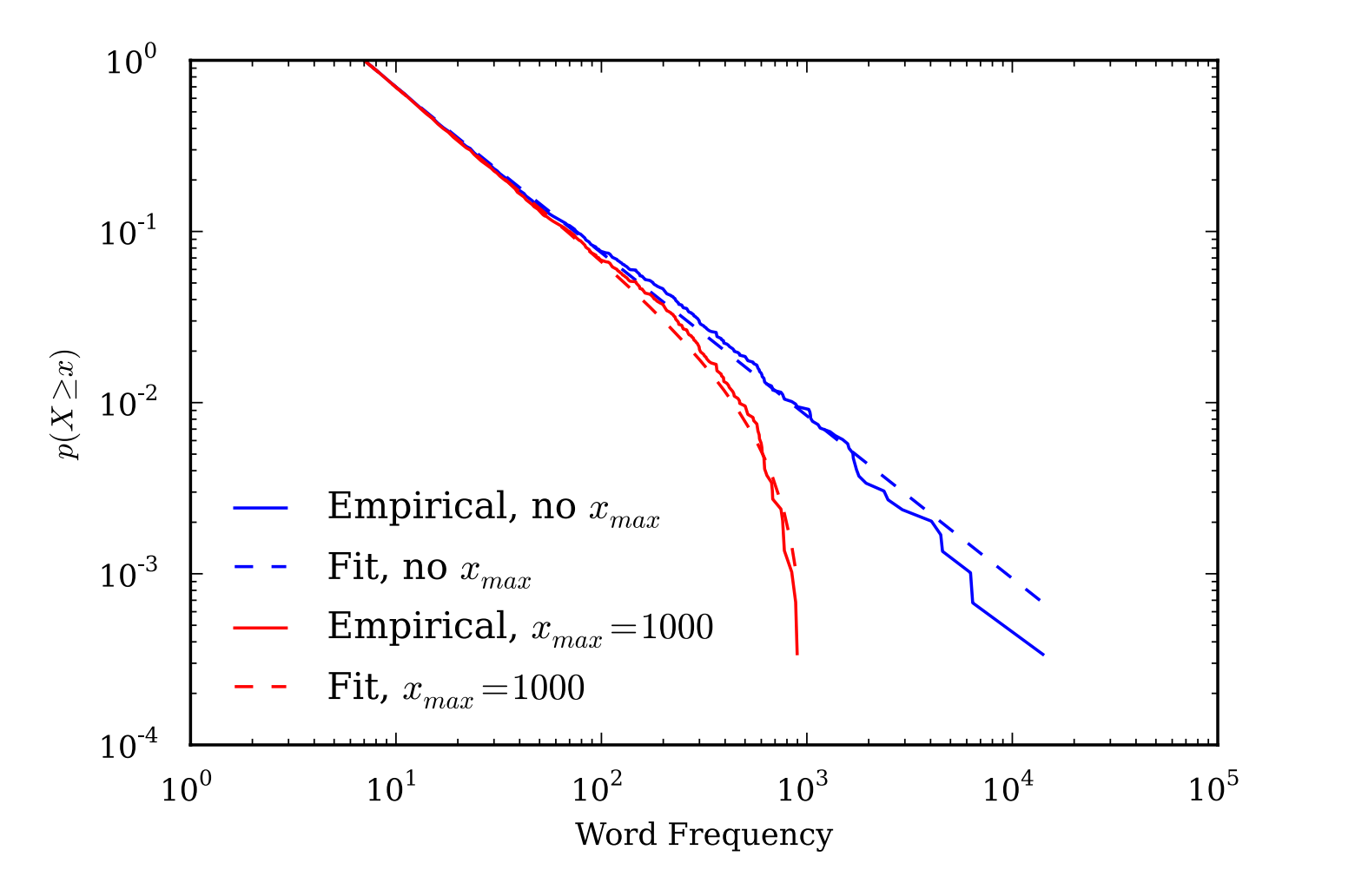
图3. 经验词频数据和拟合幂律分布的互补累积分布函数,有和没有上限xmax
连续数据 vs. 离散数据
数据集默认被视为连续的,因此适用于连续形式的幂律和其他分布。然而,许多数据是离散的。离散版的概率分布不能准确地用连续版来拟合。离散(整数)分布,通过适当的归一化,可以在初始化时指定:
离散形式的概率分布通常比连续形式更难计算,因此某些计算可能会更慢。然而,对于其中一些计算,有更快的估算方法。后续章节将描述这些加速离散概率分布计算的机会。
比较候选分布
从创建的 Fit 对象中,用户可以方便地访问评估重尾分布所需的所有统计分析。在 Fit 对象中,有不同可能分布的各个 Distribution 对象。每个 Distribution 都有该分布的最佳拟合参数(在调用时计算),可以通过参数的名称或更通用的“parameter1”访问。使用 blackout 数据:

在得出幂律是数据的良好描述之前,必须评估这些分布的拟合优度。每个分布的拟合优度可以单独考虑,也可以通过与其他分布的拟合进行比较来考虑(分别使用自举法和 Kolmogorov-Smirnov 测试生成单个拟合的 p 值 vs. 使用对数似然比来确定哪个拟合更好)。有几个实际和哲学上的理由,专注于后者,即比较测试。
实际上,自举法计算量更大,而对数似然比测试更快。从哲学上讲,回答一个分布“确实”遵循幂律的问题通常是不充分且不必要的。相反,问题在于幂律是否是可用的最佳描述。在这种情况下,知道自举测试通过是不够的;自举法确实可能发现幂律分布以足够的可能性生成给定数据集,但比较测试可能会发现对数正态拟合生成数据的可能性更大。另一方面,知道自举测试失败可能是不必要的;现实世界的系统有噪声,因此很少有经验现象能期望以理论分布的完美度遵循幂律。给定足够的数据,任何带有噪声或不完美的经验数据集总会在任何理论分布的自举测试中失败。如果严格遵守精确的理论分布,可能会陷入通过自举测试但数据量不足的困境。
因此,一般来说,更合理且更有用的是比较许多候选分布的拟合,并确定哪个拟合最好。图1C 直观展示了幂律和指数分布拟合的差异。这些分布拟合的优度可以使用 distribution_compare 进行比较。再次使用 blackout 数据:

R 是两个候选分布之间的对数似然比。如果数据在第一个分布中更可能,则该数值为正;如果数据在第二个分布中更可能,则该数值为负。该方向的显著性值为 p。normalized_ratio 选项通过其标准差 R / σ n R / \sigma \sqrt{n} R/σn对 R 进行归一化。归一化比率直接用于计算 p。
指数分布是评估分布重尾性时的绝对最小备选候选分布。原因是定义性的:典型的“重尾”定量定义是它不是指数有界的。因此,如果幂律不比指数分布拟合得更好(如上述示例),则几乎没有理由认为该分布是重尾的,更不用说是幂律了。
然而,指数分布再次只是描述概率分布时要考虑的最小备选候选分布。fit 对象包含 fit.supported_distributions 中支持的分布列表。任何这些分布名称都可以被 distribution_compare 使用。希望测试不支持的分布的用户可以按照源代码中描述的方式简单地将其写入 powerlaw。支持的分布中包括指数截断幂律,它在某个范围内具有幂律的缩放行为,但尾部被指数有界截断。还有许多其他不是幂律的重尾分布,如对数正态或拉伸指数(Weibull)分布。鉴于可能的候选分布数量无限多,可能会遇到类似于自举法的问题:总会有另一个分布更好地拟合数据,直到到达一个仅描述数据集中观察到的确切值和频率的分布(过拟合)。事实上,这种过拟合过程甚至可以从非常简单的分布开始;虽然幂律只有一个参数作为拟合的自由度,但截断幂律和替代的重尾分布有两个参数,因此具有拟合优势。通过在候选分布选择过程中引入生成机制,可以避免过拟合情景。
生成机制
观测数据总是来自特定领域,在该领域中生成机制创造了观测数据。如果有一个合理的领域特定机制可以生成特定的候选分布,那么应该考虑将该候选分布用于拟合。如果没有关于如何生成候选分布的假设,那么使用它来描述数据集的理由就少得多。
例如,线虫的每个神经元的连接数量似乎呈现出重尾分布(图1,中间列)。一个常见的生成幂律分布的机制是优先连接,这是一个“富者愈富”的增长模型。在线虫的这个领域中,连接数量多的神经元在有机体生长时可能会获得更多的连接,而连接数量少的神经元则很难获得更多的连接。优先连接机制会产生幂律分布,实际上幂律分布比指数分布更适合:

然而,线虫的大小是有限的,神经元的连接数量也是有限的,所以富者不能永远愈富。幂律的扩展可能会受到逐渐的上限效应的影响。指数截断幂律分布可能反映了这种限制。为了验证这一假设,我们比较了幂律分布和截断幂律分布:

实际上,两种分布都没有显著更好地拟合(p > .05)。从中我们只能得出对幂律分布的中等支持,而不排除指数截断的可能性。
在检查其他重尾分布时,考虑生成机制的重要性更大。也许最简单的生成机制是独立随机变量的累积,即中心极限定理。当随机变量相加时,结果是正态分布。然而,当正随机变量相乘时,结果是对数正态分布,这是一种非常重尾的分布。如果对数正态分布的生成机制在该领域是合理的,那么对数正态分布通常与幂律分布一样适合,甚至更好。图 4 展示了词频数据同样可以由对数正态分布和幂律分布很好地拟合(p > .05):

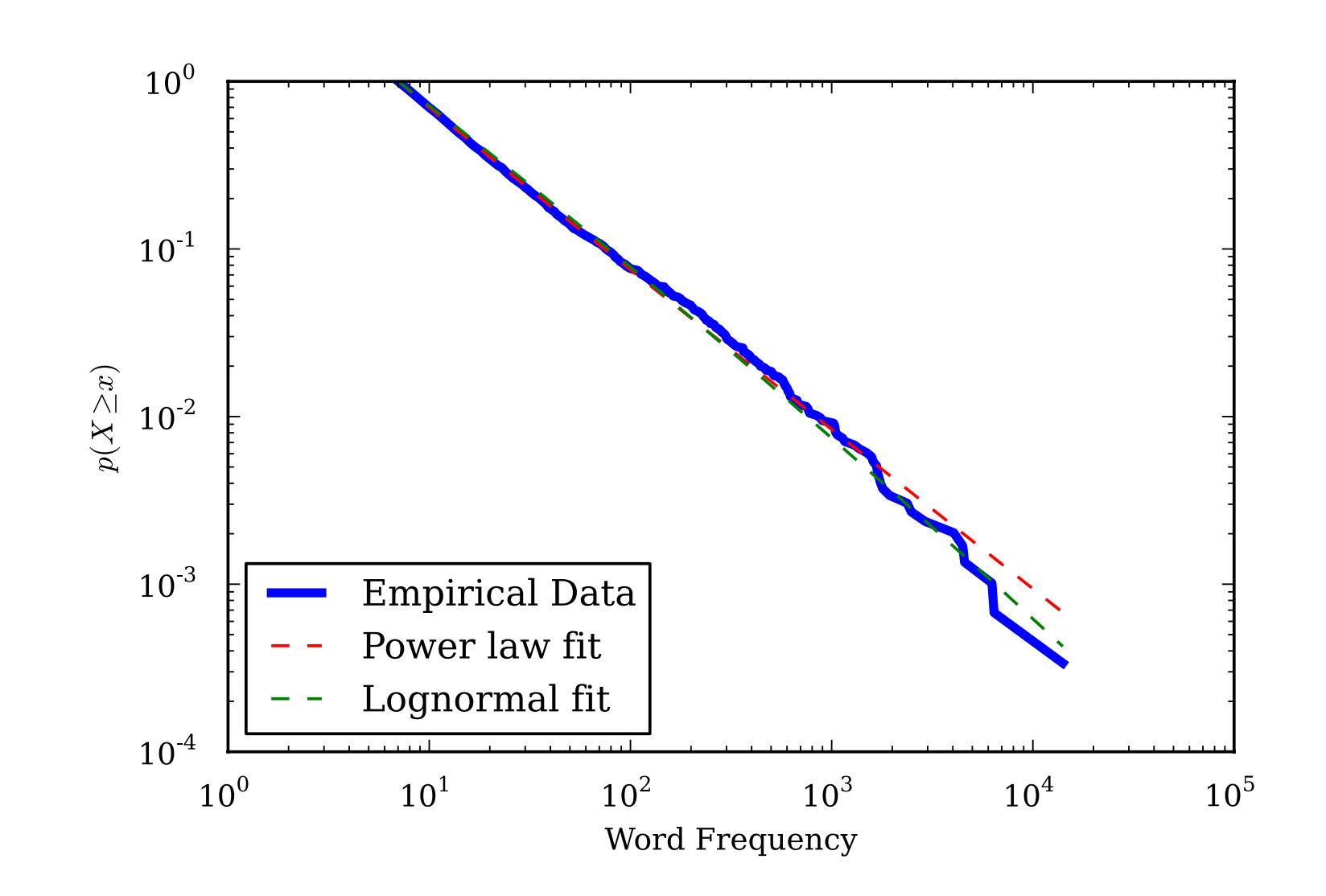
图 4. 词频数据的互补累积分布函数及拟合的幂律分布和对数正态分布。
在某些领域中,幂律分布比对数正态分布更适合。然而,区分幂律分布和对数正态分布的困难是常见且描述详尽的,类似的问题也适用于拉伸指数分布和其他重尾分布。面对这些困难时,重要的是记住假设和实验的基本原则:领域特定的生成机制为决定哪些重尾分布作为假设拟合提供了基础。一旦确定了候选分布,如果对数似然比检验无法区分它们,最强的解决方案是构建一个实验来识别哪些生成机制在起作用。、
创建模拟数据
从理论分布生成模拟数据对于各种任务(如建模)通常是有用的。单个分布对象可以使用函数 generate_random 生成随机数据点。这些分布对象可以从 Fit 对象调用或手动创建。

然后可以再次拟合这些模拟数据,以验证拟合软件(如 powerlaw)的准确性:

图 S1 显示了在各种参数值下,powerlaw 对 α 和 xmin 拟合的验证结果。
更多考虑事项
离散分布的计算和估计
虽然给定 xmin 的连续幂律分布的最大似然拟合可以通过解析方法计算,因此可以快速计算出最优的 xmin 和结果拟合参数,但离散情况下并非如此。离散幂律分布的最大似然拟合是通过数值优化找到的,对于每个可能的 xmin 值进行计算可能需要时间。为了解决这个问题,powerlaw 可以使用 [5] 中的 α 的解析估计,当不使用 xmax 时,该估计“在 xmin ≥ 6 时可提供约 1% 或更高的准确度”。默认情况下,estimate_discrete 选项为 True。
回到停电数据:

此外,一些分布的离散形式没有解析定义(例如,对数正态和伸展指数)。有两种可用的离散形式近似方法。第一种是通过蛮力离散化。使用分布的连续形式计算 xmin 和较大上限之间的所有离散值的概率。然后通过它们的总和对概率进行归一化。如果存在,可以将上限设置为特定值或 xmax。第二种近似方法是通过舍入进行离散化,其中连续分布被汇总到最接近的整数。在这种情况下,x 处的概率质量等于 x − 0.5 到 x + 0.5 之间的连续概率之和。由于其速度优势,这种舍入方法是默认方法。

从理论分布生成模拟数据在速度和准确性方面有类似的考虑。对于离散幂律分布的随机数据,没有快速、精确的计算方法。生成的数据可以通过快速近似或精确搜索算法计算,后者可能运行速度慢几倍 [5]。这两种选项可以通过 estimate_discrete 关键字选择,当使用 generate_random 创建数据时。

如果在调用 generate_random 时未明确指定是否使用估计,默认行为是使用生成数据的 Distribution 对象中使用的行为,该对象可能由用户创建或在 Fit 对象内创建。
theoretical_distribution = powerlaw.Power_Law(xmin=5.0, parameters=[2.5], discrete=True, estimate_discrete=False)
simulated_data = theoretical_distribution.generate_random(10000)
fit = powerlaw.Fit(empirical_data, discrete=True, estimate_discrete=True)
Calculating best minimal value for power law fit
simulated_data = fit.power_law.generate_random(10000)
随机数据的快速估计误差随 xmin 缩放。当 xmin = 1 时,误差超过 8%,但在 xmin = 5 时误差小于 1%,在 xmin = 10 时误差小于 0.2% [5]。因此,对于 xmin 较小的分布,精确计算可能是首选。
目前,其他非幂律分布的离散版本的随机数据生成方法都使用较慢的精确搜索算法。其他分布的快速、精确计算的估计可以稍后由用户实现,如下所述。
嵌套分布
比较嵌套版本的分布的似然性需要对所得的 p 值进行特定计算。是否分布是彼此的嵌套版本可以通过 nested 关键字指定。然而,如果不使用此关键字,powerlaw 会自动检测一个候选分布是否是另一个分布的嵌套版本,使用分布的名称作为指导。然后对 p 值的计算进行适当的修正。
这对于比较幂律分布和指数截断幂律分布最为相关,但对于指数分布和伸展指数分布(也称为韦伯分布)也是如此。

受限参数范围
每个分布对其参数范围都有默认限制(例如,幂律分布的 α > 1,指数分布的 λ > 0)。用户也可以提供自定义的参数范围。一种基本选项是关键字 sigma_threshold(默认值为 None),它将 xmin 的选择限制在产生 σ 低于阈值的那些范围内。

更广泛的参数范围可以通过关键字 parameter_range 设置,它接受一个参数名称的字典和一个包含其下限和上限的元组。这些参数范围并不是对 xmin 值的选择,而是限制了给定 xmin 的拟合考虑。

更复杂的参数范围可以通过传递一个函数给 parameter_range 来定义,以对参数进行任意计算。为了在 xmin 的优化中结合自定义参数范围,幂律参数范围应在 Fit 初始化时定义。

其他组成的分布对象可以在之后通过 parameter_range 函数单独赋予新的参数范围,如后面所示。
多种可能的拟合
随着不同参数要求的变化,xmin 的变化表明可能需要考虑多个拟合。假设没有 xmax,通过找到数据与该 xmin 值的拟合之间 Kolmogorov-Smirnov 距离 D 最小的那个 xmin 值来选择最优的 xmin。如果 D 在所有 xmin 值中只有一个局部最小值,这在理论上是简单的。然而,如果 D 在多个 xmin 上有相似 D 值的多个局部最小值,那么值得注意并考虑这些替代拟合。为此,Fit 对象保留了所有考虑过的 xmin 以及它们的 D、alpha 和 sigma 信息。回到因停电影响的人口规模数据,图 5 显示实际上有两个具有 D 局部最小值的 xmin 值,并且它们产生了不同的 α 值。第一个在 xmin = 50,D 值为 0.1,α 值为 1.78。第二个更优的拟合在 xmin = 230,D 值为 0.06,α 值为 2.27。

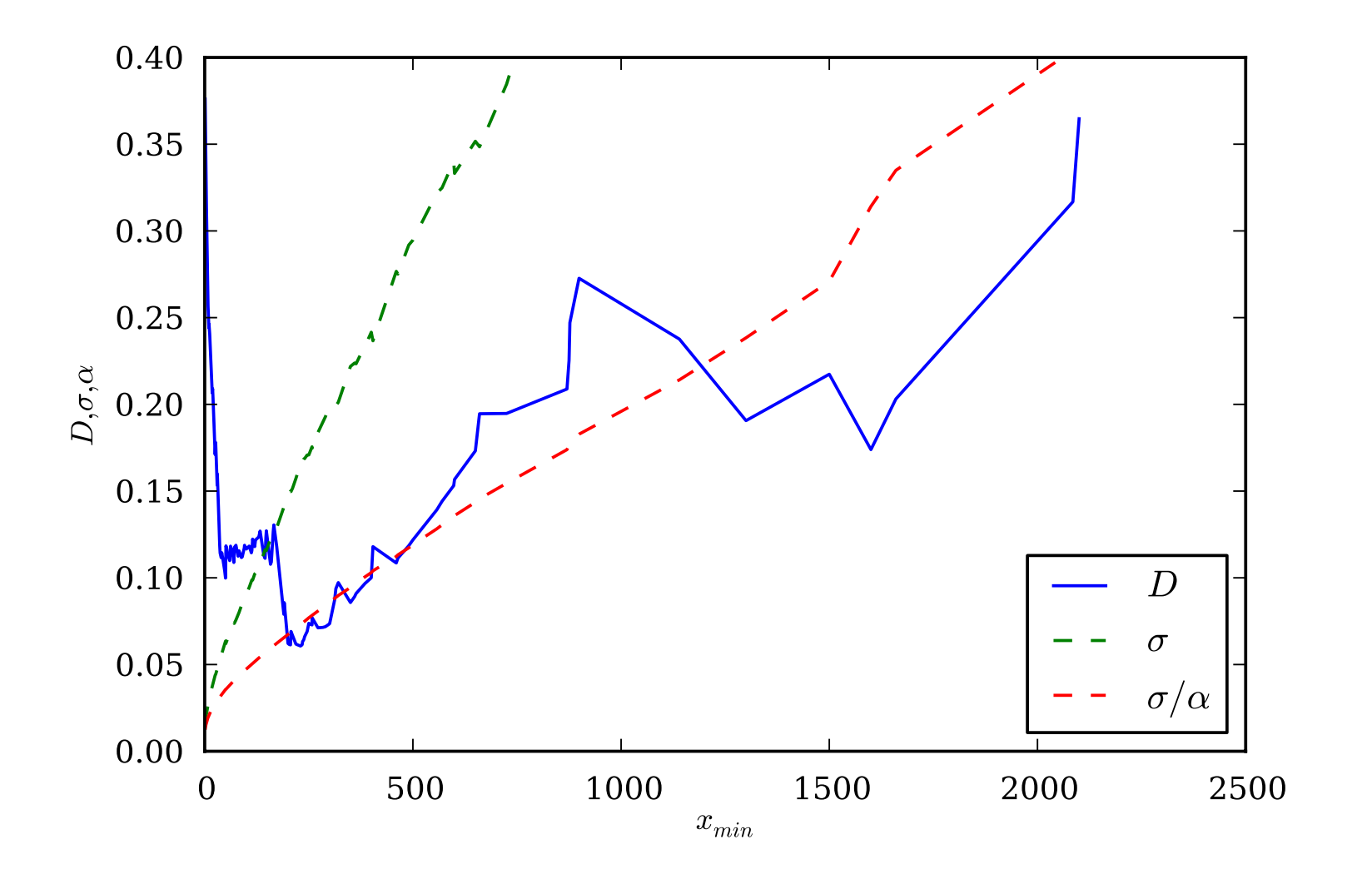
图 5. Kolmogorov-Smirnov 距离 D 在不同 xmin 上的多个局部最小值示例。当幂律分布从不同的 xmin 开始拟合数据时,幂律分布与数据之间的拟合优度通过 Kolmogorov-Smirnov 距离 D 来衡量,最佳的 xmin 最小化此距离。这里拟合的数据是受停电影响的人口规模。虽然 D 在 230 处存在一个明显的绝对最小值,因此 230 是最佳的 xmin,但额外的限制可能会排除这个拟合。参数要求如 σ < 0.1 或 σ/α < 0.05 会限制考虑的 xmin 值,导致识别出另一个不同的、更小的 xmin 为 50。
第二个最小值似乎显然是最优的。然而,σ 在整个 xmin 范围内几乎单调增加。如果用户对 σ 包含了参数拟合要求,例如 sigma_threshold=0.1,那么来自 xmin = 230 的第二个较低 D 值拟合将不被考虑。即使是更细微的参数要求,例如 σ/α < 0.05,也会排除第二个最小值。哪个 xmin 值的两个拟合更合适可能需要特定领域的考虑。
没有有效拟合
在将分布拟合到数据时,可能没有有效的拟合。这通常源于用户指定的要求,如通过 sigma_threshold 设置的 σ 最大阈值。可能没有一个 xmin 值的 σ 低于该阈值。如果发生这种情况,将忽略阈值要求并选择最佳的 xmin。Fit 对象的属性 noise_flag 将被设置为 True。

用户指定的参数限制也可能会在其他分布上造成计算困难。大多数其他分布是通过从初始猜测中搜索参数空间来数值确定的。初始猜测是使用有关分布形式的信息从数据中计算得出的。如果需要的极端参数范围远离标准参数范围的最佳拟合,初始猜测可能过于偏离,数值搜索将无法找到解决方案。在这种情况下,将返回初始猜测,并且 noise_flag 属性也将被设置为 True。通过提供一组初始参数进行搜索,即在用户提供的极端参数范围内,可以克服这种困难。


最大似然和独立性假设
用于拟合的最大似然方法以及用于比较不同分布拟合优度的对数似然比检验的一个基本假设是个别数据点是独立的。在某些数据集中,可能已知或预期观察值之间存在相关性。例如,在一个地理数据集中,某一山峰高度 X 的观察值可能与附近高度为 X/10 的山脚观察值相关。大的相关性可能会极大地改变最大似然拟合的质量。从理论上讲,这种相关性可以被纳入似然计算中,但这样做会大大增加拟合的计算要求。
根据相关性的性质,可以通过有选择地省略部分数据来“去相关”某些数据集。使用山脚的例子,已知相关的山脚可能出现在距离山峰 10 公里内,超过 10 公里相关性降为 0。要求山峰观察值之间的最小距离为 10 公里,并省略该距离内的任何额外观察值,将使数据集去相关。
最大似然估计的一个替代方法是最小距离估计,它通过最小化数据与拟合之间的 Kolmogorov-Smirnov 距离来拟合理论分布。这可以通过在初始化时使用关键字参数 fit_method=‘KS’ 在 Fit 对象中实现。然而,使用此选项并不能解决对数似然比检验中用于分布比较的相关数据点问题。
使用其他距离度量选择 xmin
最优的 xmin 定义为最小化经验数据与拟合幂律之间 Kolmogorov-Smirnov 距离 D 的值。然而,这个距离 D 对分布尾部的差异不敏感,而幂律的大多数有趣行为都发生在尾部。可能希望使用其他度量,如 Kuiper 或 Anderson-Darling,这些度量在测量分布之间的距离时对尾部给予额外权重。在实践中,Kuiper 距离 V 的表现并不显著优于 Kolmogorov-Smirnov 距离。Anderson-Darling 距离 A2 实际上过于保守,以至于会切除太多数据,导致数据点太少而无法进行良好拟合,尽管这对于在尾部有大量数据点的非常大的数据集可能不是问题。如有需要,powerlaw 支持使用这些其他距离选择 xmin,通过 xmin_distance 关键字调用(默认 ‘D’):

powerlaw 软件
可用性和安装
powerlaw 的源代码和 Windows 安装程序可从 Python Package Index(PyPI)获取,网址为 https://pypi.python.org/pypi/powerlaw。可以通过 pip 轻松安装:
pip install powerlaw
源代码也可以在 GitHub(https://github.com/jeffalstott/powerlaw)和 Google Code(https://code.google.com/p/powerlaw/)上获取。
依赖性
powerlaw Python 包完全用 Python 实现,需要 NumPy、SciPy、matplotlib 和 mpmath 包。NumPy、SciPy 和 matplotlib 是非常流行且稳定的开源 Python 包,适用于各种科学编程需求。SciPy 的开发由 Enthought, Inc. 支持,这三个包都包含在 Enthought Python 分发版中。mpmath 仅在拟合到伽马分布和指数截断幂律的离散形式时计算伽马函数时需要。如果用户不尝试拟合使用伽马函数的分布,则不需要 mpmath。SciPy 中的伽马函数计算对负数不准确。如果 SciPy 的伽马、gammainc 和 gammaincc 函数实现对负数变得准确,则可能会去除对 mpmath 的依赖。
powerlaw 的实用性和未来
已经有其他免费软件可用于拟合重尾分布。本文描述了这些软件包的设计和功能与 powerlaw 的差异。
如本文所述,拟合重尾分布涉及几个复杂的算法,并跟踪拟合数据集的许多选项和功能。powerlaw 使用 Fit 和 Distribution 对象的集成系统,因此用户只需与几行代码交互即可执行完整的分析流程。在其他软件中,这种集成不存在,用户需要编写更复杂的代码才能完全分析数据集。
在拟合数据时,用户可能需要或希望考虑多个分布族:幂律、指数、对数正态等。而且每个家族内有不同的风格:离散与连续,有或没有 xmax 等。powerlaw 在支持众多分布族及其所有风格方面目前是独一无二的。由于集成系统,用户无需做任何特殊或复杂的事情即可访问任何受支持的分布。目前没有其他软件包提供与 powerlaw 相同深度和广度的概率分布及其子类型的支持。
最后,许多现有软件并非为代码维护或扩展编写。powerlaw 的代码架构设计便于导航、维护和扩展。由于源代码维护在 GitHub 上的 git 仓库中,用户可以轻松提交问题、分叉代码和编写补丁。用户可能希望编写的最明显扩展是用于拟合数据和与幂律拟合进行比较的其他候选分布。所有分布都是 Distribution 类的简单子类,因此编写额外的自定义分布只需要几行代码。用户已经提交了建议并改进了某些分布,这些改进由于模块化组织的代码而能够无缝插入。此类贡献将在 powerlaw 的未来版本中继续添加。
