106、从中序与后序遍历序列构造二叉树

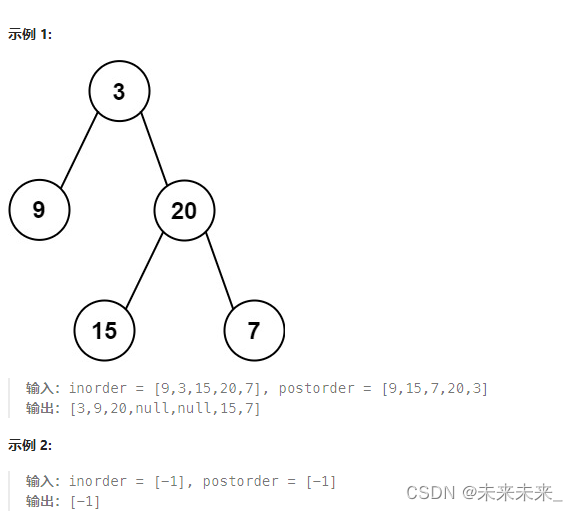
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

题解：要充分理解中序和后序的概念，后序的最后一个值就是根节点的值，由此找到根节点，再根据这个信息去分割中序数组，可以将中序数组分割为左中序和右中序，分割完成后左中序、右中序数组的大小就确定了。用这个大小也就可以去分割后序数组（注意是将后序最后一个元素去掉后分割，也就是将根节点剔除），同样后序数组也可以分割为左后序，右后序。这样将左中序、左后序组合，右中序，右后序组合进行递归，每次递归返回一个root节点，也就是最后会返回二叉树的根节点，完成整个二叉树的构建。

代码如下：

class Solution {
private:TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {if (postorder.size() == 0) return NULL;// 后序遍历数组最后一个元素，就是当前的中间节点int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);// 叶子节点if (postorder.size() == 1) return root;// 找到中序遍历的切割点int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组// 左闭右开区间：[0, delimiterIndex)vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);// [delimiterIndex + 1, end)vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );// postorder 舍弃末尾元素postorder.resize(postorder.size() - 1);// 切割后序数组// 依然左闭右开，注意这里使用了左中序数组大小作为切割点// [0, leftInorder.size)vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());// [leftInorder.size(), end)vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());root->left = traversal(leftInorder, leftPostorder);root->right = traversal(rightInorder, rightPostorder);return root;}
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (inorder.size() == 0 || postorder.size() == 0) return NULL;return traversal(inorder, postorder);}
};

注意：

1、对于这句代码的解释

vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);

• 向量声明和初始化：vector<int> leftInorder 声明了一个新的整型向量（vector<int>），名称为 leftInorder。

• 构造函数：(inorder.begin(), inorder.begin() + delimiterIndex) 是向量的构造函数，用于指定新向量的初始化方式。这里使用的是范围构造函数，它可以从另一个向量的一部分元素来创建新向量。

• 迭代器范围：

  • inorder.begin() 返回指向 inorder 向量第一个元素的迭代器。
  • inorder.begin() + delimiterIndex 返回指向 inorder 向量中从第一个元素起偏移 delimiterIndex 个位置的迭代器。注意，这个位置不包括在新向量中。

• 范围含义：inorder.begin() 到 inorder.begin() + delimiterIndex 之间的元素（包括起始位置的元素，不包括结束位置的元素）将被复制到新向量 leftInorder 中。

2、

前序和中序可以唯一确定一棵二叉树。

后序和中序可以唯一确定一棵二叉树。

那么前序和后序可不可以唯一确定一棵二叉树呢？

前序和后序不能唯一确定一棵二叉树！，因为没有中序遍历无法确定左右部分，也就是无法分割。