2024年数维杯国际大学生数学建模挑战赛参赛规则






数维杯大学生数学建模竞赛每年分为两场,每年上半年为数维杯全国赛(5月下旬) ,下半年为数维杯国际挑战赛(11月下旬),已连续成功举办九届,2023年数维杯国际大学生数学建模挑战赛共有近1.5万名学生参赛。参赛队伍来自国内外1177所高校,参赛高校覆盖清华大学、复旦大学、浙江大学、华中科技大学、天津大学、上海交通大学等高校。除中国大陆高校外,本次竞赛也吸引了来自世界一流加拿大多伦多大学、戴尔豪森大学、英国诺丁汉大学、利物浦大学、朴茨茅斯大学等境外高校参赛。目前竞赛具有较高的国际影响力,在国内高校中是作为保研、综合测评、创新奖学金等评定竞赛之一。
竞赛组织
内蒙古创新教育学会
内蒙古基础教育研究院
竞赛时间
报名截止时间:北京时间2024年11月15日06:00(周五)
竞赛开始时间:北京时间2024年11月15日09:00(周五)
竞赛结束时间:北京时间2024年11月19日09:00(周二)
论文提交截止:北京时间2024年11月19日09:00(周二)
承诺书提交截止时间:北京时间2024年11月19日09:00(周二)
竞赛结果公示时间:北京时间2025年1月上旬
参赛队员承诺
⑴.论文中所有图像,图形,图片,表格和附图如果不是队伍原创,就要在引用的位置标注。
⑵.所有的直接引语都放在了引号中进行标注,或者进行了特殊的引用注明。
⑶.授权数维杯国际大学生数学建模竞赛组委会,可将参赛论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
竞赛评阅原则
⑴.对赛题给出了满意的解读方法,并对模糊概念给予了必要的解释和说明;
⑵.明确列出了建模用到的前提条件及假设,并对其合理性给出解释或论证;
⑶.通过对赛题的分析给出建模的思路或论证建模的合理性;
⑷.设计出了能有效地解决赛题的数学模型;
⑸.对模型给出了稳定性的检验;
⑹.论了模型的优缺点,并给出了清晰的结论;
⑺.给出圆满准确的摘要。
竞赛时间
1
竞赛前
1.赛前准备
“数维杯”国际大学生数学建模挑战赛是面向所有在校大学生的竞赛,具有大学专科、本科、研究生学历的都可参加。每个队可以由一名、两名或 (最多允许)三名学生组成。根据历史的经验,最佳的组队是三个队员。在竞赛开始注册时,一个参赛队的学生可以跨校组队;在你们的参赛队中,并不要求要有一个数学专业的学生,团队成员可以是来自任何专业的学生。在组建了参加队之后,可以选择一个指导教师(鼓励学生不配备指导教师,独立参赛) 。
2.注册报名
⑴.全国各参赛队伍须在注册截止时间2024年11月15日06:00(周五)前完成报名工作;在线报名官网:https://www.nmmcm.org.cn/match_detail/34
扫描下方二维码
a.进入报名官网,点击位于屏幕右侧的立即报名,正确填写队伍信息进行注册报名;注意:报名截止后将不能再更改报名信息,确保使用的是当前有效的电子邮件地址以便我们在竞赛前、中、后的必要的时候可以联系到你。
b.如果你是学校集体报名的,请学校集体报名负责人,与竞赛工作人员联系。
⑵.注册费参赛高校需为每个参赛队伍缴纳100元参赛费。如果需要组委会提供详细的论文评价,需要再支付100元人民币的论文点评费(即每个参赛队支付200元人民币)。
⑶.个人报名通过报名官网缴费,学校集体报名,请联系竞赛工作人员,填写集体报名表统一缴费。个人通过报名网站报名完成后即可得到参赛编号,集体报名的队伍,由工作人员审核后获得参赛编号。
3.发票凭证
开票方式:开具增值税普通电子发票参赛队提供发票信息如下:学校全名称、纳税人识别号、地址、电话、开户行及账号注意:若不知道自己队伍的纳税人识别号就找自己的老师要果需要发票做报销用,请发邮件至fw@nmmcm.org.cn索取。为保证财务凭证顺利开具发票,请将转账汇款凭证放在附件中。注:数维杯数学建模竞赛开具的名称为:2024数维杯报名费。
2
竞赛中
1.赛题公布
竞赛题目将于2024年11月15日09:00(周五)准时发布,参赛队员可通过访问下面的网页:https://www.nmmcm.org.cn/match_detail/34 以及QQ官方群和获得赛题。
2.选题并作答
题目共分为4套(A题、B题、C题、D题) ,均以英文形式给出,题目类型分别为MCM(A、B题,比较注重理论和思路)和ICM(C、D题,比较注重实际应用),各参赛队可从4套题中任选一题,选择后不予更改。
每组参赛队伍必须提交一篇英文论文,参赛队要在规定时间内完成论文,赛事结束前将论文 电子版提交到组委会邮箱,相关注意事项详见《2024年数维杯国际大学生数学建模挑战赛论文格式规范及提交流程》。
3.竞竞赛要求及论文提交方式
①本次参赛作品统一在线提交到竞赛系统,截止时间之前可做多次提交,但只保留最后一次提交的文件。参赛作品包含电子版论文、承诺书、支撑材料 (有的情况下) ,竞赛论文只需提交英文形式电子档论文,不需邮寄纸质版论文、承诺书。提交的竞赛论文统一为PDF格式且以题号+报名组队编号命名的文件。(如 A2024000001.pdf)详见《2024年数维杯国际大学生数学建模挑战赛论文格式规范及提交流程》。
②备用邮箱(已在竞赛官网成功提交的队伍请不要重复发到备用邮箱)如果在提交时间内,竞赛官网无法正常提交(可能会出现高峰期时段) ,可将下面备用邮箱通道参赛论文提交到mcm@nmmcmorg.cn邮箱,各参赛队伍在比赛时间内可重复提交,以最后一次提交为准。
注: 邮件标题:题号+队号,例如A2024000001,各参赛队务必在竞赛结束前,将电子版论文、承诺书、支撑材料相关文件统一压缩后进行上传;在解答论文(正文开始)每一页的页眉上必须显示正确的参赛队队伍号和页码数。
例如,在每一页上使用下面的页标题:
A2024000001 Page1of20
压缩内容:电子版论文(命名与官网提交格式不变)、承诺书(命名与官网提交格式不变)、 支撑材料(命名与官网提交格式不变:选择性提交) ;过期无效,只允许上传一次;
压缩包支持文件格式:zip,rar
附件命名:题号+队伍号 例如:A2024000001.zip或rar;
邮件正文:可以不填写。
注意:比赛期间如遇到紧急情况可及时联系组委会工作人员进行解决。
竞赛论文提交截止时间:北京时间2024年11月19日09:00请务必在截止时间之前提交论文。原则上迟交的论文不参加评审,请各参赛队、指导教师高度重视。由于撰写、编辑论文需要较长的时间,其中还有很多的偶然因素,请各参赛队务必留足提交时间。不符合格式的论文将不予参加评审,涉嫌抄袭的论文将取消评奖资格。
3
竞赛后
1.评审的有关规定
竞赛组委会在全国范围内聘请有一定数学建模造诣的专家组成评审委员会,由评委会评委对提交论文进行评审。评委会及评委对组委会负责,不代表任何学校。评审按题目分组进行,每组设组长一名,一般由命题人担任。各组对赛题及参考答案进行充分讨论,结合样本论文反映出来的问题,综合假设的合理性,建模的创造性,结果的正确性和表述的清晰性等方面制定评审标准。评审流程一般包括初评、会评、复审和复议等过程。评委会将评审结果交组委会,由组委会按照竞赛章程进行结果公示、评奖等后续工作。
2.奖励设置
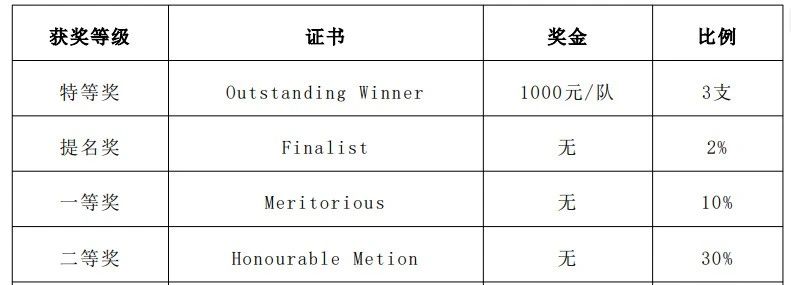
此次竞赛将设立等级奖和优秀指导教师奖、优秀组织奖,比例及奖品,具体如下图所示。
•优秀组织奖:可联系组委会申请协办并组织竞赛
•优秀指导教师奖:指导该参赛队伍荣获二等奖及以上的可颁发优秀指导老师证书(在报名时请填写好指导老师信息)
国际赛特等奖获奖队将获得1000元奖金,并有机会邀请参加2025年数维杯大学生数学建模冬令营 (暂定线下) 。竞赛将2025年1月上旬在官网上公示评审结果。
3.异议期的规定
⑴获奖名单公布之日起的一个星期内,公示期内组委会接受异议申请,异议申请需提供真实姓名和单位,组委会一般不受理要求提高奖项级别的申诉。
⑵公示期内接受违纪举报。违纪举报请务必实名并提供相关证据,组委会对违纪举报 进行调查,并有权取消确有违纪行为参赛队的获奖资格。
⑶针对初稿获奖名单,出现学校名称、姓名等错误信息的,请及时上报竞赛组委会。原则上只能改正错误的字,不能更换指导教师姓名、队员姓名,也不能添加队员等。
其他
竞赛官网:
https://www.nmmcm.org.cn/match_detail/34
2024年第九届数维杯大学生数学建模挑战赛顺利开赛,竞赛开始时间为北京时间2024年5月10日08:00至北京时间2024年5月13日09:00,共计3天,竞赛题目正式发布,快来一起围观,你认为今年的哪个题目更具有挑战性?欢迎评论区留言,同时预祝同学们在本届数维杯数学建模挑战赛中再创佳绩。以下为往届比赛赛题。
A题



B题




C题














import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 读取附件一的数据
df = pd.read_excel('热解数据统计.xlsx')
# 提取所需数据
data = df[['Mix_Ratio','Tar_%','INS_%','Water_%','Char_%']]
# 绘制散点图
plt.scatter(data['Mix_Ratio'], data['INS_%'])
plt.xlabel('mix ratio')
plt.ylabel('insoluble %')
plt.show()
# 计算交互效应
model = ols('INS_% ~ C(Mix_Ratio) + C(Tar_%) + C(Water_%) + C(Char_%) + C(Mix_Ratio)*C(Tar_%) + C(Mix_Ratio)*C(Water_%) + C(Mix_Ratio)*C(Char_%)', data).fit()
print(model.summary())
# 绘制交互效应图
fig = sm.graphics.plot_interaction.plot_interactions(model, plottype='effects', figsize=(12, 10))
plt.show()
# 分析交互效应
print(model.pvalues)
# 导入所需的库
import pandas as pd
import numpy as np
from scipy.optimize import minimize
# 读取附件一数据
df = pd.read_excel('热解数据统计.xlsx')
# 建立模型优化共解热混合比例
def optimization(x):# 定义共热解产物的理论计算值tar_theory = x[0]hex_theory = x[1]water_theory = x[2]char_theory = x[3]
# 计算共热解产物的实验值df['tar'] = df['CS'] * df['CS/HN'] * tar_theory + df['SD'] * df['SD/SM'] * tar_theory + df['GA'] * df['GA/NM'] * tar_theory + df['RH'] * df['RH/HN'] * tar_theorydf['hex'] = df['CS'] * df['CS/HN'] * hex_theory + df['SD'] * df['SD/SM'] * hex_theory + df['GA'] * df['GA/NM'] * hex_theory + df['RH'] * df['RH/HN'] * hex_theorydf['water'] = df['CS'] * df['CS/HN'] * water_theory + df['SD'] * df['SD/SM'] * water_theory + df['GA'] * df['GA/NM'] * water_theory + df['RH'] * df['RH/HN'] * water_theorydf['char'] = df['CS'] * df['CS/HN'] * char_theory + df['SD'] * df['SD/SM'] * char_theory + df['GA'] * df['GA/NM'] * char_theory + df['RH'] * df['RH/HN'] * char_theory
# 计算产物利用率和能源转化效率product_utilization = (df['tar'] + df['hex'] + df['water']) / df['total']energy_conversion = (df['hex'] + df['water']) / (df['tar'] + df['hex'] + df['water'] + df['char'])
# 计算误差平方和error = np.sum((product_utilization - df['product_utilization'])**2) + np.sum((energy_conversion - df['energy_conversion'])**2)
return error
# 设定初始值
x0 = [0.2, 0.3, 0.2, 0.3]
# 进行优化
res = minimize(optimization, x0, method='Nelder-Mead')
# 输出优化结果
print('优化后的共热解产物理论计算值为:', res.x)
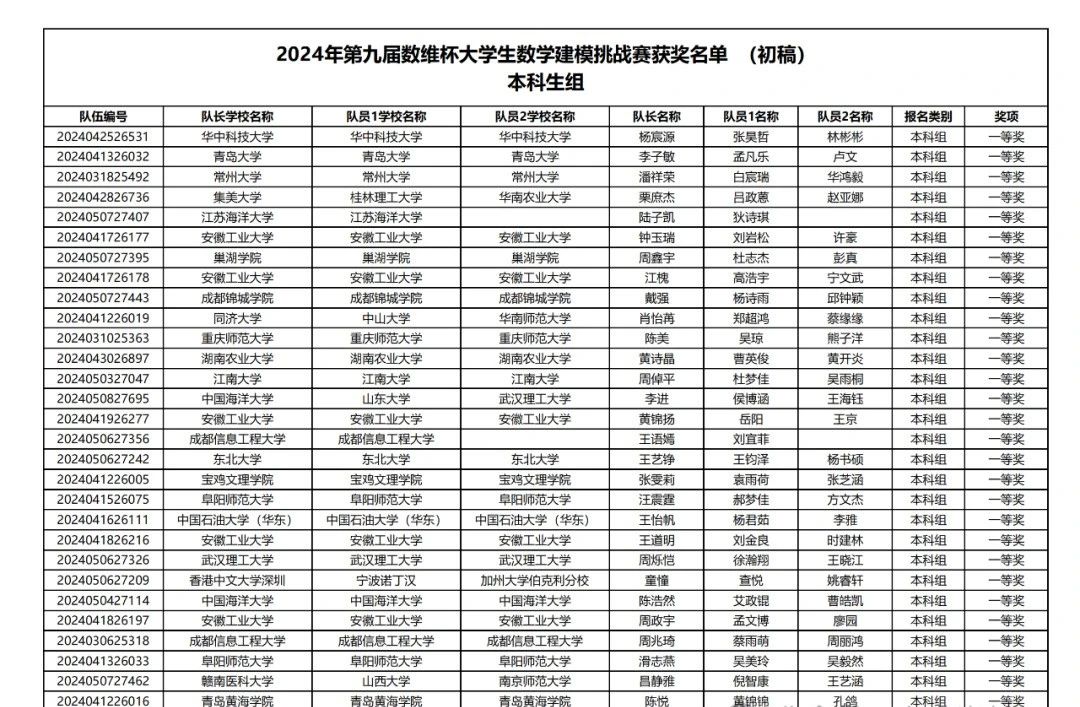
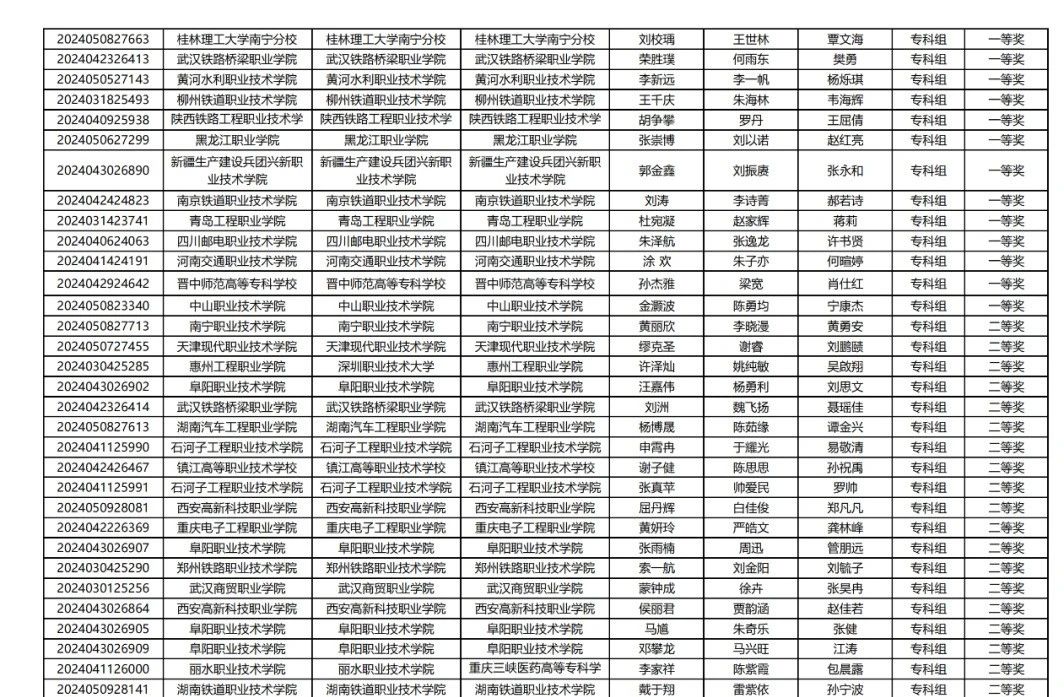
【初稿获奖名单】
2024年第九届数维杯大学生数学建模挑战赛
![]()
2024年第九届数维杯大学生数学建模挑战赛(小国赛)已结束,本次竞赛共有5143支队伍,近1.5万多名学生参赛,参赛队伍来自国内外909所高校, 39所985院校以及107所211院校。
最终共收到参赛论文4270份,竞赛专家组经过初评、复评、会评和最终审核四个阶段的评审,评选出一等奖214支,二等奖641支,三等奖1281支,优秀奖2011支,由于学术规范、格式错误等其它原因123支队伍未获奖。
电子版证书终稿后会陆续更新至数维杯官网,更新完可自行官网输入队伍号下载,纸质版证书由于面临学校放假,统一下学期开学后分批次邮寄,届时会发布邮寄通知。
获奖名单
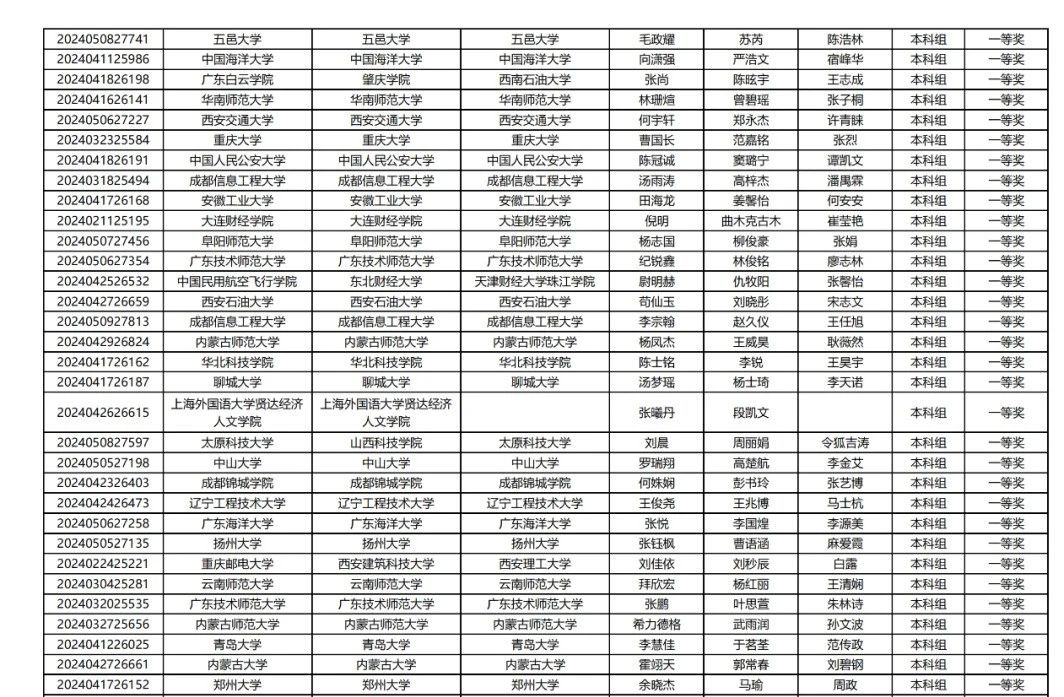
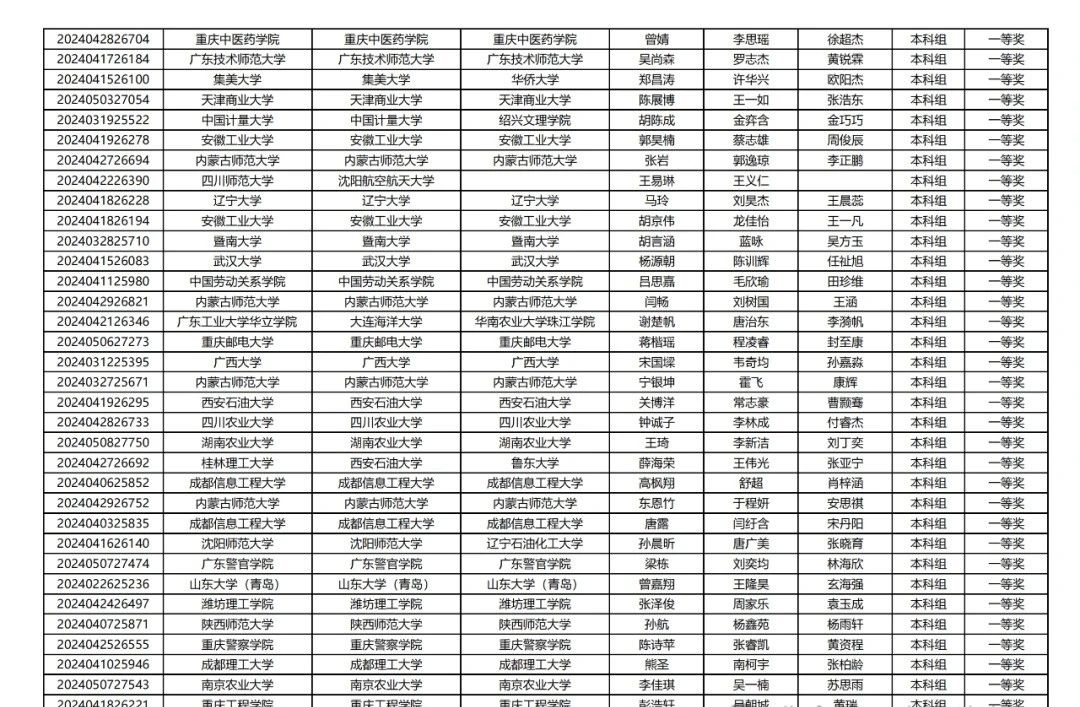
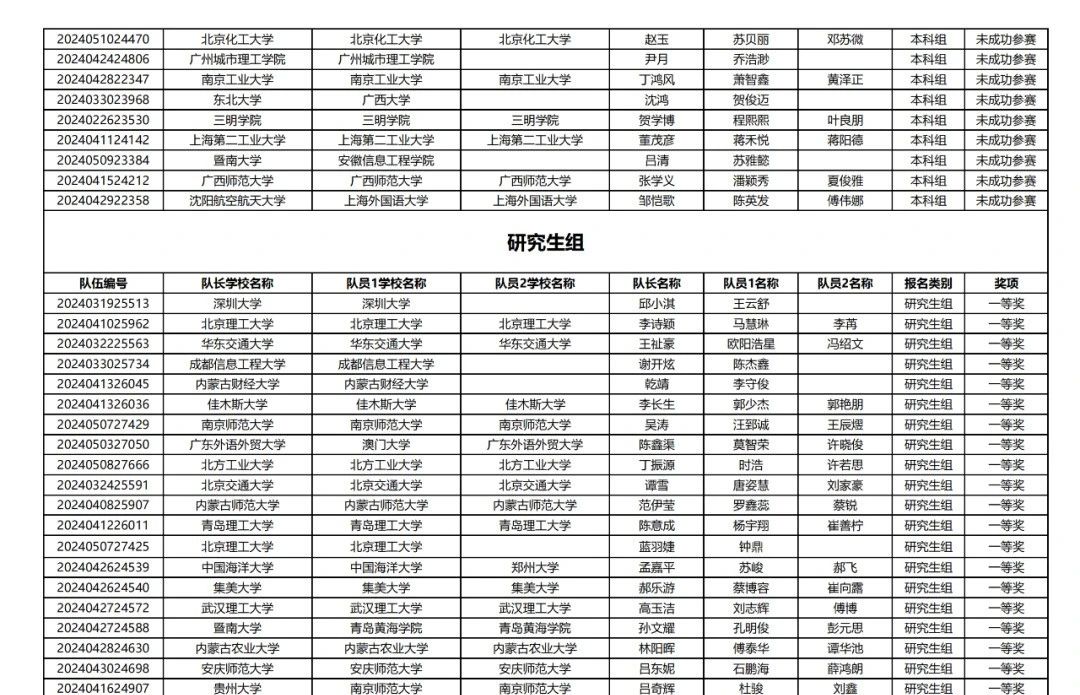
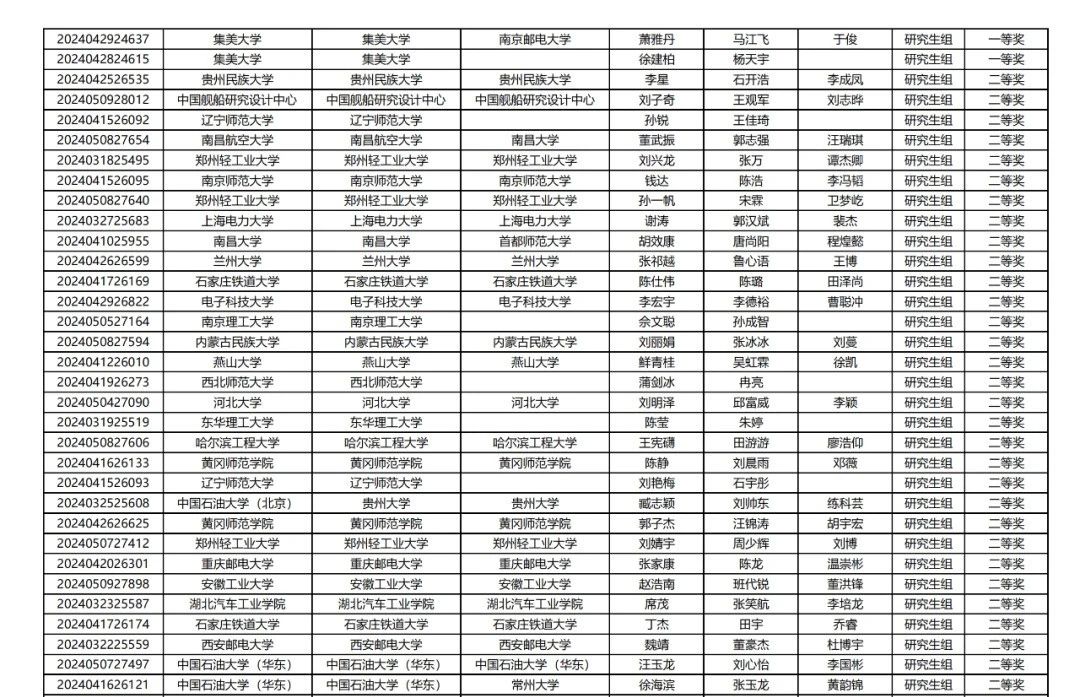
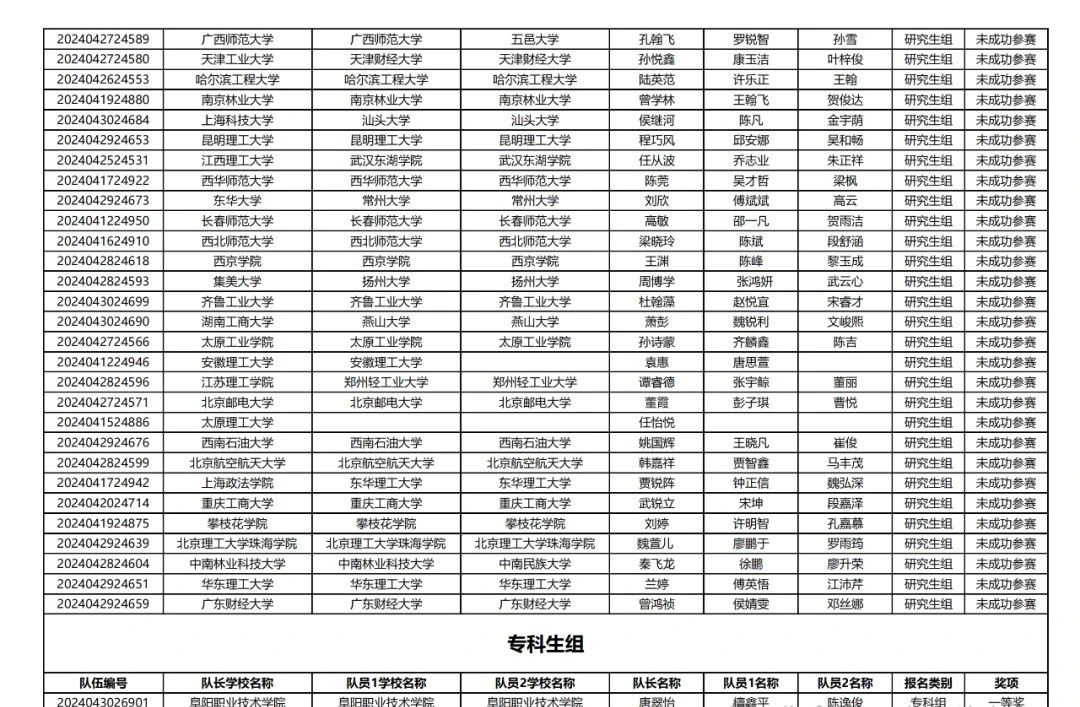
感兴趣小伙伴
