2024年10月08日 记录_导读
2024年10月08日 19:31
关键词
队列 线性表 假溢出 逻辑结构 物理结构 元素添加 数据结构 操作 元素 top 入栈 出栈 极限情况 size 函数 对比 结构 指针 链表 单链表
全文摘要
队列作为一种数据结构,以其先进先出的特性,在处理复杂问题如图和树的遍历中展现出重要性和灵活性。它作为受限线性表,与线性表的主要区别在于添加和删除操作的限制,尤其在解决实际问题时,队列的这些特性发挥着关键作用。文章深入讨论了队列的物理结构,包括使用数组和链表的存储方式,特别强调了循环队列的必要性以避免假溢出问题。同时,通过实例阐述了栈的数据结构,包括其基本属性和操作,以及与顺序表的结构和操作的区别和相似性,强调了对这些基础数据结构理解和掌握的重要性。此外,讨论了单链表的基本操作和应用,以及如何利用栈的数据结构进行中缀表达式到后缀表达式的转换,进一步说明了递归在解决复杂问题中的应用和递归与迭代的区别。这些讨论不仅加深了对数据结构的理解,也揭示了它们在算法实现和问题解决中的核心作用。
章节速览
00:00 理解队列结构及其在解决问题中的应用
讨论了队列作为数据结构的重要性和灵活性,强调了它在处理复杂问题时的作用,如遍历图和树结构。介绍了队列的定义,其作为受限线性表的特性,以及与线性表的区别,特别是关于添加和删除操作的限制。还提到队列的两种访问模式:先进先出和后进先出,以及如何利用队列的这些特性解决实际问题。
06:00 数据结构:队列的逻辑与物理结构
本文详细介绍了数据结构中的队列,从逻辑结构出发,阐述了队列的基本概念。随后,讨论了队列的物理结构,包括使用数组和链表存储的两种主流方式,特别强调了循环队列的必要性,以解决普通队列存在的假溢出问题。文章最后指出,队列的操作虽然简单,但重点在于如何利用队列解决实际问题,同时解释了“顶部”和“底部”的概念,并对不同表述的适用性进行了说明。
12:31 理解栈的运作原理和操作过程
在讲解栈的概念时,我们首先明确了栈的基本属性,包括’空’和’满’的状态,以及入栈和出栈的基本操作。通过实例化一个空栈,并详细解释了入栈操作的过程,包括top指针的移动和元素的存储。进一步地,讨论了栈的满状态及其对入栈操作的限制,同时指出链表与栈在操作上的区别,以及在实现上如何通过数组来限制栈的大小。此外,还强调了对栈中操作的理解和实践,包括如何通过出栈操作来读取元素,以及如何将元素取出后更新top指针。最后,通过对比栈与顺序表的结构和操作,指出了它们的相似性和区别,强调了理解和掌握这些结构的重要性。
21:25 理解单链表及其操作
讨论了单链表的基本概念,包括节点的添加、删除等操作,强调了在操作中避免指针丢失的方法。同时,指出了单链表在不同场景中的应用,并鼓励学习者通过实际操作来加深理解。
30:30 利用栈检查对称性
讨论了使用栈数据结构检查对称性的方法,以括号匹配为例。通过读取字符串中的字符,对于左括号入栈,遇到右括号时检查栈顶是否匹配,不匹配则中断。循环处理直至字符串结束,最后判断栈是否为空来决定是否对称。这种方法简洁有效,强调了基础数据结构的应用和熟练掌握基础操作的重要性。
38:11 表达式求值与进制转换原理
本对话围绕计算机中数字进制转换和表达式求值两种算法展开讨论。在进制转换方面,讲解了如何将数字从一个进制转换到另一个进制,通过不断除以目标进制并记录余数来实现,强调了倒读余数的过程。在表达式求值部分,解释了计算机如何处理数学表达式,从中缀表达式转换为后缀表达式(逆波兰表达式),以便更容易计算结果,重点说明了运算符优先级和括号如何影响计算顺序。
44:23 中缀表达式与后缀表达式之间的转换方法
讨论了中缀表达式到后缀表达式,以及后缀表达式回转为中缀表达式的方法。首先,对于简单的表达式,提倡手动分析转换,以直观理解转换过程。接着,当面对复杂表达式时,提出通过编写程序实现自动转换的想法。详细讲解了利用栈结构进行转换的原理,包括两个栈的使用:一个用于存储操作数,另一个用于存储运算符。强调了符号优先级的重要性,特别是括号的作用和其优先级的变化,指出括号在栈外时具有极高的优先级,但一旦进入栈中,其优先级降低。通过形象的比喻(寺庙门槛),进一步说明了运算符(尤其是括号)优先级的动态变化机制,为理解中缀与后缀表达式的转换提供了清晰的指导。
47:54 栈的应用:中缀表达式到后缀表达式的转换
讨论了如何利用栈的数据结构来实现中缀表达式到后缀表达式的转换,进而求解数学表达式的值。首先,通过构造两个栈,一个用于存储运算对象,另一个用于存储运算符号,利用栈的特性(先进后出)进行表达式的解析。在解析过程中,遇到运算对象时入运算对象栈,遇到运算符时根据运算符的优先级决定其是否入运算符栈,同时处理运算符栈顶元素与当前运算符栈的关系,实现运算符栈中元素的出栈和运算。通过举例分析,展示了整个转换过程及运算步骤,强调了栈在表达式求解中的关键作用。
53:57 理解递归及栈的使用
讨论了递归的概念,强调了递归在编程中的重要性及其实现机制。递归是函数调用自身的过程,通过栈数据结构来记录和回溯调用过程中的位置,确保程序能从一个调用返回到另一个调用点。同时,解释了递归与迭代的区别,并通过阶乘计算的例子说明了递归解决问题的逻辑。递归通过不断减小问题规模,直到达到一个已知的简单情况(基本情况),从而逐步求解复杂问题。此外,还提到了递归在处理如树结构数据时的运用,特别是在提取和处理叶子节点时的作用。
思维导图
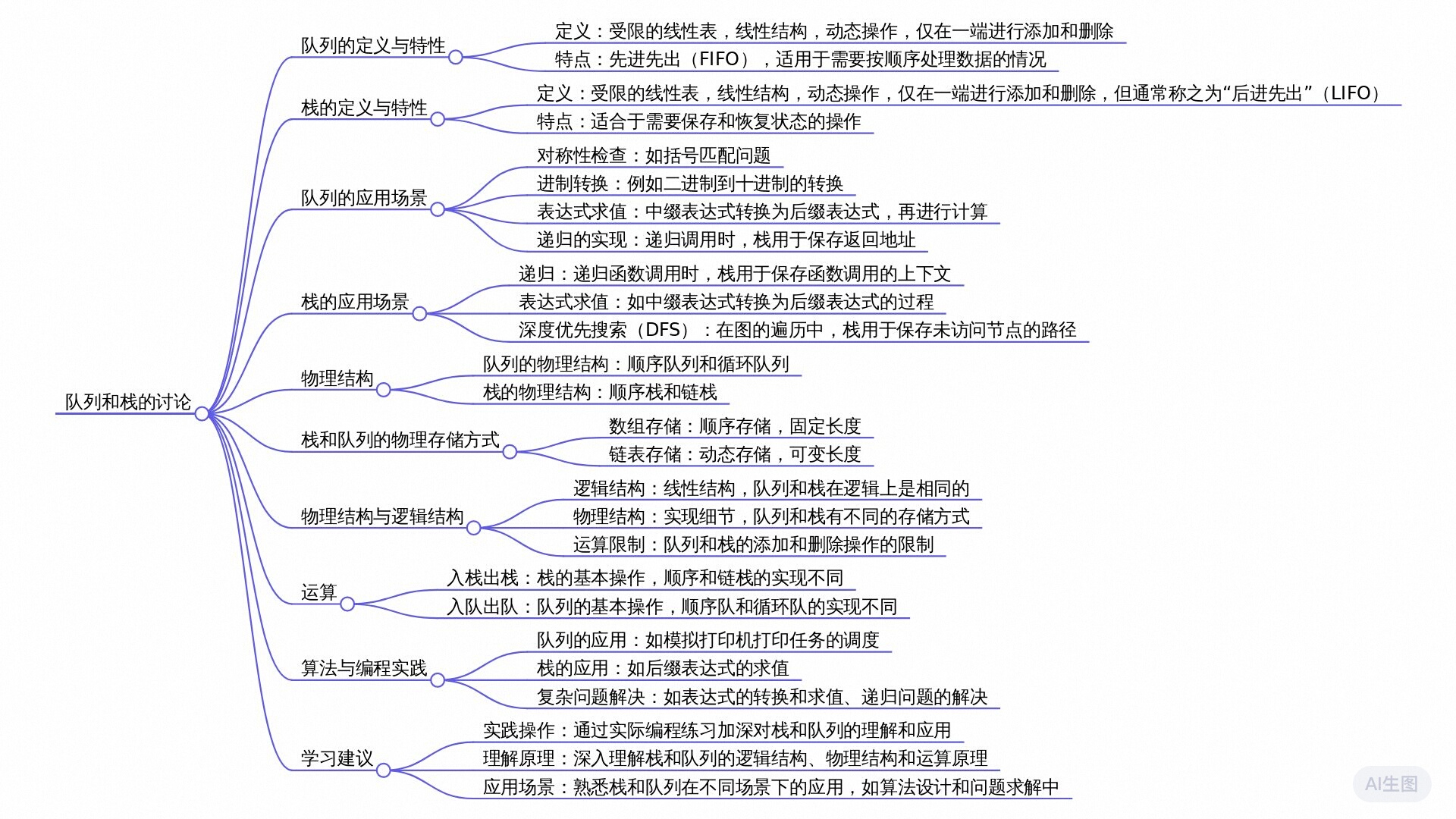
要点回顾
队列作为一种受限线性表,其主要特点是什么?
队列作为受限的线性表,其特点是动态结构下进行的添加和删除操作只能在一端进行,这是它受限的运算性质所决定的。例如,在线性表中允许在任何位置进行插入或删除,而队列则严格限制在一端插入元素,在另一端移除元素,这就形成了数据的先进先出(FIFO)或后进先出(LIFO)特性。
在队列的应用场景中,为何需要借助计算机计算能力?
在处理诸如成百上千个节点的图或者自然界中一棵树的情况时,手动记录和操作可能会导致遗漏或重复问题。通过利用计算机的计算能力,我们可以设计出遵循特定规律的算法,以确保一次性、不重复地读取和写入所有节点,这是队列作为灵活工具的重要作用。
队列和栈的主要区别是什么?
队列和栈都是运算受限的线性表,但它们在运算操作上有本质的区别。队列采用先进先出(FIFO)原则,元素的进出顺序是固定不变的;而栈采用后进先出(LIFO)原则,元素的进出顺序相反。在实际应用中,当需要模拟现实生活中的队列(如售票场景)时,应使用循环队列(环队列)来代替普通的顺序队列,以防止因先进先出规则引起的假溢出问题。
队列如何通过循环队列解决普通队列可能产生的“假溢出”问题?
当队列达到其容量上限而无法继续添加元素时,会出现“假溢出”现象。为避免这种情况,循环队列(环队列)引入了循环计算机制。例如,通过使用模运算去除以队列的最大容量,使得即使在队列末端仍然有空位的情况下,新元素也能成功加入,从而有效解决了普通队列因先进先出特性导致的假溢出问题。
在数据结构中,“占比”是如何定义的?如何确定数组中的“底部”和“顶部”位置?
在我们这本书中,“占比”是一个固定的概念,它以数组最零下标位置作为基准,固定成为占比。而在其他教材或表述中,可能会用“base”表示底部,“top”表示顶部,但本质上都是为了简化问题和便于理解。在操作过程中,虽然底部是固定的,但顶部可以灵活移动。我们可以通过两个哨兵(base和top)来限定底部和顶部。即使顶部在进行操作时可以移动,但只要有一个固定不变的底部(例如数组的最零下标位置),就能确定顶部的位置。
在顺序栈中,如何判断空和满状态?
在顺序栈中,有特殊的两个位置代表空和满状态,即top等于-1表示为空状态,而当top等于max size减1时,则表示已达到满状态,此时不能再进行元素添加操作。在链表实现中,由于没有明确的满状态,所以只有空状态。
顺序栈的入栈和出栈操作流程是怎样的?
顺序栈的入栈操作包括两步:首先,将元素放入数组中;其次,将top值加1。而出栈操作则是将top指向的元素存入临时变量,并将top值减1。这两个操作都只涉及数组下标的变化,不涉及元素的实际移动或删除。
如何理解顺序栈与顺序表在structure上的相同性和不同性?
顺序栈和顺序表在structure上基本一致,都基于数组,top作为最后一个元素的下标。区别在于顺序栈仅对插入、删除等操作有限制,而顺序表则允许在任何位置进行插入、删除等操作。尽管概念上有所不同,但其核心结构相同,只是在具体操作函数上有差异。
在单链表中,如何通过赋值操作来实现指针的移动?
在单链表中,要实现指针Q的移动,可以使用赋值操作Q = Q->next。通过这种方式,每当循环条件满足时(即Q->next不为空),指针Q就会指向下一个节点,从而实现了指针的移动。这句话的意义在于,当需要在链表中查找或操作节点时,可以通过不断更新指针的指向来遍历整个链表。
在链表操作中,添加或删除尾部元素的时间复杂度为何较高?
在单链表操作中,由于链表的结构是箭头单向向后,要进行尾部元素的添加或删除操作时,需要找到该元素的前驱节点才能执行操作。由于不知道前驱节点的指针,找到并定位到该节点需要消耗时间ON,其中N代表链表中的节点数量。因此,在尾部进行元素的添加或删除操作相对耗时。
在单链表中如何解决指针丢失的问题?
在单链表操作中,为了避免因指针丢失而无法继续操作的问题,有两种解决方案。一是注意操作顺序,确保先创建好指向当前节点的临时指针;二是多花指针空间,预先声明一个指针指向当前节点,这样就可以顺利地进行操作。同时,在实际应用中,应提前准备好前驱节点以便进行删除操作。
如何利用链表进行括号匹配问题的判断?
在链表结构中,可以通过栈的逻辑来判断括号匹配问题。当遇到左括号时将其入栈,遇到右括号时则从栈顶取出一个左括号进行匹配判断。若匹配成功,则继续处理下一个字符;若不匹配或栈为空则表示存在不匹配的右括号。此外,为了存储括号信息,可以使用字符串作为数据结构,通过循环遍历字符串并检查每个字符是否符合括号匹配的原则,从而实现括号匹配的判定。
在做while循环时,如何处理括号?
在进行while循环时,遇到圆括号时直接入栈,遇到方括号时则需要从栈中弹出元素进行匹配。当栈中存在一个后括号但没有对应的前括号时,说明程序遇到不匹配状态,此时终止循环,并根据栈是否为空判断括号匹配情况。
如何利用栈判断表达式中的括号是否对称?
利用栈实现括号对称判断的原理是,当遇到左括号时入栈,遇到右括号时检查栈顶元素是否为左括号并出栈。整个过程中如果栈始终保持非空且最终栈为空,则表明括号对称匹配。
如何将其他场景应用到栈的操作中?
除了括号匹配,还可以将栈应用于进制转换等其他场景。例如,在转换八进制数时,可以将数字除以8并记录余数,余数倒着读出来,就是最终的转换结果。这一过程同样可以通过入栈、出栈等栈操作来实现。
计算机内部如何处理表达式求值?
计算机在内部处理表达式求值时,首先将中缀表达式转换为后缀表达式(逆波兰表达式),这样可以按照先出现的运算符优先进行计算。然后通过读取后缀表达式中的元素,遇到运算符时取出前面连续的两个元素进行运算,并将结果放回原位置,最终得到整个表达式的计算结果。
综合表达式法中,栈的作用是什么?
在综合表达式法中,栈主要起到存放运算对象和符号的作用。一个栈用来装运算对象(如2、4、3、6),另一个栈用来装符号(如加号、减号、乘号等)。通过这两个栈的操作,可以实现表达式的求解过程,特别是通过栈的先进后出特性来处理不同符号的优先级和入栈出栈顺序。
为什么前括号的优先级别在站外很高,而在站内会降低?
前括号在站外时,由于其高优先级别,可以迅速入栈,类似高个子直接跨过寺庙门槛。但为了保证后续符号也能顺利入栈,需要将前括号的优先级别在进入栈时降低,就像小孩通过降低门槛爬过门槛一样。这样,前括号在栈内优先级会降低,以便其他低优先级符号也能进入栈中参与运算。
如何利用栈实现表达式的求解?
首先,在表达式的字符串中加上特殊符号(如井号)以指示开始和结束。然后,通过循环遍历字符串中的每个字符。当遇到井号时,认为其为低优先级的“门槛”,可以直接入栈。接着,遇到运算对象时,不论其大小,都直接放入栈内。最后,根据当前栈顶符号与后续符号的优先级比较结果,决定是否将栈顶符号出栈并进行运算,然后再将运算结果重新入栈。整个过程遵循栈的先进后出特性,最终栈底元素就是整个表达式的求解结果。
栈在递归函数调用中的作用是什么?
在递归函数调用中,栈扮演着“指示器”的角色。每次函数调用时,都会将返回地址压入栈中,表示从当前函数返回后应继续执行的地方。当函数执行到return语句时,会从栈中弹出相应地址,让程序返回到之前的调用点继续执行。通过这种方式,栈确保了递归调用的正确执行顺序,同时也解决了函数内部调用链中的地址记录问题。
