妈妈说,生活就像一盒各种口味的巧克力,你永远不知道下一块是什么。

我说生活像这个棒棒糖。不同口味,方向相反的味道一路走一路相伴,衰老和成长缠绕在一起,成了最终的滋味。

一、 卷积的直觉
这一生,从某一时刻开始,你探索世界,
随着时间的增长,你经历的新鲜事越来越少
10岁,你充满好奇,事事新鲜,经历4件新鲜事,
20岁,你充满憧憬,经历了3件新鲜事,
30岁,你带着希望,经历了2件新鲜事,
40岁,你百无聊赖,经历了1件新鲜事.
但随着时间的增长,你所经历的新鲜事沉淀出的智慧将逐次增高。每经过10年沉淀,都会带来更高层次的收获
10岁时,你看到一个新鲜事,对它不是很了解,这件事带给你1分的智慧
20岁时,你从书中读到它,似乎有所感悟,它给你带来2分的智慧。
30岁时,你在生活中经历了它,切身体会,它给你带来3分的智慧。
40岁时,你在别人的生活中读到了它,感同身受,它给你带来4分的智慧
年龄阶段的增长(1,2,3,4)
每隔10年经历的新鲜事f->(4,3,2,1)
每隔10年新鲜事带来的收获g->(1,2,3,4.)
要想让智慧通过人生与经历相遇,它们的方向必须相向而行,就像一列火车必须反转车头才能通过隧道。
所以我们将g反转为g(-u)(蓝色部分),按40岁来算,平移将g的“车头”停留在隧道f起始入口
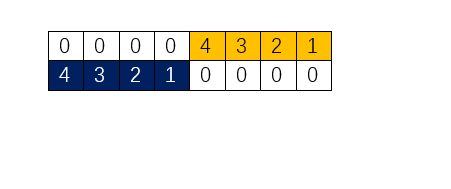
并将g逐次向前平移,模拟年龄阶段递增
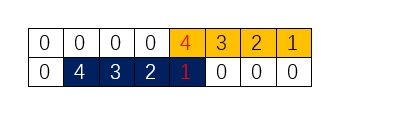
10岁时,你经历4件新鲜事,每件事带来1分的智慧。你的智慧点数=4*1
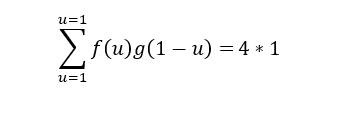
再向前,模拟20岁
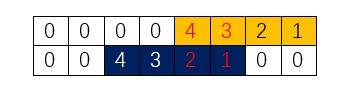
20岁时,10岁时经历的4件新鲜事智慧点数沉淀为2,而你又经历了3件新鲜事,初次体味,它们给你带来1分智慧,此时你的智慧分数为:4*2+3*1
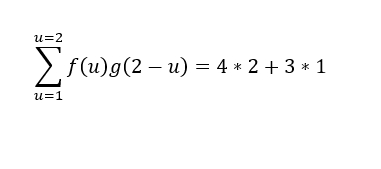
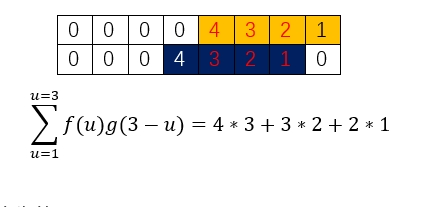
以此类推
30岁时,你的智慧分数:4*3+3*2+2*1
40岁时,你的智慧分数:4*4+3*3+2*2+1*1
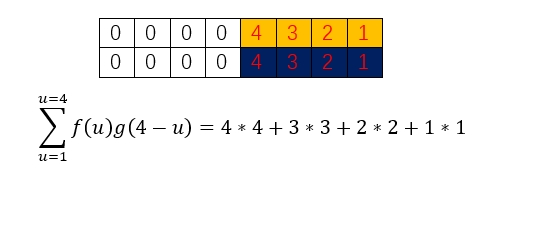
就是一种卷积的一种直觉,相反方向的两个函数,一个退,一个增,乘积求和,好像某种缠绕。
我们可以预测,某个年龄段t,它所经历的智慧点数为
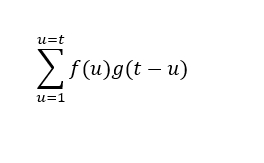
二、信号处理中的卷积
信号处理中的卷积,往往用以下公式表示
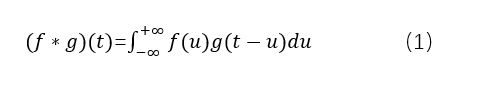
这时函数是连续的,用积分代表求和。
根据以上的理解,我们可以把上述过程看成,g反转后和f以相反的方向,逐次相交乘积,并最终求和的过程。而变量“t”,指示两个函数相交的程度,或者说,是g向前平移的程度。
我们用一组图来说明这个过程:
假设,函数f(u)的图像如下图所示

函数g(u)的图像如下图所示:
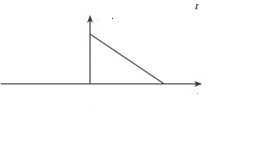
将g(u)反转为g(-u)
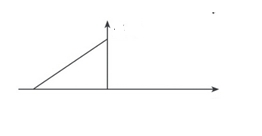
g(-u)不断向前平移,再某一时刻t,g(t-u)和f(u)相交
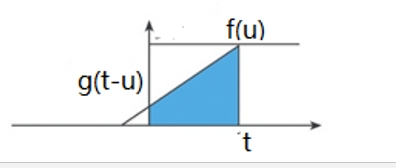
取乘积后求积分形成基于t变化的卷积函数
三、图像中的卷积
不管从直觉分析,还是从信号处理的角度,我们都看到,卷积实际上就是两个函数交叉相乘而求和的过程。
那么图像处理中的卷积,又是什么呢。
对,同样是交叉相乘,求和。
只不过,因为图像在计算机中,表示为二维矩阵,此时的函数乘积,变为二维矩阵的元素乘积。
所谓交叉相乘,变成镜像位置元素相乘。
一个图像是一个很大二维矩阵,通常,我们定义一个小矩阵,作为模板窗口,在图像上滑动,求卷积,以求得图像在某个位置的特征,这个模板窗口就是卷积核。
卷积核,有时也称为算子。通常根据不同的算子,可以取得图像某一位置不同方面的特征。比如sobel算子和lapacian算子,可以取得图像的轮廓特征
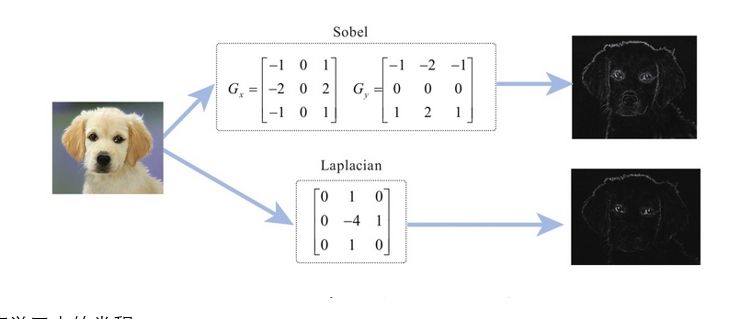
一个二维的图像
,卷积核为
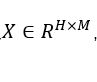
,通常k为奇数。图像通过卷积核计算输出:
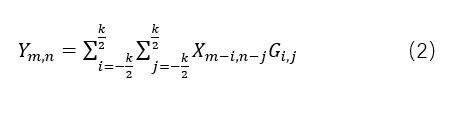
四、深度学习中的卷积。
深度学习中的卷积,和图像处理中的卷积相似,但稍有不同。
我们了解到,不论在信号处理,还是图像处理中,卷积的乘积都是交叉进行的。所以在上述图像处理中,我们必须对卷积核进行翻转再与图像局部区域各个相应元素相乘。
而深度学习中,卷积核不需要进行翻转。
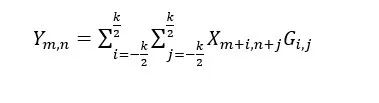
注意到上述公式和公式(2)区别,仅在于图像X的位置计算不同。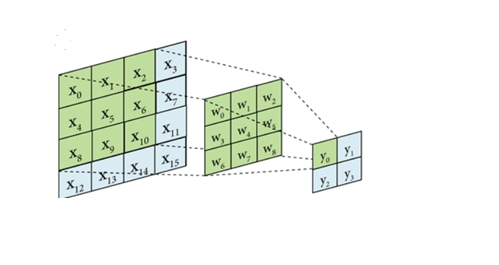
注意到上图,左边是原图像,中间是卷积核,右边是输出。
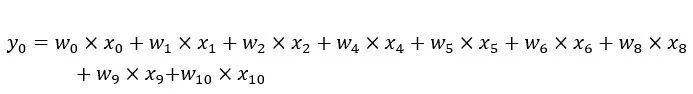
每个卷积核提取某种特征,为了增加特征的丰富程度,我们常会使用多个卷积核。最后将输入与每个卷积核得到的结果拼接起来,得到一个feature map。
可见,feature map是个 3维的张量。
五:池化
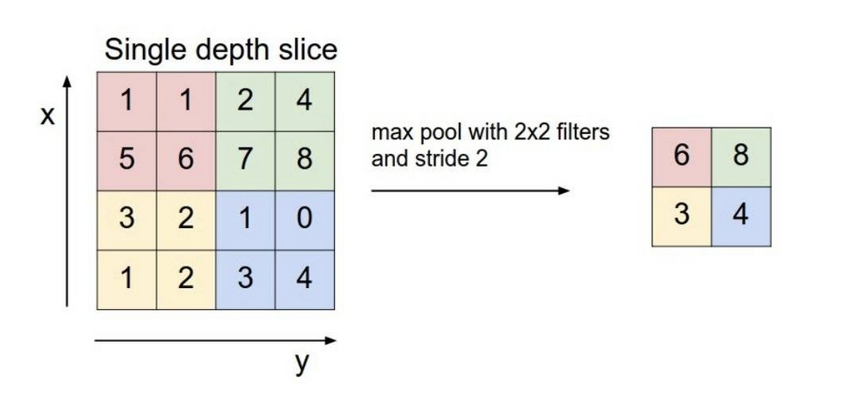
用各种卷积核滑动于图像之上,做卷积运算输出特征后,可以进一步都这些特征“采样”,从而缩小feature map大小,减少计算量。
通常我们将输入的图像划为若干个区域,只需采样该区域的最大值或平均值进行输出。
六:卷积神经网络
卷积神经网络,就是将卷积层于池化层堆叠得到的。
很有名的AlexNet,由5个卷积层,2个池化层,和3个全连接层组成。
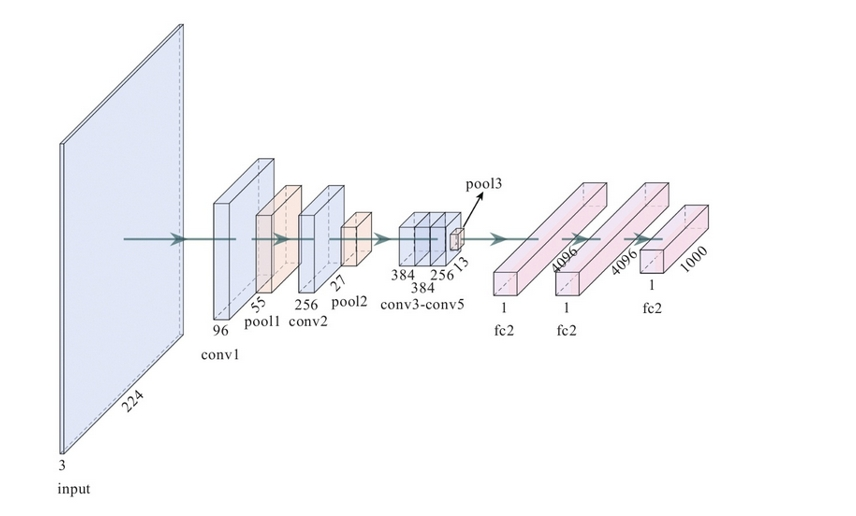
第一层:卷积层,卷积核大小11*11,96个卷积核,输出96个特征图。
第二层:池化层,采用最大值池化,池化窗口为3*3
第三层:卷积层,卷积核大小5*5,256个卷积核。
第四层:池化层,采用最大值池化,池化窗口为3*3
第五-七层:卷积层,卷积核第五层384个,第六层384个,第七层256个,卷积核大小3*3
最后三层:全连接层。
七:卷积网络的神奇特征
卷积网络有个很神奇的特征。就是因为它是卷积层堆叠而成,而我们知道,卷积实质是某种特征提取,这中卷积层的堆叠,使我们在每一层可以提取不同层次的特征。
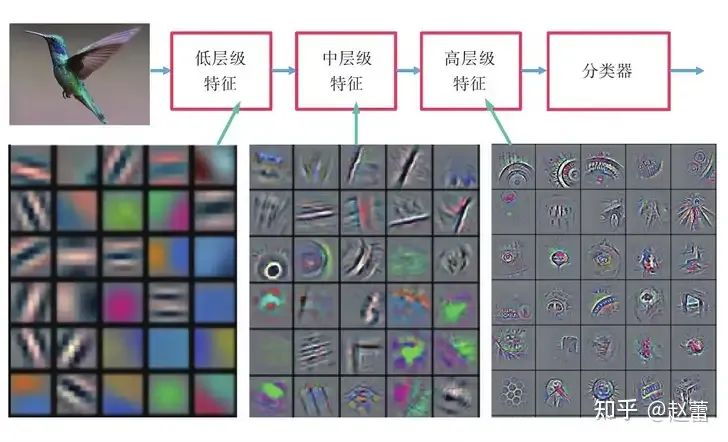
其中低层次的特征比如颜色,边角;中等层次的特征比如图像纹理,高层次特征比如图像语义。
以下是一个CNN可视化工具,动动鼠标,感受一下!
https://poloclub.github.io/cnn-explainer/
