问题描述
中国古代数学家张丘建在他的《算经》中提出了一个著名的“百钱百鸡问题”:一只公鸡值五钱,一只母鸡值三钱,三只小鸡值一钱,现在要用百钱买百鸡,请问公鸡、母鸡、小鸡各多少只?

问题分析
用百钱如果只买公鸡,最多可以买20只,但题目要求买100只,由此可知,所买公鸡的数量肯定在0~20之间。同理,母鸡的数量在0~33之间。在此不妨把公鸡、母鸡和小鸡的数量分别设为cock、hen、chicken,则cock+hen+chicken=100,因此百钱买百鸡问题就转化成解不定方程组的问题。
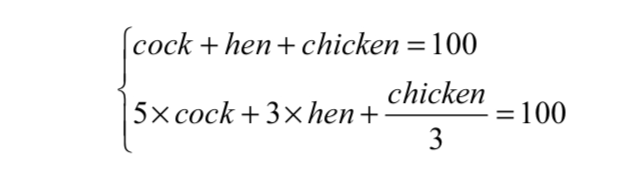
解题过程
我们可以通过穷举法解决这个问题,尝试不同的公鸡 cock 和母鸡 hen 的数量,计算出相应的小鸡 chicken,并检查是否满足总和为 100 只鸡和 100 钱。
# 遍历公鸡和母鸡的可能数量
def hundred_chickens():solutions = []for cock in range(21): # 公鸡最多买20只,因为100 / 5 = 20for hen in range(34): # 母鸡最多买33只,因为100 / 3 = 33chicken = 100 - cock - hen # 小鸡数量if chicken % 3 == 0 and 5 * cock + 3 * hen + chicken // 3 == 100: # 小鸡数量必须是3的倍数,且总花费为100钱solutions.append((cock, hen, chicken))return solutions# 打印所有可能的解决方案
results = hundred_chickens()
for solution in results:print(f"公鸡: {solution[0]} 只, 母鸡: {solution[1]} 只, 小鸡: {solution[2]} 只")
代码解释:
- 公鸡遍历:公鸡
cock的数量最多为 20 只,因为一只公鸡 5 钱,若买 21 只就会超过 100 钱。- 母鸡遍历:母鸡
hen的数量最多为 33 只,因为一只母鸡 3 钱,若买 34 只就会超过 100 钱。- 小鸡计算:每次尝试公鸡和母鸡的组合,剩下的鸡的数量为
chicken= 100 -cock-hen,并且小鸡的数量chicken必须是 3 的倍数。- 条件检查:检查是否满足总钱数为 100 钱,即 5*
cock+3*hen+chicken/3=100。
结果输出
运行代码后,所有的解法为:
公鸡: 0 只, 母鸡: 25 只, 小鸡: 75 只
公鸡: 4 只, 母鸡: 18 只, 小鸡: 78 只
公鸡: 8 只, 母鸡: 11 只, 小鸡: 81 只
公鸡: 12 只, 母鸡: 4 只, 小鸡: 84 只
总结
通过遍历所有的公鸡和母鸡的数量组合,计算相应的小鸡数量并检查是否满足题目中的条件,我们得到了四组符合条件的答案。
