独立同分布的中心极限定理:
设 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn 是独立同分布的随机变量序列,且 E ( X i ) = μ E(X_i) = \mu E(Xi)=μ, D ( X i ) = σ 2 > 0 D(X_i) = \sigma^2 > 0 D(Xi)=σ2>0,则随机变量之和 ∑ i = 1 n X i \sum_{i=1}^{n}X_i ∑i=1nXi 的标准化变量 ∑ i = 1 n X i − n μ n σ \frac{\sum_{i=1}^{n}X_i - n\mu}{\sqrt{n}\sigma} nσ∑i=1nXi−nμ 的分布函数 F n ( x ) F_n(x) Fn(x) 对于任意 x x x 满足 lim n → ∞ F n ( x ) = Φ ( x ) \lim_{{n \to \infty}} F_n(x) = \Phi(x) limn→∞Fn(x)=Φ(x),其中 Φ ( x ) \Phi(x) Φ(x) 是标准正态分布的分布函数。
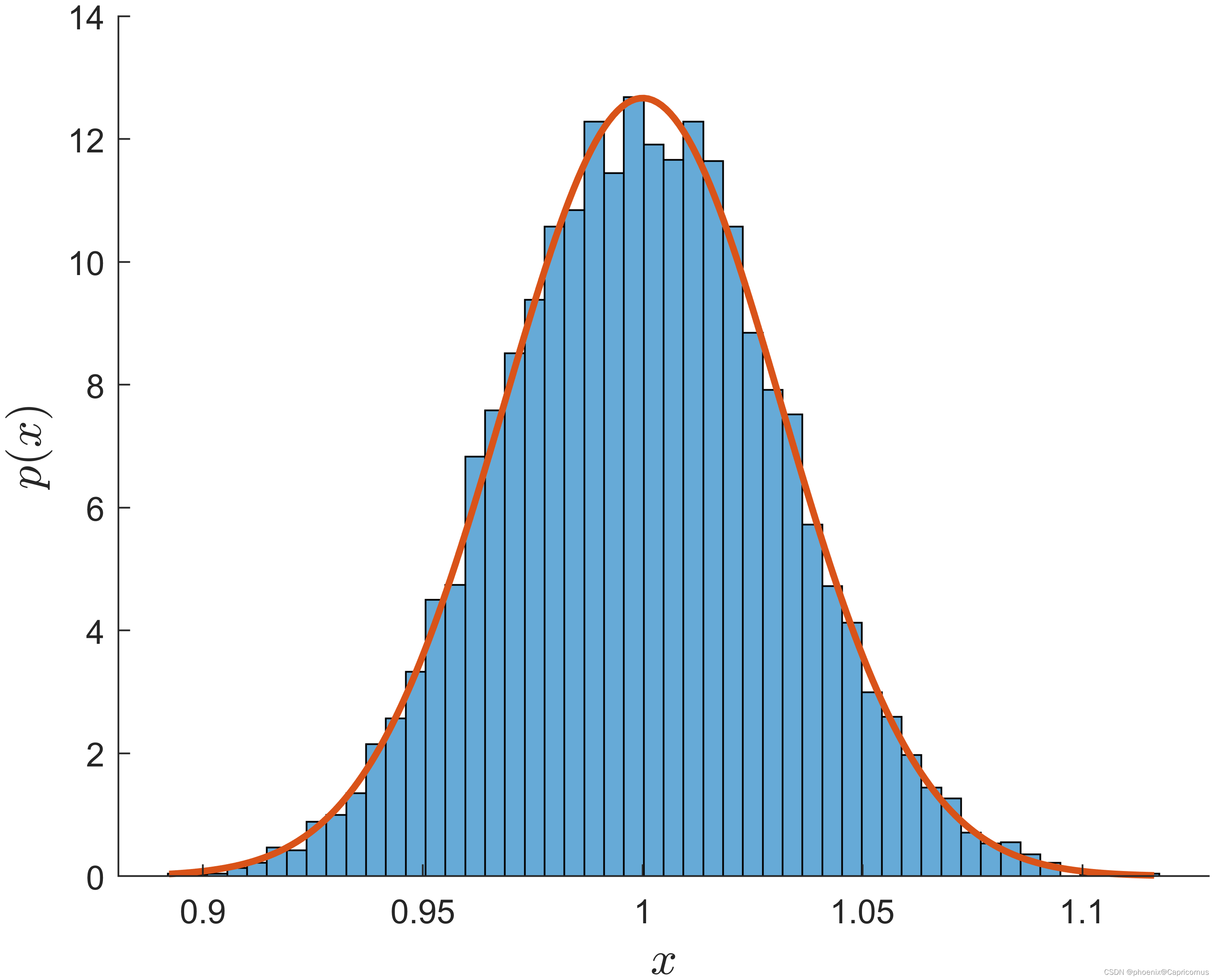
简单来说,中心极限定理表明,当从任意一个总体中抽取样本量足够大的样本时,样本均值的分布将趋近于正态分布,无论原来的总体分布是什么。
mu = 1; % Population parameter
n = 1e3; % Sample size
ns = 1e4; % Number of samples
%%
rng('default') % For reproducibility
samples = exprnd(mu,n,ns); % Population samples
means = mean(samples); % Sample means
%%
[muHat,sigmaHat] = normfit(means);
numbins = 50;
%%
figure
histogram(means,numbins,'Normalization','pdf')
hold on
x = min(means):0.001:max(means);
y = normpdf(x,muHat,sigmaHat);
plot(x,y,'LineWidth',2)
box off
xlabel('$x$', 'FontSize',14, 'Interpreter','latex')
ylabel('$p(x)$', 'FontSize',14, 'Interpreter','latex')