MFCC C++实现与Python库对比
MFCC理论基础
在音频、语音信号处理领域,我们需要将信号转换成对应的语谱图(spectrogram),将语谱图上的数据作为信号的特征。语谱图的横轴x为时间,纵轴y为频率,(x,y)对应的数值代表在时间x时频率y的幅值。通常的语谱图其频率是线性分布的,但是人耳对频率的感受是对数的(logarithmic),即对低频段的变化敏感,对高频段的变化迟钝,所以线性分布的语谱图显然在特征提取上会出现“特征不够有用的情况”,因此梅尔语谱图应运而生。梅尔语谱图的纵轴频率和原频率经过如下公式互换:
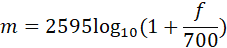
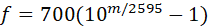
其中f代表原本的频率,m代表转换后的梅尔频率,显然,当f很大时,m的变化趋于平缓。而梅尔倒频系数(MFCCs)是在得到梅尔语谱图之后进行余弦变换(DCT,一种类似于傅里叶变换的线性变换),然后取其中一部分系数即可。
信号预加重(pre-emphasis)
通常来讲语音/音频信号的高频分量强度较小,低频分量强度较大,信号预加重就是让信号通过一个高通滤波器,让信号的高低频分量的强度不至于相差太多。在时域中,对信号x[n]作如下操作:
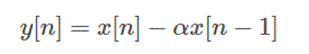
a通常取一个很接近1的值,typical value为0.97或0.95。从时域公式来看,这是一个高通滤波器,我们从z变换的角度看一下滤波器的transfer function:
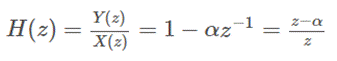
可以看出滤波器有一个极点0,和一个零点a。当频率为0时,z=1, 放大系数为(1-a)。当频率渐渐增大,放大系数不断变大,当频率到pi时,放大系数为(1+a)。离散域中,[0,pi]对应连续域中的0, fs/2。其中fs为采样率,在我们这里是44.1kHz。因此当频率到22000Hz时,放大系数为(1+a)
分帧(framing)
预处理完信号之后,要把原信号按时间分成若干个小块,一块就叫一帧(frame)。为啥要做这一步?因为原信号覆盖的时间太长,用它整个来做FFT,我们只能得到信号频率和强度的关系,而失去了时间信息。我们想要得到频率随时间变化的关系,所以将原信号分成若干帧,对每一帧作FFT(又称为短时FFT,因为我们只取了一小段时间),然后将得到的结果按照时间顺序拼接起来。这就是语谱图(spectrogram)的原理。
加窗(window)
分帧完毕之后,对每一帧加一个窗函数,以获得较好的旁瓣下降幅度。通常使用hamming window。为什么需要加窗?要注意,即使我们什么都不加,在分帧的这个过程中也相当于给信号加了矩形窗,学过离散滤波器设计的人应该知道,矩形窗的频谱有很大的旁瓣,时域中将窗函数和原函数相乘,相当于频域的卷积,矩形窗函数和原函数卷积之后,由于旁瓣很大,会造成原信号和加窗之后的对应部分的频谱相差很大,这就是频谱泄露。hamming window有较小的旁瓣,造成的spectral leakage也就较小。其中hamming window函数如下:
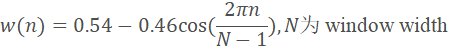
加窗分帧过程,实际是在时域上使用一个窗函数和原始信号进行相乘:
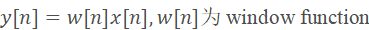
快速傅里叶变换(FFT)与能量谱(Power spectrum):
使用FFT的目的是将时域信号转换到频域。通过计算FFT结果的模平方实现信号的功率谱密度估计。其中平方实际对应二阶能量计算,目的是为了增强语音信号的特征表示,使MFCC对语音信号的特征更加敏感。
对于每一帧的加窗信号,进行N点FFT变换,也称短时傅里叶变换(STFT),N通常取256或512,然后用如下的公式计算能量谱:
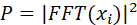
其中二阶能量计算可表示为:
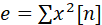
梅尔滤波器组与Filter Banks特征:
Mel刻度,这是一个能模拟人耳接收声音规律的刻度,人耳在接收声音时呈现非线性状态,对高频的更不敏感,因此Mel刻度在低频区分辨度较高,在高频区分辨度较低,与频率之间的换算关系为:
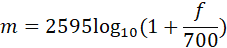
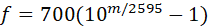
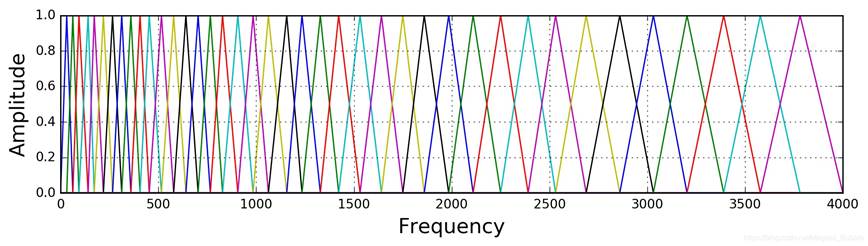
Mel滤波器组就是一系列的三角形滤波器,通常有40个或80个,在中心频率点响应值为1,在两边的滤波器中心点衰减到0,如下图所示:
具体公式表示为:
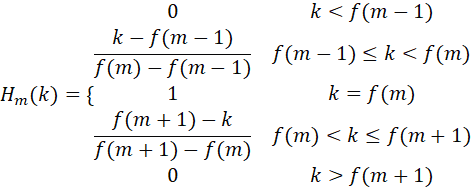
最后在能量谱上应用Mel滤波器组,其公式为:
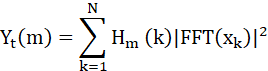
取对数得到log mel-filter bank:
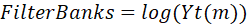
最后,根据以上描述,我们可以将Filter Banks特征分为以下几个步骤:
(1)确定滤波器组个数P
(2)根据采样率fs,DFT点数N,滤波器个数P,在梅尔域上等间隔的产生每个滤波器的起始频率和截止频率。
(3)将梅尔域上每个三角滤波器的起始、截止频率转换线性频率域,并对DFT之后的谱特征进行滤波,得到P个滤波器组能量,进行log操作,得到FBank特征。
离散余弦变换DCT与MFCC特征:
MFCC特征是在FBank特征的基础上继续进行离散余弦变换(DCT)变换。提取到的FBank特征,往往是高度相关的。因此可以继续用DCT变换,将这些相关的滤波器组系数进行压缩。通常取13维,扔掉的信息里面包含滤波器组系数快速变化部分。
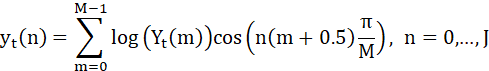
C++实现
· 采用C++实现了MFCC算法,包括预加重滤波器、应用汉明窗、FFT、能量谱计算、Mel滤波器组特征提取以及DCT变换等核心功能。整体流程如下:
----------------------------初始化--------------------------
main.cpp(main)-> //入口函数,接收外部参数
mfcc.cpp(class MFCC)-> //初始化
--------------------------开始处理--------------------------
mfcc.cpp(process)-> //分帧
mfcc.cpp(processFrame)-> //处理单个窗口
mfcc.cpp(preEmphHam)-> //加汉明窗
mfcc.cpp(fft)-> //快速傅里叶变换
mfcc.cpp(computePowerSpec)-> //计算能量谱
mfcc.cpp(applymelFilterBanks)-> //提取Log Mel Filter Bank
mfcc.cpp(applyDct)-> //使用Dct将Log Mel Filter Bank转为MFCC
--------------------------保存结果--------------------------
mfcc.cpp(v_d_to_string) //保存
Python与C++的对比实现与可视化评估
o 我们对C++实现的MFCC算法进行了性能优化,确保了算法的高效运行,特别是在处理大规模数据集时。然后,为了验证C++实现的正确性,使用Python的librosa和torchaudio库进行了实现用于对比,并利用python_speech_features库作为额外的参考。最后,我们使用Matplotlib对MFCC特征进行了可视化展示,包括不同库实现的MFCC特征曲线对比,以及C++实现与Python实现的一致性验证。
特征一、二:
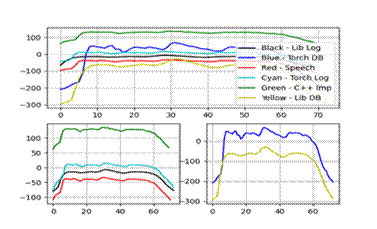
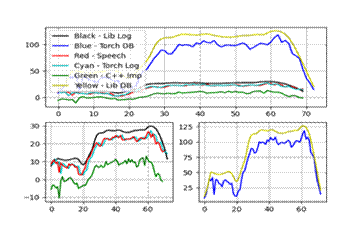
特征三、四:
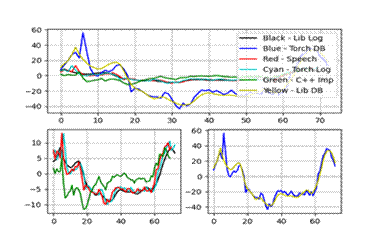
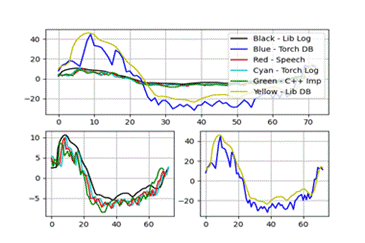
特征五、六:
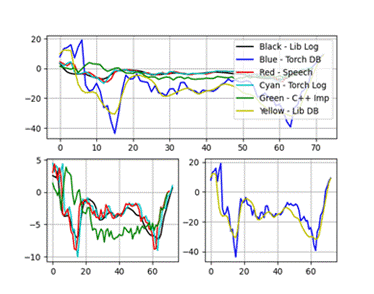
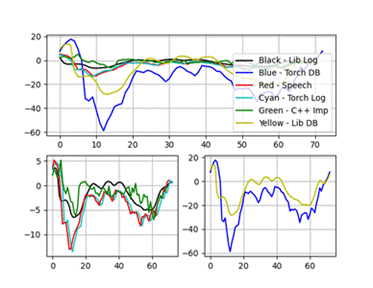
实验结果显示,C++实现的MFCC特征与Python库(如librosa和torchaudio)的结果在趋势上基本一致,但在数值上存在微小差异,这主要归因于不同库在归一化和数值精度处理上的差异。
结论:
本项目成功实现了MFCC特征提取算法的C++版本,并通过与其他流行库的对比验证了其准确性和有效性。C++实现在性能上显示出优势,尤其是在大规模数据处理上。此外,通过可视化评估,进一步证实了C++实现的MFCC特征与其他实现的一致性。
完整代码请访问github:CV-LS/mfcc_cpp_python (github.com)
如果您觉得这个项目对您有所帮助,请考虑给它一个星标(star)或 fork。您的支持是我们持续改进和发展的动力。
