接上一篇,前两篇讲完了关于二叉树的基础知识以及二叉树的顺序存储结构——堆,今天我们来了解一下二叉树的第二种存储结构——链式存储结构,同样,有了之前链表的基础,我们在理解这个结构的时候也会更加轻松。
链式二叉树
用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址,其结构如下:
//定义一个二叉树的结构
typedef char BTDatatype;
typedef struct BinaryTreeNode
{BTDatatype data;struct BiNaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;有了对于这个结构的初步认知,我们现在就可以尝试手动来构建一棵二叉树,和之前链表的一些操作一样,这里同样是动态开辟空间:
BTNode* BTbuyNode(BTDatatype x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return 1;}node->data = x;node->left = node->right = NULL;
}BTNode* CreatTree()
{BTNode* nodeA = BTbuyNode('A');BTNode* nodeB = BTbuyNode('B');BTNode* nodeC = BTbuyNode('C');BTNode* nodeD = BTbuyNode('D');BTNode* nodeE = BTbuyNode('E');BTNode* nodeF = BTbuyNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeB->right = nodeE;nodeC->left = nodeF;return nodeA;
}回顾二叉树的概念,二叉树分为空树和非空二叉树,非空二叉树由根结点、根结点的左子树、根结点的右子树组成的
而根结点的左子树和右子树分别又是由子树结点、子树结点的左子树、子树结点的右子树组成的,因此二叉树定义是递归式的,接下来就一起来欣赏递归的暴力美学吧!
链式二叉树的实现与基本操作
这里涉及到的知识相比于其他数据结构要更多、更复杂一些因为涉及到很多递归的知识,代码虽然简单,但是思路要理解起来可能会比较困难,但是没关系,博主这里会以最详细的语言、图文并茂地为大家解释清楚其中的思路!
二叉树的前、中、后序遍历
先来一道开胃小菜,二叉树的前序遍历,所谓前序,意思就是 根 -> 左 -> 右 这样一个顺序对二树的数据进行遍历,那具体的流程是怎样的呢,我给大家画个图:
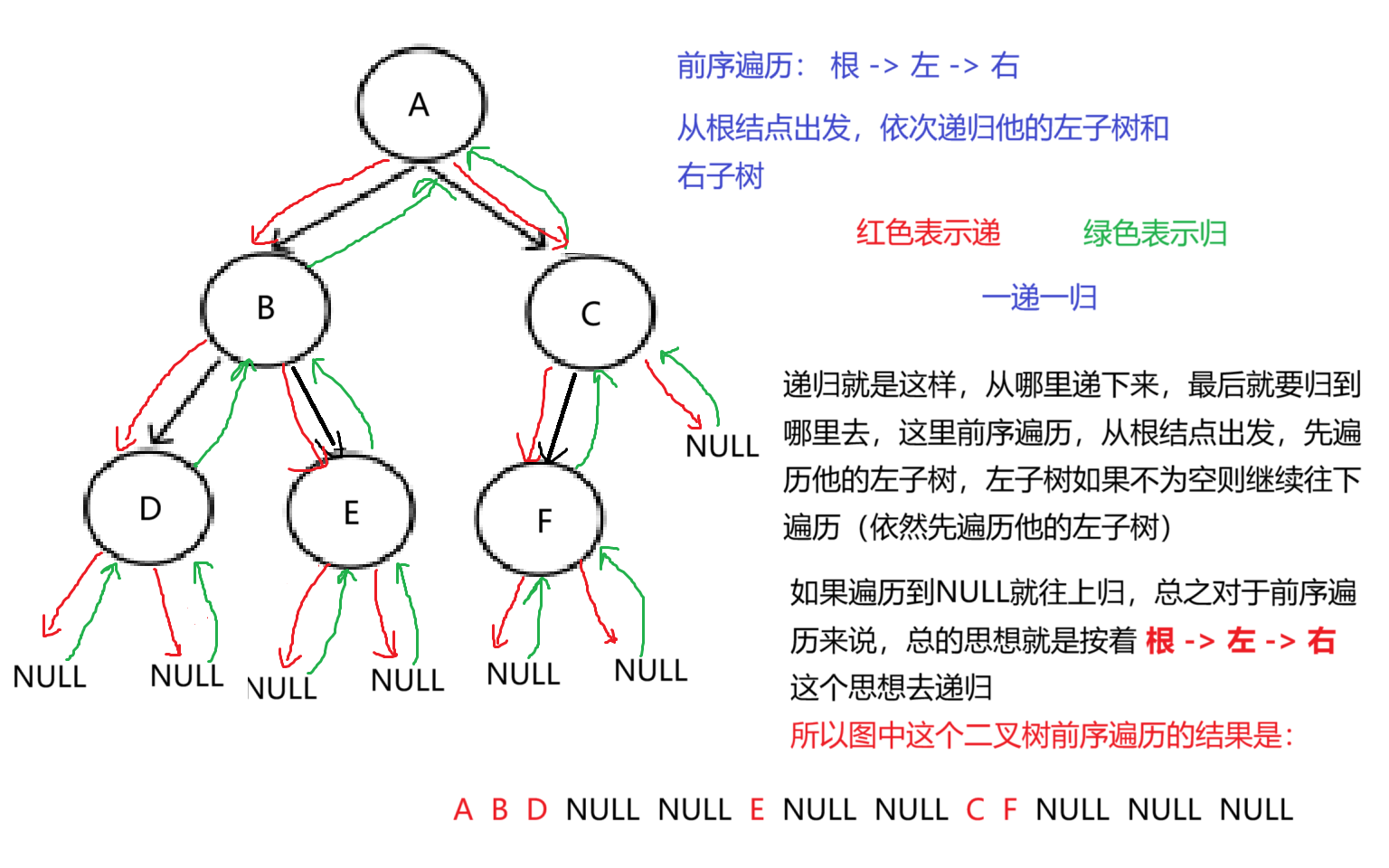
这就是前序遍历的过程,接下来我们上代码,配合着代码来让大家感受一下递归的美学:
//前序遍历
void PreOrder(BTNode* node)
{if (node == NULL){printf("NULL ");return;}printf("%c ", node->data);PreOrder(node->left);PreOrder(node->right);
}看,代码很简单吧,总共不超过 10 行代码就搞定了
我依然通过代码再给大家画个图:

这个图看起来有点乱,因为有点小,右边的稍微清晰一点,可以重点看,主要就是想通过这张图给大家看一看递归的代码到底该怎么理解,从哪一句执行到哪一句,不至于蒙圈。
我相信大家现在应该是心里都有点感觉了,所以其实中序遍历和后序遍历的思想都和这个异曲同工,只不过一个按照 左 -> 根 -> 右 ,一个按照 左 -> 右 -> 根 的顺序而已,如果真正理解了上面这个前序遍历,那理解其他两个也不会有问题的~所以我就直接给大家上代码了!
//中序遍历
void MidOrder(BTNode* node)
{if (node == NULL){printf("NULL ");return;}PreOrder(node->left);printf("%c ", node->data);PreOrder(node->right);
}//后序遍历
void BackOrder(BTNode* node)
{if (node == NULL){printf("NULL ");return;}PreOrder(node->left);PreOrder(node->right);printf("%c ", node->data);
}大家也可以自己尝试去画画图,有不懂的也可以私信博主~
二叉树结点的个数
这个相比于之前的遍历可能会更有难度,但有了刚刚递归的基础,我相信大家也可以弄懂的!直接上图:

看得懂吗,是不是有点蒙蒙的,没关系,我再给你配上代码你就会明白了!
//求二叉树结点个数
int BTSize(BTNode* node)
{if (node == NULL){return 0;}return 1 + BTSize(node->left) + BTSize(node->right);
}只要遇到 NULL,我就返回一个 0,遇到的是一个结点,我就用 1 去加上他后续的递归,类似于一个累加的效果,思路就是这样,现在是不是有点感觉啦~
求二叉树叶子结点的个数
前面是求二叉树结点的个数,那这里让你求叶子结点的个数难道就不会了?不可能啦!思路都是一样滴。
这里我就不给大家画图了,因为递归逻辑和上面那个几乎是一模一样的,我直接给大家上代码:
//二叉树叶子结点的个数
int BTLeafSize(BTNode* node)
{if (node == NULL){return 0;}if (node->left == NULL && node->right == NULL){return 1;}return BTLeafSize(node->left) + BTLeafSize(node->right);
}前面我们求结点个数,用的是这个:
return 1 + BTSize(node->left) + BTSize(node->right);现在我们求叶子结点,用这个:
return BTLeafSize(node->left) + BTLeafSize(node->right);区别不就在于,我们这里要求的是叶子结点的个数,而不是单纯的遇到一个结点我就累加,我们要先判断这个结点是不是叶子结点再进行操作,是叶子结点我们就返回 1(叶子结点的特点不就是没有子树了吗,所以只要判断当前结点是否左右子树均为 NULL 就好了),不是就返回 0,当然,NULL肯定也不是一个叶子结点,所以也是返回 0。
二叉树第k层的结点个数
怎么去求第 K 层的结点个数呢,其实从上面的题来看,不难发现,我们去求结点个数的时候,一个最大的核心,也是最容易想到的思路是什么——结点个数 = 左子树结点个数 + 右子树结点个数
那么这里也可以很自然想到:第k层结点个数 = 左子树第 K 层结点个数 + 右子树第 K 层结点个数
思路不就出来了?
我这里同样给大家画个图:

这里博主画图的时候不小心画错了一支(就是 E 那棵子树画到 C 后边去了),但毫无影响,思路和逻辑都是一样的,这里给大家上代码,大家看完代码之后给大家一起讲解:
//二叉树第k层的结点个数
int BTLevelKsize(BTNode* node, int k)
{if (node == NULL){return 0;}if (k == 1){return 1;}return BTLevelKsize(node->left, k - 1) + BTLevelKsize(node->right, k - 1);
}其实博主认为这个递归代码的最最精髓的地方在于这个 K 从上往下依次减一,从 3 减到 1 这个过程中的所有结点都是没有被计数的,只有在 K 被减到 1 的时候所对应的这层结点才是第 K 层结点,自然在这个第 K 层,也就是 K == 1 时,才 return 1; 如此递归上去,注意这里不是累加上去!!这里只返回第 K 层结点的个数,并不是把之前的结点数量相加。
二叉树的高度和深度
看到这个题,大家脑子里都在想什么呢?我猜应该是什么 return 1 + ... + ... 之类的吧哈哈哈哈,其实还真就是这么个思路,只不过我们这里要考虑一个问题就是:二叉树的高度是由什么决定的
二叉树的高度:树中结点的最大层次,既然是最大层次,那我们肯定要知道最大的层次在哪吧,二叉树,二叉二叉,总共就两叉,还不就是看左右两棵子树那棵更高咯
所以这里我们要做的一件事就是确认左右哪两棵树高,这里我直接给大家上图上代码,配合着给大家讲:
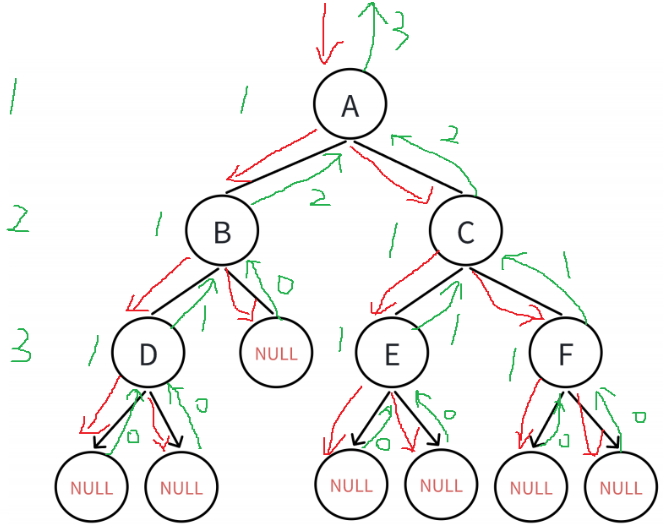
//二叉树的高度和深度
int BTDeepSize(BTNode* node)
{if (node == NULL){return 0;}int leftsize = BTDeepSize(node->left);int rightsize = BTDeepSize(node->right);return 1 + (leftsize > rightsize ? leftsize : rightsize);
}其实看这个代码可以看出来,左子树的高度经过递归最终累加到 leftsize 上,而右子树的高度经过递归最终累加到 rightsize 上,最终经过一个三目表达式:leftsize > rightsize ? leftsize : rightsize 来确定了哪棵子树才是最高的,并且归了回去。
二叉树查找值为x的结点
查找在这里思想其实更加简单,但是代码会比较难一点,我们这里也仍然是一个大核心:左、右
讲到这里插个嘴,二叉树这东西,你想想,他都已经是个二叉的树了,能在这个二叉树的递归里做文章的除了左右子树还能有谁,所以碰到关于二叉树的操作,尽量往左右子树这个方向去靠就对了
那么这里也是一样的,要查找值为 x 的结点,我们就分别去左右两棵子树去找就完事了,找到了就返回,没找到继续递归,就这么简单。
所以也是给大家上图上代码:

//二叉树查找值为x的结点
BTNode* BTFind(BTNode* node, BTDatatype x)
{if (node == NULL){return NULL;}if (node->data == x){return node;}BTNode* leftfind = BTFind(node->left, x);if (leftfind){return leftfind;}BTNode* rightfind = BTFind(node->right, x);if (rightfind){return rightfind;}return NULL;
}二叉树的销毁
二叉树的销毁就更简单了,大家看代码就能看会
递归左右子树,然后从下往上每个结点逐个逐个这么销毁就行啦
//二叉树的销毁
void BTDestroy(BTNode** node)
{if (node == NULL || *node == NULL){return;}BTDestroy(&((*node)->left));BTDestroy(&((*node)->right));free(*node);*node = NULL;
}二叉树的层序遍历
层序遍历的概念:
设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

如图所示,这是一棵普通的二叉树,他的层序遍历就是:A B C D E F
好了,了解了层序遍历是什么后,我们来尝试实现一下吧~
因为要实现层序遍历,所以这里如果我们按照前面递归的思想,从根结点出发,先递归他的左,再递归他的右,这样就是前序遍历了,无法实现层序遍历,我们要实现层序遍历,就要对于一个根结点来说,同时找到他的左和右才行,那这里怎么办呢?
这里我们借助队列这个数据结构来实现,大家看我接下来这张图的思路奥:

将结点的非空左右孩子入队列,入完之后取队头,出队,以上图为例,A 入队后,将 A 的左右孩子 B 和 C 入队,之后取队头(A),再将 A 出队,这时 B 就成了新的队头,C 依然还是在 B 的后面,再重复刚刚的操作,把 B 的非空左右孩子入队,此时就入了一个 D 跟在 C 的后面,再取队头(B),将 B 出队,这时 C 就成立新的队头,再将 C 的非空孩子,依次入队 E 和 F ,重复刚刚的操作,这样层序遍历就完成了~,有了思路,接下来我们就来尝试写代码咯!
//队列的初始化
void QueueInit(Queue* pq)
{assert(pq);//pq->size = 0;pq->phead = pq->ptail = NULL;
}//队列的销毁
void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;//pq->size = 0;
}//入队
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail!");exit(1);}newnode->data = x;newnode->next = NULL;if (pq->ptail == NULL)//如果队列当前为空{pq->phead = pq->ptail = newnode;newnode->next = NULL;}else{pq->ptail->next = newnode;pq->ptail = newnode;}//pq->size++;
}//出队
void QueuePop(Queue* pq)
{assert(!IsEmpty(pq));//if (pq->phead == NULL)//{// //perror("pq->phead == NULL");// return 1;//}if (pq->phead == pq->ptail){free(pq->phead);pq->phead = pq->ptail = NULL;}else{QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}//pq->size--;
}//取队头数据
QDataType QueueTop(Queue* pq)
{assert(!IsEmpty(pq));return pq->phead->data;
}//判断队列是否为空
bool IsEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL;
}//——————————先把队列的相关操作准备好———————————//二叉树的层序遍历
void LevelOrder(BTNode* node)
{Queue q;QueueInit(&q);QueuePush(&q, node);while (!IsEmpty(&q)){BTNode* top = QueueTop(&q);QueuePop(&q);printf("%c ", top->data);if (top->left)QueuePush(&q, top->left);if (top->right)QueuePush(&q, top->right);}QueueDestroy(&q);
}结尾
好了以上就是二叉树的所有内容了,下一章讲讲八大排序,敬请期待吧,觉得博客写的还不错的可以点点赞哦~
