成都装修公司前十名_企业网站建设要求_免费舆情网站下载大全最新版_石家庄网站建设

1. 函数秘密共享(FSS)定义  

        秘密共享是一种将一个值拆分为多个份额的方法，形式有多种，可以参考《安全多方计算(MPC)矩阵乘法算子的原理分析》。这里主要提及加法秘密共享，使得：这些份额可以重新组合以还原出秘密值；任意严格的份额子集都无法泄露秘密值的任何信息。使用方括号表示法来表示值 v 的第 i个秘密份额。使用 "+" 表示重新组合：。

        函数秘密【1，3】共享具有一个额外的要求，即可以在输入 x 上对函数 f 的份额进行计算，以得到 f(x) 的份额。给定，可以高效地计算出任意 x 对应的。使用  表示在输入 x上评估份额​。使用 "+" 表示重新组合：。

        对于函数 和  个评估者，函数秘密共享（Function Secret Sharing, FSS）通过以下（可能是随机的）算法来描述：

• Gen() → ()
  将函数分割成一组紧凑的秘密份额 ​。

• Eval() →
  使用秘密份额 和输入 x，输出 f(x) 的秘密份额 。

• Recover() → f(x)
  从 p 个秘密份额中恢复出 f(x)。

2. 为什么函数秘密共享（FSS）有用

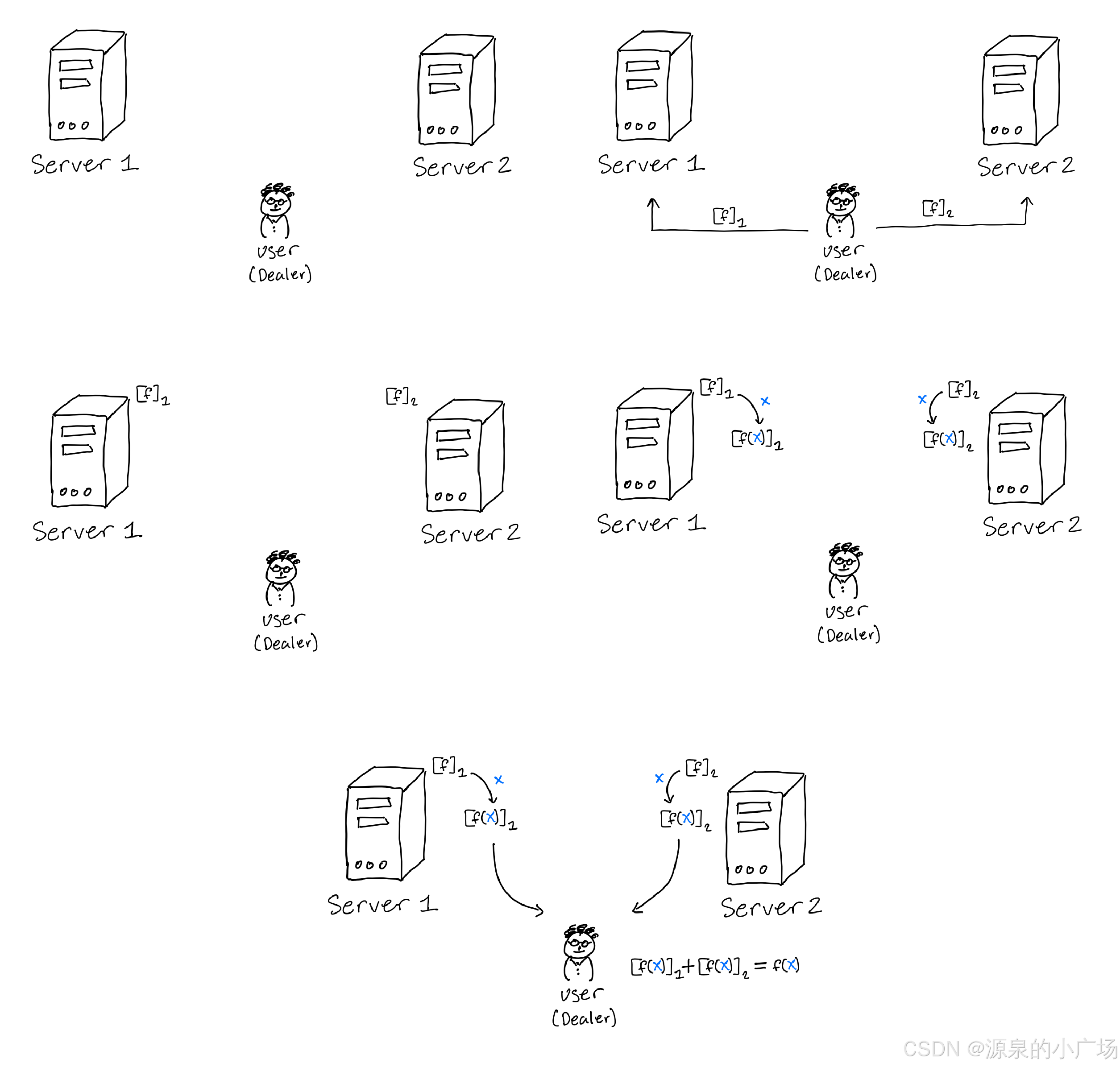
        假设一个客户端希望在云端存储的数据上运行某个函数，但不想将该函数暴露给云服务器，该怎么办？

解决方案：

假设服务器之间没有串通行为，并使用 FSS 来隐藏函数。

1. 客户端使用 FSS 将函数 f 进行秘密共享，分发给云服务器。
2. 云服务器在秘密共享的函数 f 上进行计算，并将（秘密共享的）结果 f(x) 返回给客户端。
3. 客户端在本地重新组合这些份额以获得 f(x)。

此外，FSS 在构建隐私保护系统中非常有用：

• 私密读取分布式数据库（私密信息检索）
  例如：在远程数据库上进行私密关键字搜索【2, 4】。

• 私密写入分布式数据库（私密信息写入）
  例如：匿名通信【5, 6, 7, 8】。

• 多方计算
  例如：为多方计算生成预处理（Silent OT extension）【9】。

3. FSS与DPF关系

        上述内容介绍了FSS ，其是一种通用的技术，用于将任意函数分割为多个秘密份额，使得这些份额能够在不泄露函数本身的情况下在分布式环境中进行计算。每个参与者持有函数的一部分份额，通过本地计算和通信，可以计算函数在某个输入值上的结果，并最终组合这些结果还原出函数的输出。

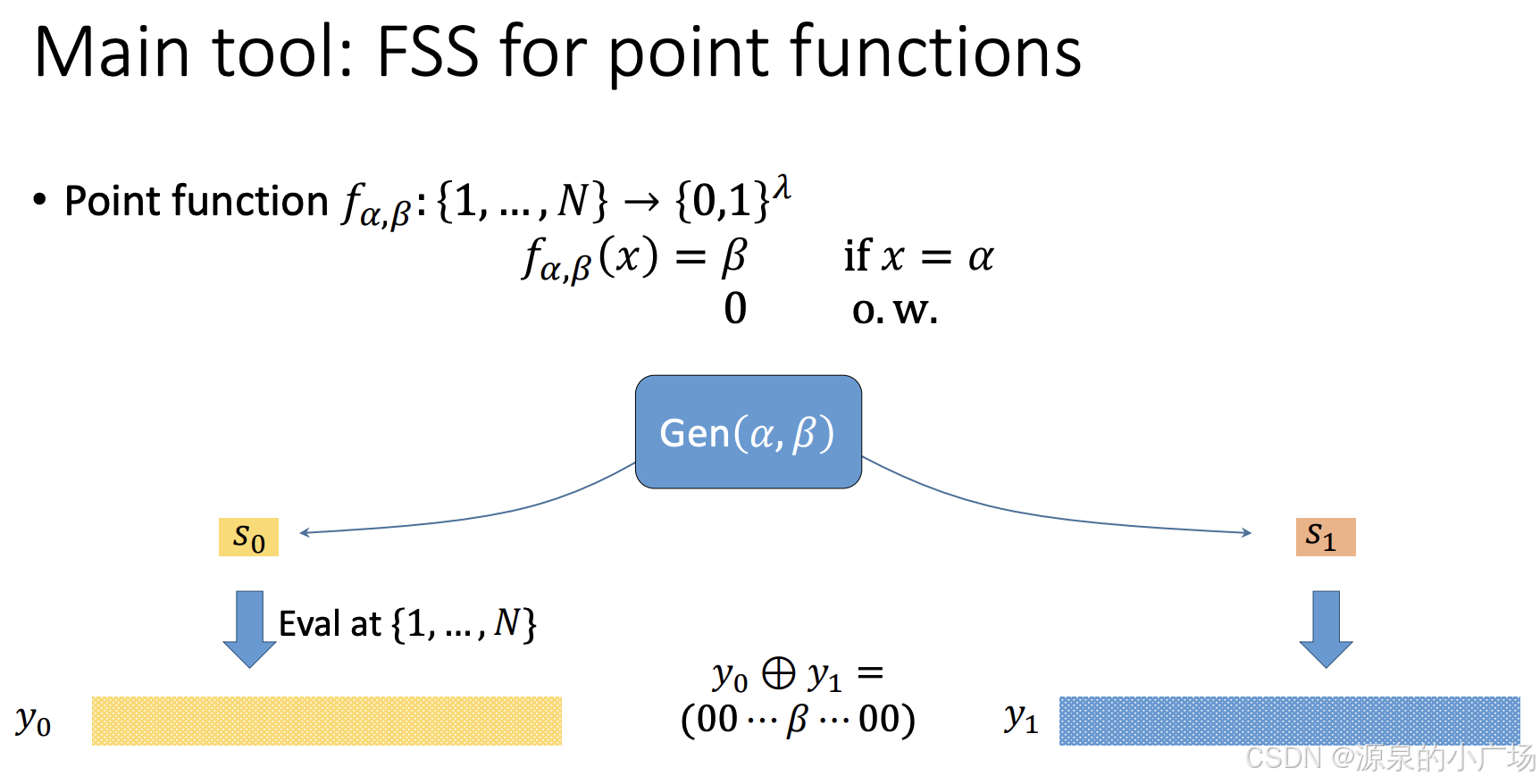
        而DPF（分布式点函数） 是 FSS 的一种特定形式，专门用于分享点函数。点函数是一种非常简单的函数，形式为：

        其中  是一个特定的输入值，v 是在 ​ 处的输出值。在 DPF 中，函数的秘密共享特别针对这种形式的点函数。DPF 可以让多个参与者在不泄露 和 v 的情况下对函数进行计算，并在需要时重新组合得到正确的点函数输出。由于点函数非常简单，DPF 通常有更高的效率和更小的计算开销，尤其适合需要查询特定位置或值的应用场景，如私密信息检索（PIR）等。

【10】中描述了PCG for tensor product from LPN and FSS过程。

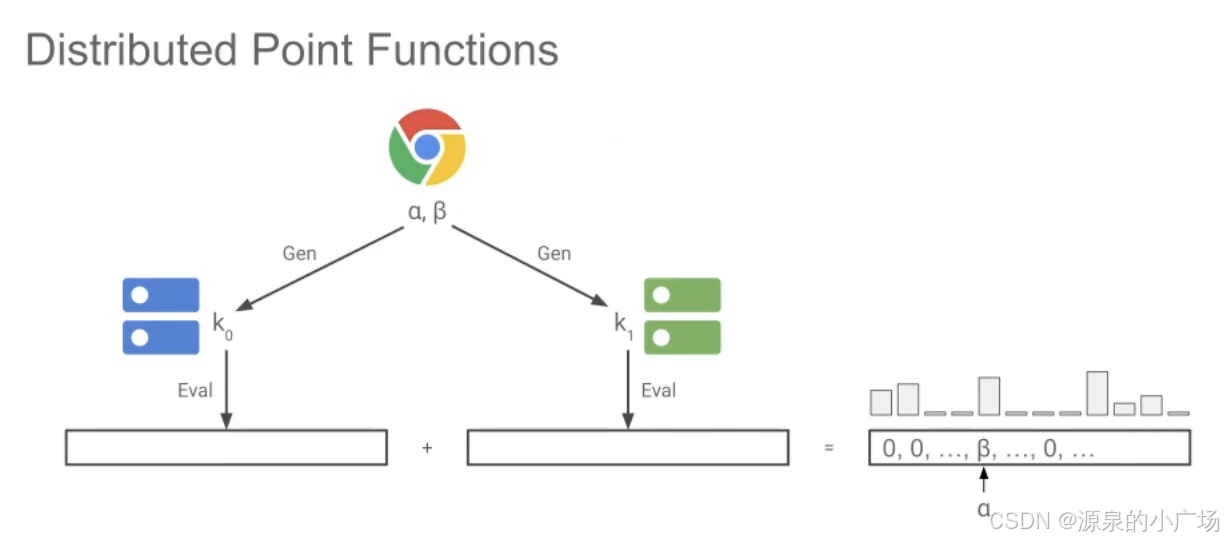
【11】中给出了基于DPF给出了多服务器PIR（私有信息检索）的解决方案。分布式点函数包含两个算法（Gen 和 Eval）：

• Gen(y) → ()：为 y 生成点函数的密钥
• Eval(, x') → y'：在输入 x 上评估点函数

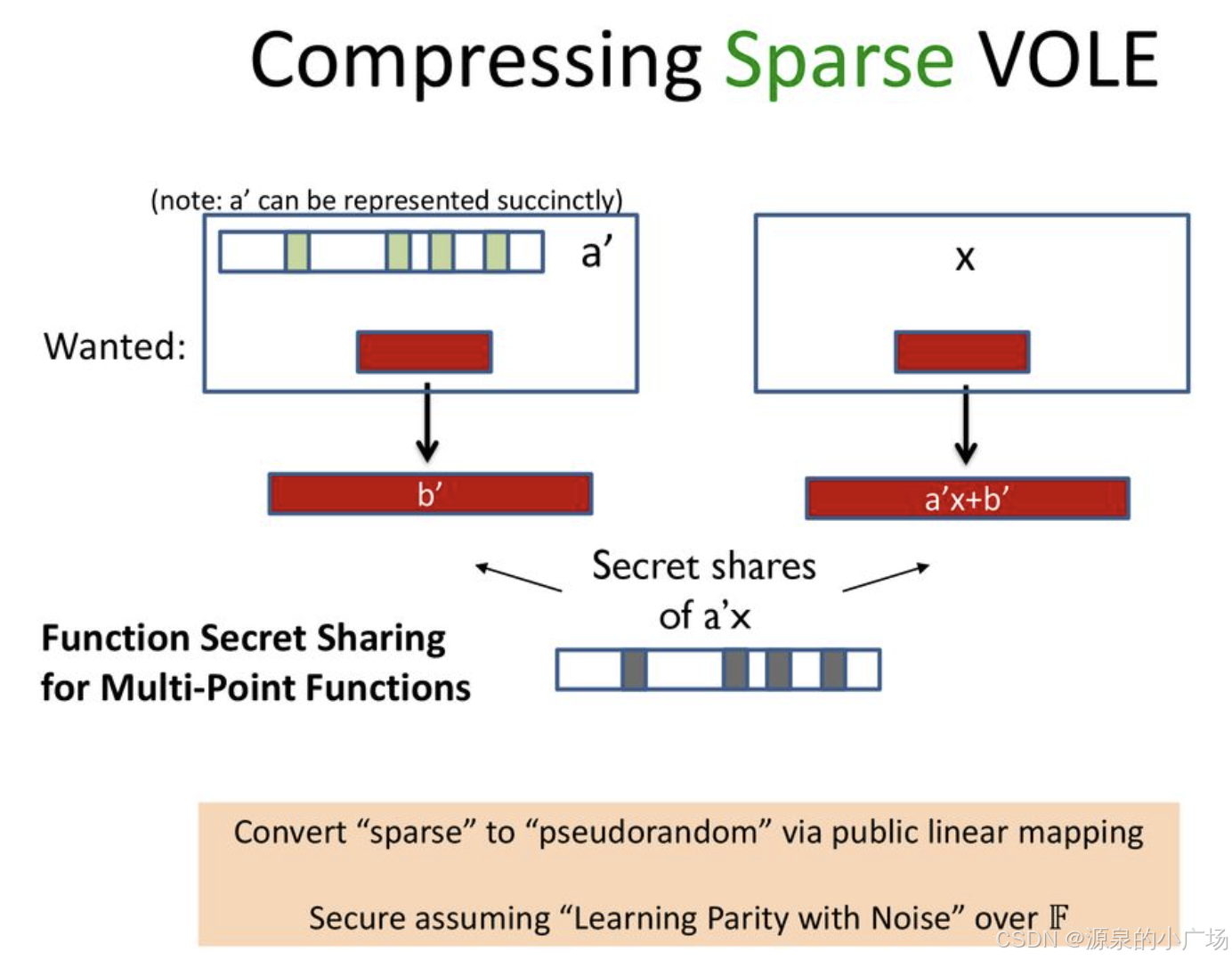
此外，【12】给出了FSS for Multi-point Funciton的应用

4. 参考材料

【1】Private Access Control for Function Secret Sharing

【2】Elette Boyle, Niv Gilboa, and Yuval Ishai. “Function secret sharing”. In: Annual international conference on the theory and applications of cryptographic techniques. Springer. 2015, pp. 337–367.

【3】Elette Boyle, Niv Gilboa, and Yuval Ishai. “Function secret sharing: Improvements and extensions”. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. 2016, pp. 1292–1303.

【4】Emma Dauterman et al. “DORY: An encrypted search system with distributed trust”. In: Proceedings of the 14th USENIX Conference on Operating Systems Design and Implementation. 2020, pp. 1101–1119.

【5】Henry Corrigan-Gibbs, Dan Boneh, and David Mazières. “Riposte: An anonymous messaging system handling millions of users”. In: 2015 IEEE Symposium on Security and Privacy. IEEE. 2015, pp. 321–338.

【6】Saba Eskandarian et al. “Express: Lowering the cost of metadata-hiding communication with cryptographic privacy”. In: 30th USENIX Security Symposium (USENIX Security 21). 2021, pp. 1775–1792.

【7】Adithya Vadapalli, Kyle Storrier, and Ryan Henry. “Sabre: Sender-anonymous messaging with fast audits”. In: 2022 IEEE Symposium on Security and Privacy (SP). IEEE. 2022, pp. 1953–1970.

【8】Zachary Newman, Sacha Servan-Schreiber, and Srinivas Devadas. “Spectrum: High-bandwidth Anonymous Broadcast”. In: 19th USENIX Symposium on Networked Systems Design and Implementation (NSDI 22). 2022, pp. 229–248.

【9】Elette Boyle et al. “Efficient pseudorandom correlation generators: Silent OT extension and more”. In: Annual International Cryptology Conference. Springer. 2019, pp. 489–518.

【10】Efficient Pseudorandom Correlation Generators: MPC with Silent Preprocessing

【11】Distributed Point Functions: Efficient Secure Aggregation and Beyond with Non-Colluding Servers

【12】Homomorphic Secret Sharing