宁波网络推广咨询_免费开源的cms_磁力搜索引擎下载_seo推广软件怎样

引言

大家好，我是GISer Liu😁，一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年9月学习赛的LeetCode学习总结文档；本文主要讲解贪心算法。💕💕😊

---

介绍

贪心算法是一种经典的算法策略，广泛应用于解决最优化问题。在许多情况下，贪心算法能够以简单且高效的方式解决复杂问题。因此，掌握贪心算法对开发人员和算法爱好者来说非常重要。本文旨在帮助读者深入理解贪心算法的工作原理、特征、正确性证明及其实际应用，并通过多个实例的分析和Python代码实现来巩固理解。

目标读者

本文适合有一定编程基础，尤其是具备基础算法和数据结构知识的读者，旨在帮助这些读者深入理解贪心算法并掌握其应用。

---

一、贪心算法基础

1. 什么是贪心算法？

贪心算法是一种在每一步选择中都采取当前状态下最优或最有利的选择，从而期望通过局部最优解最终得到全局最优解的算法。

• 定义：贪心算法是一种逐步构建解的算法，每一步都选择当前看起来最好的局部解决方案，并希望这些局部解决方案的集合能够产生全局最优解。
• 核心思想：局部最优 -> 全局最优。

2. 贪心算法的特征

贪心算法在使用时需要满足两个特征：

1. 贪心选择性质：即从局部最优的角度出发，当前的最优选择不依赖于未来的选择。每一步的选择是局部最优解。
2. 最优子结构：即问题的最优解由其子问题的最优解组成。这意味着问题可以通过递归的方式求解，且子问题的最优解与整个问题的最优解是一致的。

3. 贪心算法的优缺点

• 优点：简单、高效，通常时间复杂度较低。由于不需要像动态规划那样保存子问题的解，贪心算法的空间复杂度也较低。
• 缺点：贪心算法不能保证在所有问题上都能找到全局最优解，它只适用于能够满足贪心选择性质和最优子结构性质的问题。选择错误的策略，可能导致非最优解。

---

二、贪心算法的工作原理

1. 贪心算法的三步走

贪心算法可以通过以下三步来求解问题：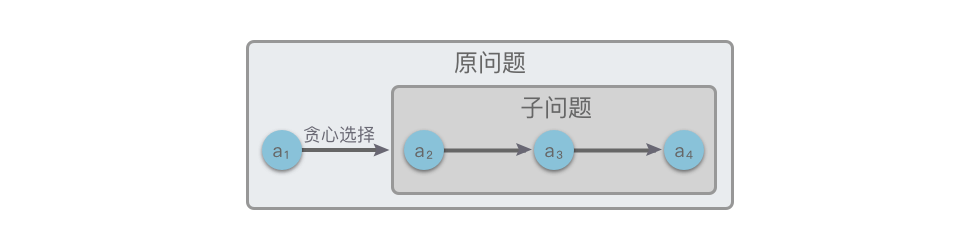

1. 转换问题：将复杂的问题转换为子问题，使得每一步都有一个明确的最优选择。
2. 贪心选择性质：在每一步中选择当前最优解，从而构建局部最优解。

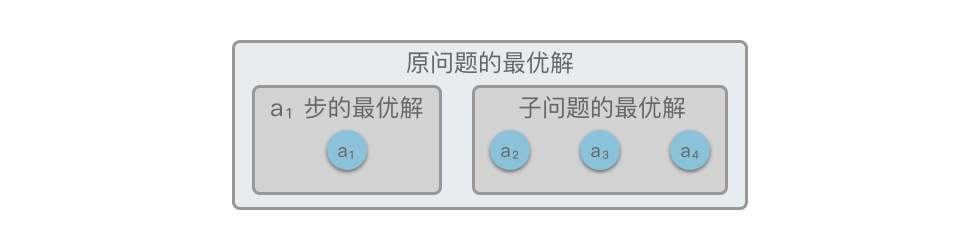
3. 最优子结构性质：将每一步的局部最优解结合起来，最终得到全局最优解。

如果不能利用子问题的最优解推导出整个问题的最优解，那么这种问题就不具有最优子结构。😎

2. 贪心算法的正确性证明

要证明贪心算法能够求解问题的最优解，常用以下两种方法：

1. 数学归纳法：先计算出边界情况（例如 n=1）的最优解，然后再证明对于每个 n，$F_{n+1}$ 都可以由 $F_n$ 推导出。
2. 交换论证法：从最优解出发，在保证全局最优不变的前提下，如果交换方案中任意两个元素 / 相邻的两个元素后，答案不会变得更好，则可以推定目前的解是最优解。

---

三、贪心算法的应用实例

接下来作者将通过几个经典问题来演示贪心算法的实际应用，并通过Python代码来解释每个问题的贪心策略。

1.分发饼干问题

问题描述：假设你有若干孩子和若干饼干，每个孩子有一个胃口值，每个饼干有一个尺寸。当且仅当某个饼干的尺寸大于等于某个孩子的胃口值时，该孩子才会得到饼干。你的目标是尽可能满足更多的孩子。

贪心策略：优先满足胃口最小的孩子，因为最小的胃口更容易得到满足。

代码实现：

def find_content_children(g, s):"""分发饼干问题:param g: 孩子的胃口数组:param s: 饼干的尺寸数组:return: 能满足的最大孩子数量"""# 对孩子的胃口和饼干尺寸进行排序g.sort()s.sort()child_i = 0cookie_i = 0# 遍历饼干和孩子，尽量满足更多的孩子while child_i < len(g) and cookie_i < len(s):if s[cookie_i] >= g[child_i]:# 如果当前饼干能满足当前孩子，分发饼干child_i += 1cookie_i += 1  # 无论是否满足孩子，尝试下一个饼干return child_i# 示例
g = [1, 2, 3]
s = [1, 1]
print(find_content_children(g, s))  # 输出: 1

过程分析：

1. 首先将孩子的胃口数组 g 和饼干尺寸数组 s 排序。
2. 通过遍历饼干和孩子，尽量让每个饼干满足胃口最小的孩子。
3. 使用贪心策略，尽可能满足最多的孩子。

2. 无重叠区间问题

问题描述：给定一组区间，找到最少移除的区间数量，使得剩余区间互不重叠。

贪心策略：按结束时间排序，优先选择结束时间最早的区间。

代码实现：

def erase_overlap_intervals(intervals):"""无重叠区间问题:param intervals: 区间数组:return: 需要移除的最小区间数量"""if not intervals:return 0# 按区间的结束时间进行排序intervals.sort(key=lambda x: x[1])end = intervals[0][1]count = 0# 遍历所有区间for i in range(1, len(intervals)):if intervals[i][0] < end:# 如果当前区间与前一个区间重叠，则移除count += 1else:# 否则，更新结束时间end = intervals[i][1]return count# 示例
intervals = [[1, 2], [2, 3], [3, 4], [1, 3]]
print(erase_overlap_intervals(intervals))  # 输出: 1

过程分析：

1. 将区间按照结束时间排序，结束时间越早，后续可选择的空间越大。
2. 遍历区间，检查当前区间是否与前一个区间重叠，如果重叠则移除当前区间。

3. 柠檬水找零问题

问题描述：你正在卖柠檬水，每位顾客给你 5、10 或 20 美元，你需要找零。假设一开始你没有任何零钱，问你能否在所有顾客完成交易后成功找零。

贪心策略：优先使用大面额的钞票找零。

代码实现：

def lemonade_change(bills):"""柠檬水找零问题:param bills: 顾客支付的钞票数组:return: 是否能够找零成功"""five = ten = 0for bill in bills:if bill == 5:five += 1elif bill == 10:if five == 0:return Falsefive -= 1ten += 1else:if ten > 0 and five > 0:ten -= 1five -= 1elif five >= 3:five -= 3else:return Falsereturn True# 示例
bills = [5, 5, 5, 10, 20]
print(lemonade_change(bills))  # 输出: True

过程分析：

1. 当顾客支付 10 美元时，优先找 5 美元。
2. 当顾客支付 20 美元时，优先找 10 美元和 5 美元，如果没有 10 美元，则找 3 张 5 美元。
3. 如果无法找零，返回 False。

4. 分发糖果问题

问题描述：给定 N 个孩子，每个孩子有一个评分。你需要按照评分的高低给每个孩子发放糖果，保证评分高的孩子获得更多糖果，要求使用最少的糖果。

贪心策略：

两次遍历，分别从左到右和从右到左，确保每个孩子都得到符合规则的糖果。

代码实现：

def candy(ratings):"""分发糖果问题:param ratings: 孩子的评分数组:return: 最少的糖果数量"""n = len(ratings)candies = [1] * n# 从左到右遍历for i in range(1, n):if ratings[i] > ratings[i - 1]:candies[i] = candies[i - 1] + 1# 从右到左遍历for i in range(n - 2, -1, -1):if ratings[i] > ratings[i + 1]:candies[i] = max(candies[i], candies[i + 1] + 1)return sum(candies)# 示例
ratings = [1, 0, 2]
print(candy(ratings))  # 输出: 5

过程分析：

1. 从左到右遍历，确保评分高的孩子获得比左边多的糖果。
2. 从右到左遍历，确保评分高的孩子获得比右边多的糖果。
3. 两次遍历后，每个孩子的糖果数量即为最终结果。

---

四、贪心算法的局限性与扩展

1. 局限性

贪心算法并不总能保证全局最优解。对于某些问题，贪心策略可能导致次优解。下面是一个经典的反例：

• 反例：最小化硬币找零问题
  在找零问题中，如果贪心地选择面额最大的钱币，可能无法找到最优解。例如，当找零为 14 时，面额为 10、7 和 1 的硬币，贪心算法会选择 10 和 4 个 1 元硬币，而最优解应为两个 7 元硬币。

2. 扩展

• 动态规划与贪心算法的对比：动态规划通过保存子问题的最优解，能够处理更多复杂的最优化问题，适用于贪心算法不适合的场景。
• 启发式算法：在某些复杂问题中，启发式算法可以作为贪心算法的扩展，用于近似求解复杂问题。

---

五、总结

总而言之，贪心算法是一种简单、高效的算法，适用于某些具有贪心选择性质和最优子结构性质的问题。通过几个经典问题的学习和实践，读者可以掌握贪心算法的应用。读者也可以深入学习动态规划、启发式算法等更高级的算法，进一步提升算法能力。😎👌

---

相关链接

• 项目地址：LeetCode-CookBook
• 相关文档：专栏地址
• 作者主页：GISer Liu-CSDN博客

如果觉得我的文章对您有帮助，三连+关注便是对我创作的最大鼓励！或者一个star🌟也可以😂.