
摘要节选:
反常能思特效应(ANE)产生垂直于温度梯度的横向电压。与用于能量转换的纵向热电相比,它具有电子和热输运解耦、更高的灵活性和更简单的横向结构等优点。
在这项工作中,从理论上证明了一对Dirac节点在Zeeman场下表现出奇数分布,双峰异常霍尔电导率曲线,其化学势和补偿载流子特征,导致与具有两个Weyl节点的简单Weyl半金属相比,ANC增强。
引言节选:
ANE的驱动力可分为外在贡献和内在贡献。外在贡献是指磁振子的阻力或强自旋-轨道耦合引起的斜散射和侧跃,而内在贡献则归因于能带的Berry曲率的影响。
Berry曲率表现为磁场在动量空间中使电子偏转,在带交叉点如Weyl点或节点线处发散。因此,相应的拓扑半金属有利于表现出较大的反常霍尔电导率(AHC) 。
Mott关系反映了AHC-σ和ANC-α之间的联系,它们都与Berry曲率通过布里渊区的积分有关。在低温极限下,莫特关系表示为:
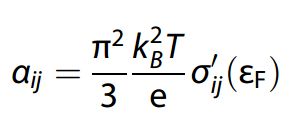
Mott关系表明,ANC-α的最大值出现在AHC-σ斜率最陡的能量处。因此,在费米能级εF的一侧具有相反AHC峰的能带结构有望承载较大的ANC。
从Zeeman场下Dirac半金属的模型哈密顿量出发,揭示了两对Weyl点在动量空间中形成““G-type””手性构型,从而导致AHC的双峰特征,化学势的奇数分布。这样的系统还具有补偿的载流子浓度,使两种类型的载流子都经历了相同符号的贝里曲率。
理论模型
Zeeman场下Dirac半金属的双峰AHC
Weyl点是动量空间中Berry曲率发散的带交叉位置,称为Berry曲率的源或汇(source or sink)。
首先,一个两带Weyl模型系统的最小哈密顿量可以写成:
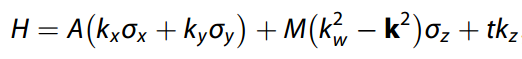
A和M分别与费米速度和带边附近有效质量的倒数有关。这样一个三维最小模型描述了一对位于(0;0;±kw),能量差2tkw的Weyl节点。
下图a显示了倾斜的两带Weyl模型的能带结构。反常霍尔电导率是化学势的偶函数(下图b),在Ef=0 eV处有一个峰值。而相应的由莫特关系推导出的ANC曲线是关于化学势的奇函数。ANC的两个相对峰与AHC曲线的最大斜率相连接,对称地位于费米能级的上下,(下图c)。
Zeeman场下Weyl模型和Dirac模型的电子结构和输运性质。
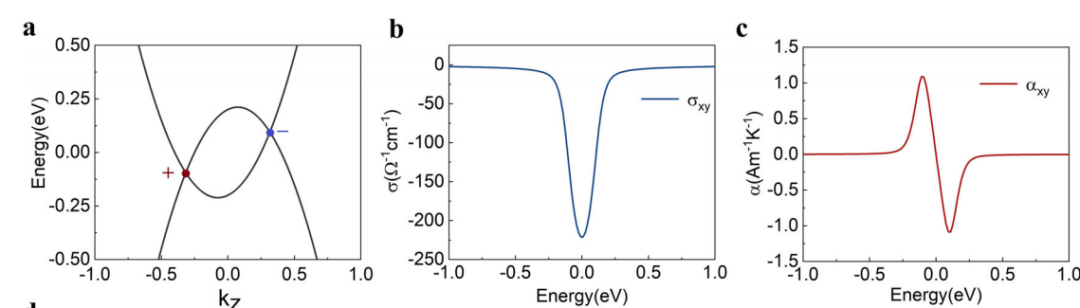
总之,一对手性相反的Weyl点在费米能级上只产生一个AHC峰。这样的单峰Weyl模型会在远离费米能级的地方产生中等的ANE,而费米能级处的ANE正好为零。
为了在费米能级上获得增强的ANC值,需要AHC曲线是一个奇函数,在狭窄的能量区间内,两个相反的峰位于费米能级的上方和下方。这需要至少四个Weyl节点,其中一对位于费米能级以下,另一对位于费米能级以上,形成手性的“G-type”排列。
这里采用采用Dirac模型,即两带Weyl模型与其时间反转相连接,并结合打破时间反转对称性的Zeeman项,式中S为Zeeman项强度。
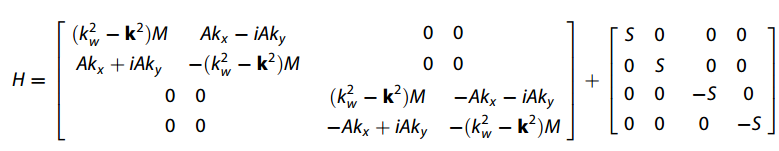
哈密顿量简洁的形式:
![]()
没有Zeeman项,能带是双简并的,有两个Dirac点由两个手性相反的简并Weyl节点组成。由于时间反演对称性,AHC和ANC都消失。
相反自旋通道的Weyl点使得时间反演对称性破坏,AHC和ANC则显现并得到增强。
相同参数下,令Zeeman项S=0.05 eV,手性倾斜Weyl模型出现了四个Weyl点,如下图d所示,在费米能级周围形成“G-type”构型。AHC相对于化学势呈奇数分布(下图e),两个相对的峰对称地位于费米能级的上方和下方。相应的ANC曲线对化学势呈偶函数,符合莫特关系。
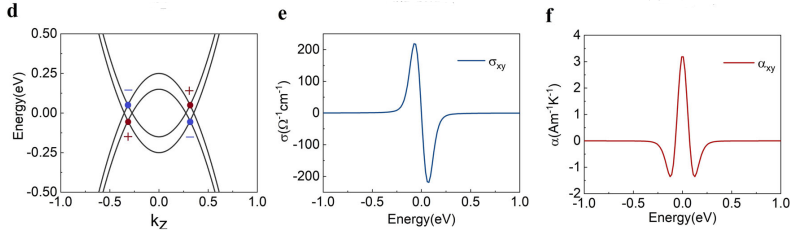
在单峰Weyl模型中,ANC曲线在费米能级为零处接近零,而在双峰Dirac模型中,ANC曲线恰好在费米能级处显示出最大值,几乎是Weyl模型最大值的300%。
因此,具有Zeeman项的四带Dirac模型显示了两个AHC峰,并在费米能级上增强了ANC,为设计ANC材料提供了一个典型的能带特性。
哈密顿量中a、M、kw和S分别与费米速度、带边有效质量的倒数、动量空间中两个Dirac节点的距离和Zeeman场的强度有关。在实际材料中,这些物理参数可以通过应变、元素替代、磁邻近效应和外磁场等来调节。
下图显示了在不同温度下,在Ef0处的最大ANC峰(上图f)相对于这四个物理参数的变化。
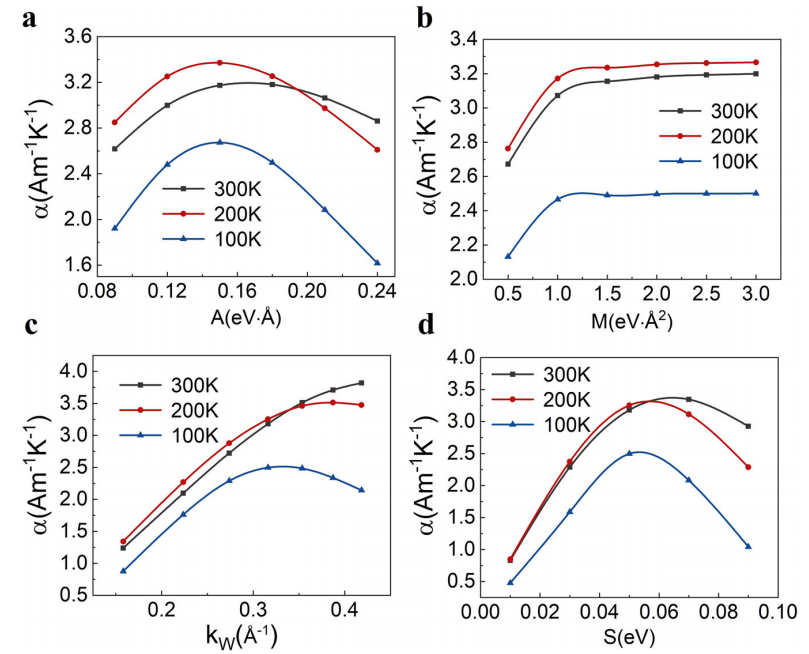
ANC的峰值随费米速度A先增大后减小,费米速度A描述了狄拉克点周围能带的斜率。ANC最大值呈有效质量M的反比增大趋势,即随着有效质量在带边缘附近的增大而减小。带边缘附近的有效质量越小,Dirac点周围的带就越陡峭,同时AHC的峰值也越大,从而导致ANC越大。
随着两个Dirac点距离kw的增加,ANC的峰值逐渐增大。Zeeman场的强度与两个自旋通道的能量分裂和AHC相对峰的能量间隔有关。Zeeman场强S越大,时间反转对称性的破坏越强,ANC越大,AHC两峰能量间隔越大,AHC斜率越小,ANC受到抑制。
这种竞争机制使得ANC的最大值先增大后减小。
计算模型
Na3Bi
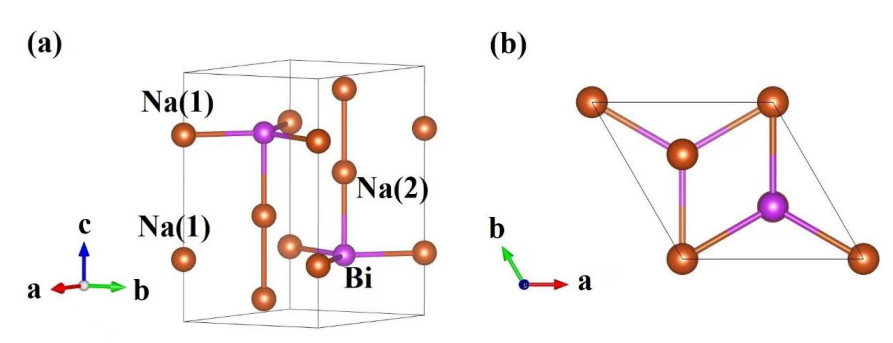
space group 𝑃63/𝑚𝑚𝑐 ( No. 194)
𝑎 = 𝑏 =5.459Å 𝑐 = 9.675Å
Na 1:2b position( 0.0, 0.0, 0.25)
Na 2:4f position(0.333, 0.667, 0.583)
Bi :2c position (0.333, 0.667,0.25)
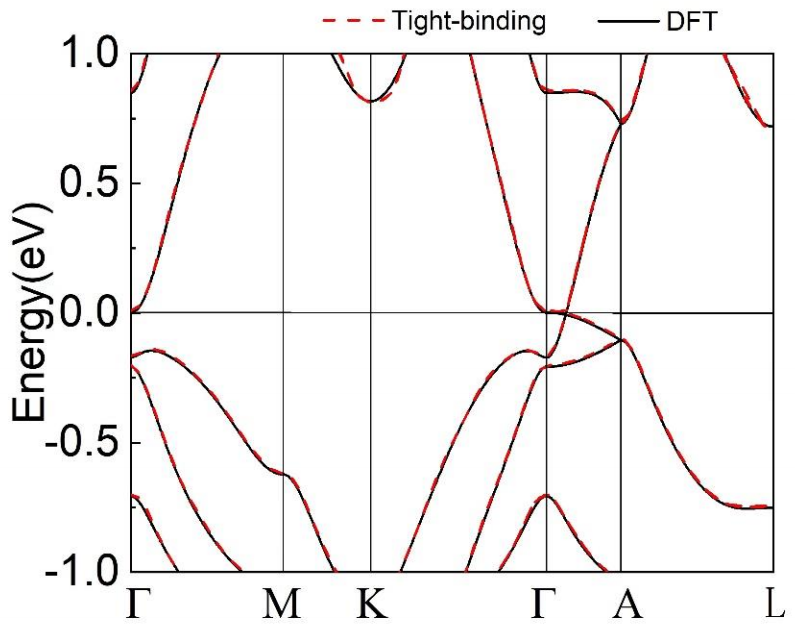
由DFT和Tight-binding得到的Na3Bi的能带结构。Dirac点是受C3旋转对称保护的偶然简并。
哈密顿量构造
Na3Bi采用费米能级附近的Na-3s和Bi-6p态,构建了一个具有万尼尔轨道的TB模型 HTB,并添加了如下所示的Zeeman项:
![]()
Zeeman场下Na3Bi的电子结构和输运性质如下图。
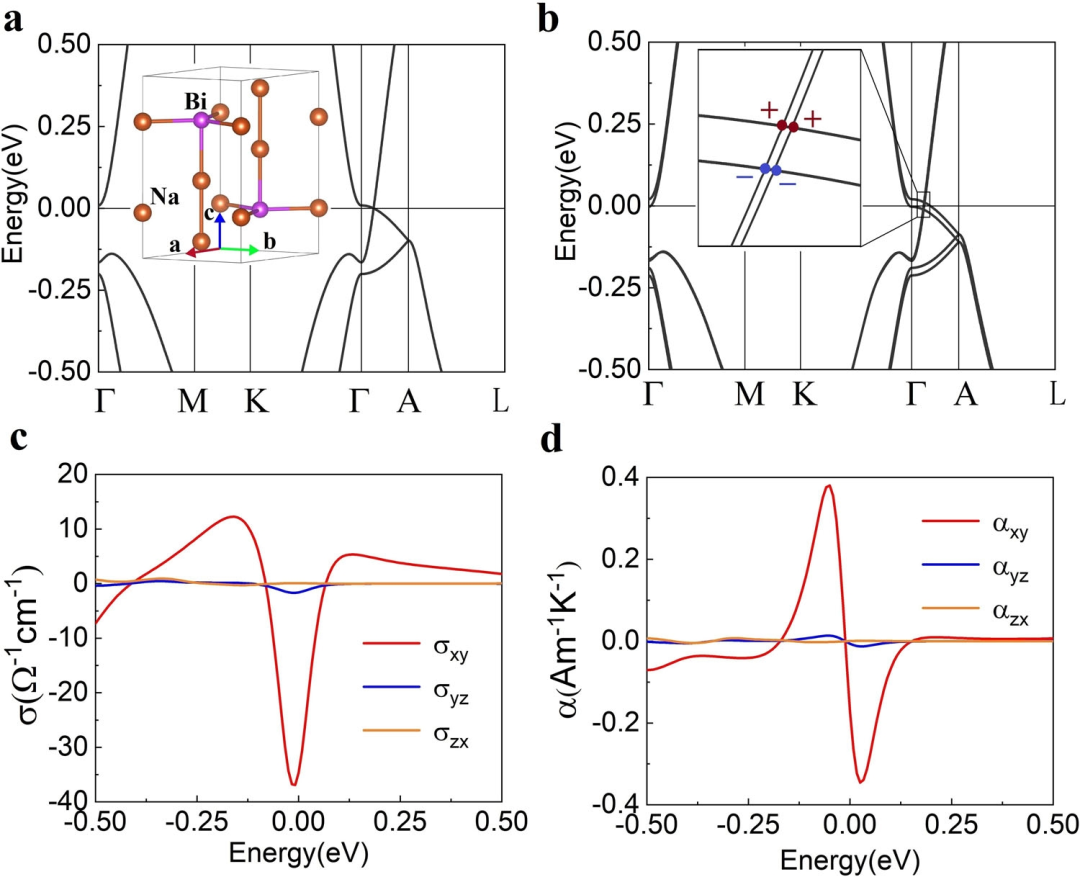
上图b为23meV Zeeman电场下Na3Bi的能带结构以及在Zeeman场下Na3Bi的 AHC和 ANC与化学势的关系。由这里的Zeeman场只沿z轴,AHC和ANC的yz和zx分量与xy分量相比几乎可以忽略不计。
由于Na3Bi Dirac点的较陡分支在Zeeman场下几乎不会分裂,因此不会出现双峰AHC的特征。
NaTeAu
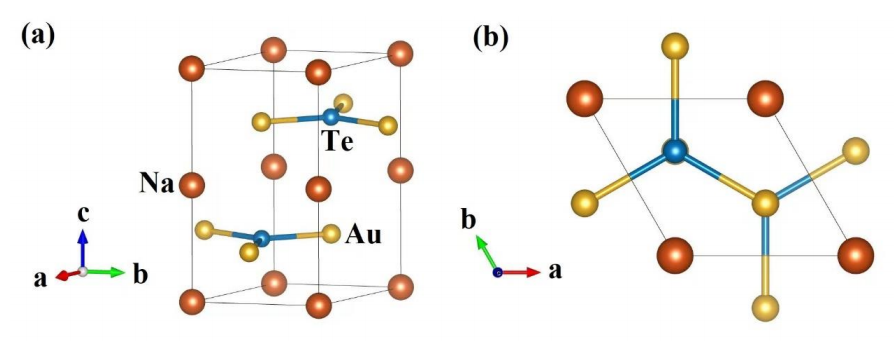
space group 𝑃63/𝑚𝑚𝑐 (No. 194)
𝑎 = 𝑏 =4.710Å and 𝑐 = 8.688Å
Na 2a position (0.0, 0.0, 0.0)
Te 2c position (0.333, 0.667, 0.25)
Au 2d position (0.333, 0.667, 0.75)
NaTeAu的能带结构
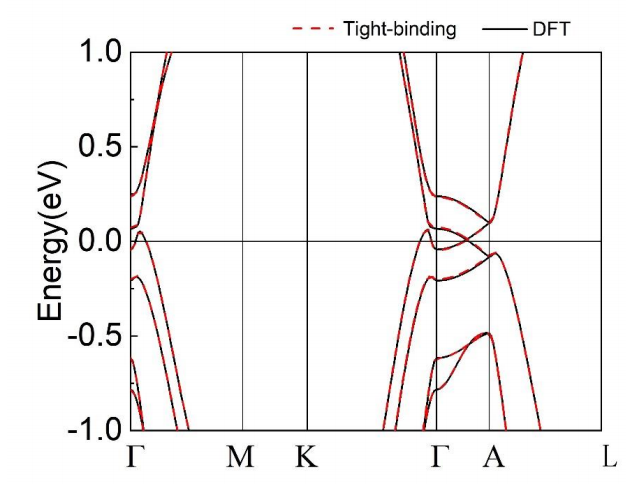
NaTeAu中Te和Au原子分别位于A和B位上构建蜂窝晶格;Na原子形成三角形晶格,沿c方向与蜂窝晶格交替堆叠。NaTeAu的Dirac节点位于Γ — A线上,受到C3旋转对称的保护。
通过采用费米能附近的Na-3s Te-5s, 5p和Au-5d, 6s态,构建了具有Zeeman项的NaTeAu的有效哈密顿量。
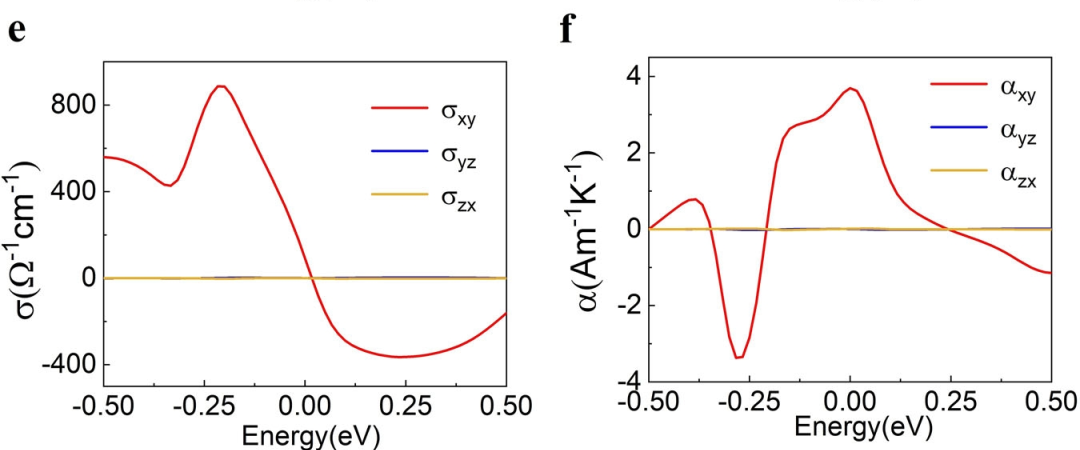
Zeeman场下NaTeAu的电子结构和输运性质。
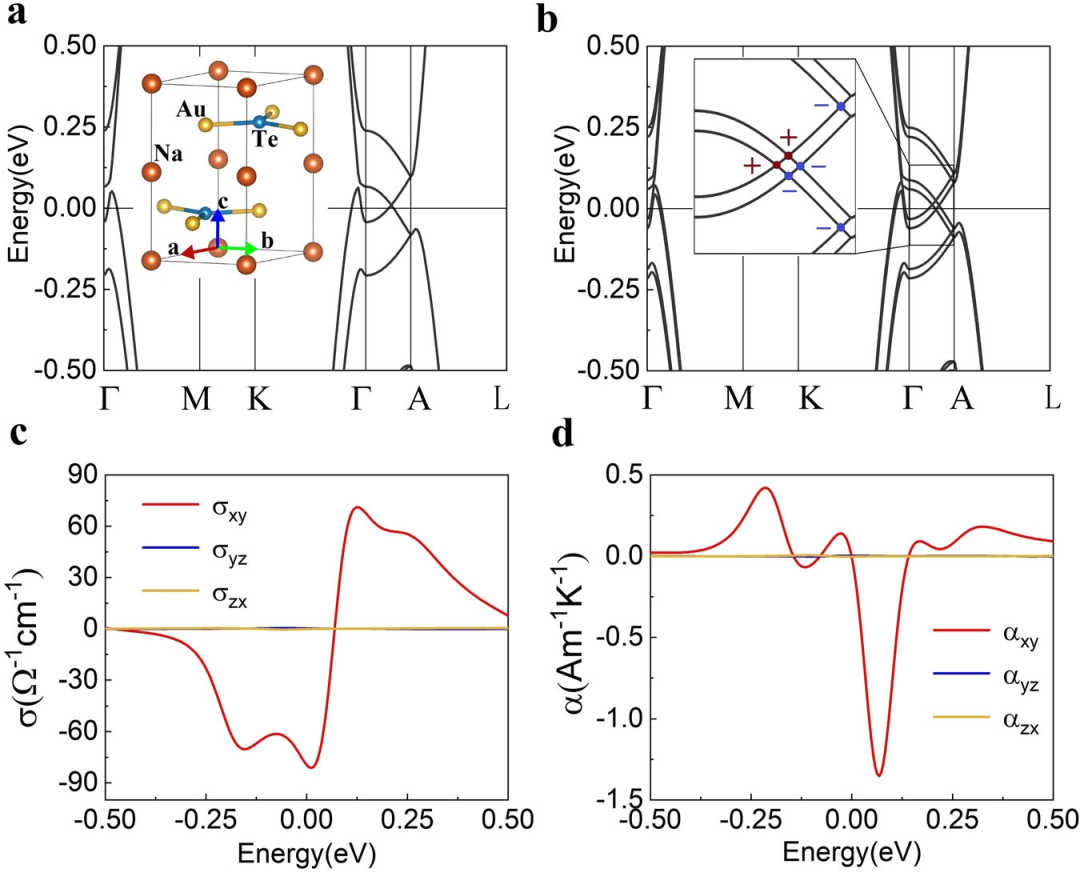
由于自旋分裂的Dirac能带结构,NaTeAu的AHC (σxy)在E = 0.01 eV和E = 0.13 eV处出现两个符号相反的峰。因此,αxy的ANC曲线在E = 0.07 eV处呈现一个峰,符合四段Dirac模型的特征。
在Na3Bi和NaTeAu中,横向能斯特电导率是由贝里曲率效应驱动的,其中外部磁场的存在是为了诱导塞曼分裂。
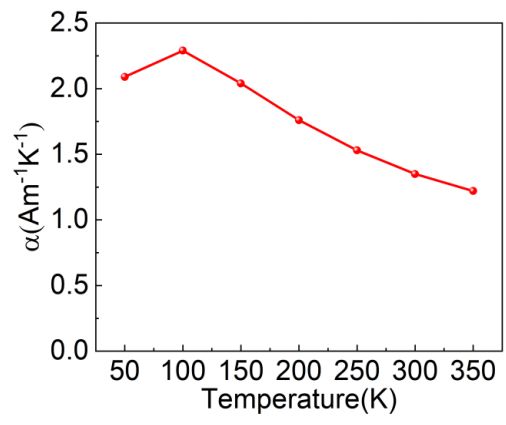
NaTeAu相对于温度的最大ANC。
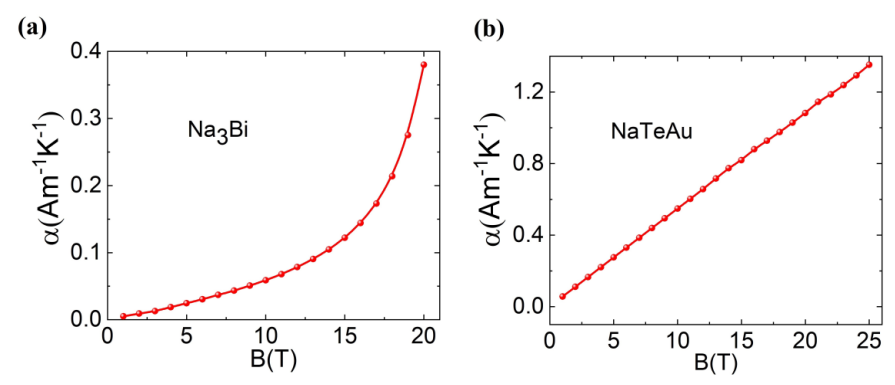
Na3Bi和NaTeAu的最大反常能斯特电导率(ANCs)与磁场的关系。在较小的磁场下, ANCs变为非零。
磁场强度的估算

NaFeTe2Au2
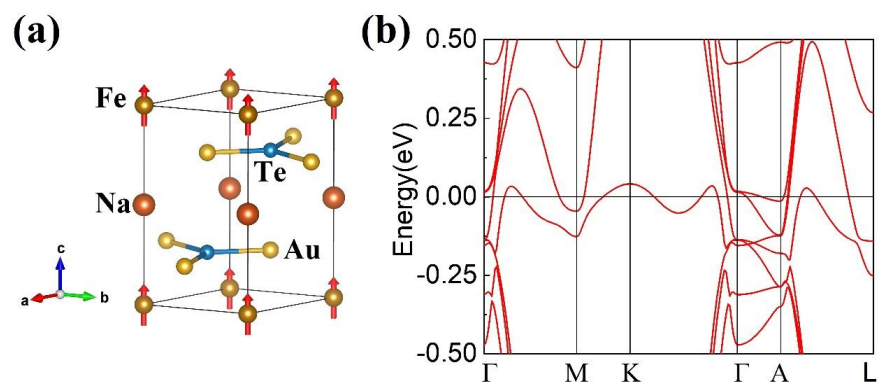
space group P-3m1 (No. 164)
a = 4.710 Å and c = 8.688 Å.
Na, Fe, Te, and Au atoms occupying the Wyckoff positions 1a, 1b, 2d, and 2d。
通过用Fe取代NaTeAu中50%的Na,设计了一种本征磁性拓扑材料NaFeTe2Au2。Fe离子形成铁磁性结构,提供本征Zeeman分裂。
Co2PdGe
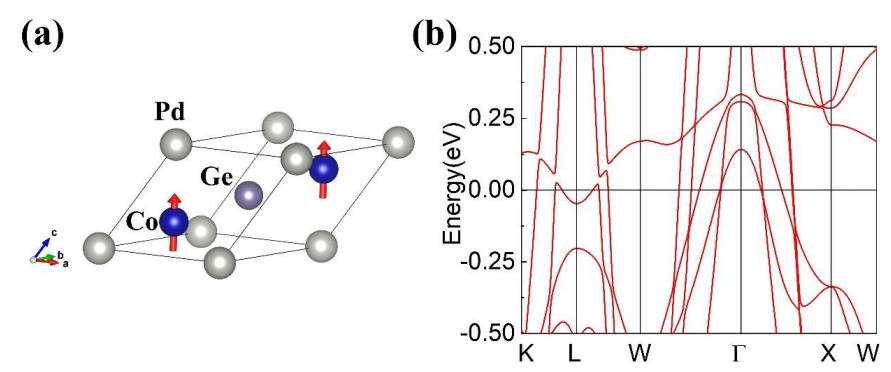
space group Fm-3m (No. 225)
a=b=c= 4.386 Å.
Co, Pd and Ge atoms occupy the 8c, 4a, and 4b Wyckoff positions
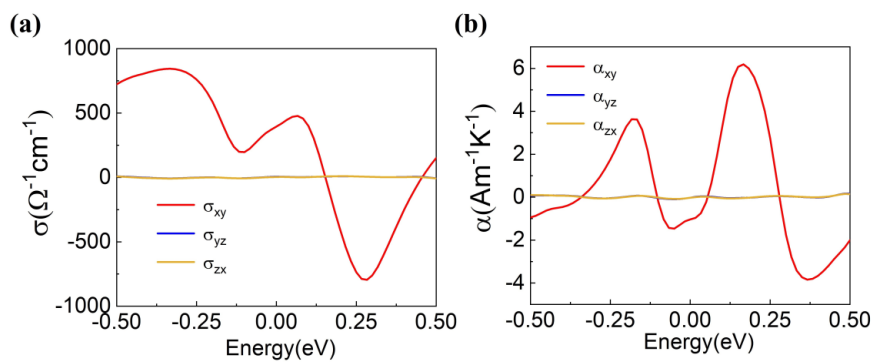
Heusler材料Co2PdGe的AHC和 ANC
计算方法
基本理论
反常霍尔电导率(AHC) σ,用Kubo公式计算
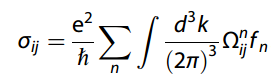
反常能斯特电导率(ANC)可以用类高斯函数w代替费米-狄拉克分布函数f得到
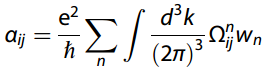
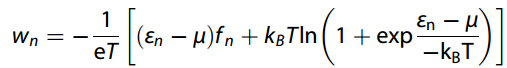
在低温下,简化为莫特关系式
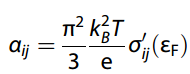
Berry曲率Ω由Kubo公式求得
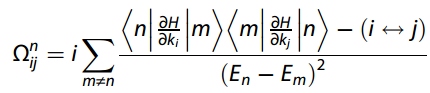
计算软件
Vienna ab initio simulation package (VASP),Wannier90,WannierTools。
