插入排序与希尔排序

前言

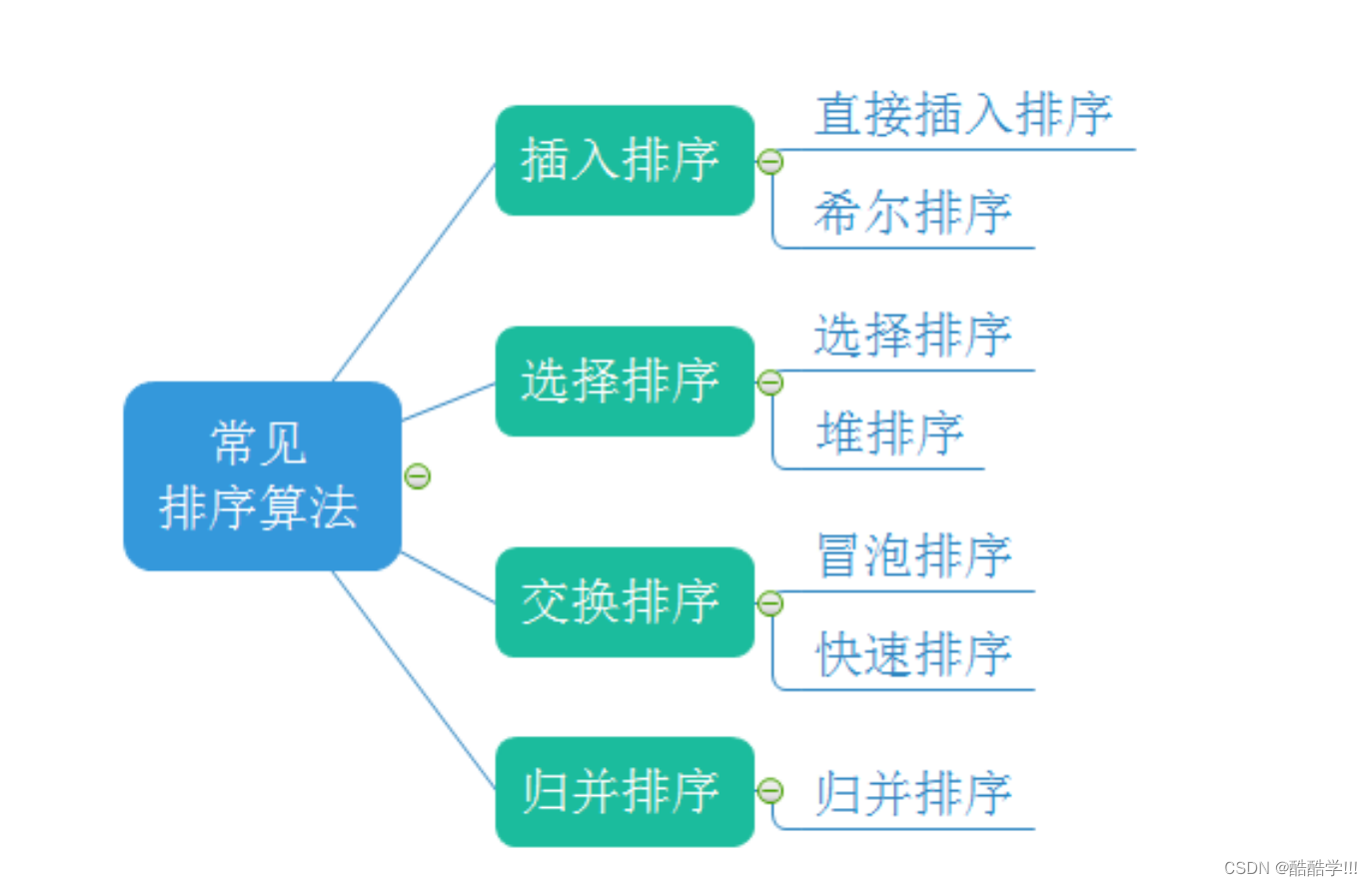
如图所示为常见的排序算法, 前面我们已经了解了堆排序和冒泡排序, 本篇旨在介绍插入排序以及插入排序的优化版本希尔排序.

插入排序和希尔排序都是基于比较的排序算法，都属于插入类排序算法。插入排序是一种简单直观的排序算法，其基本思想是将待排序的元素逐个插入到已排序的序列中的合适位置。希尔排序是对插入排序的改进，通过将序列分割成若干子序列来进行排序，最终达到整个序列有序的目的。

博客主页: 酷酷学!!!

感谢关注~

插入排序

如上图所示,
当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移

直接插入排序的特性总结：

1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定

代码如下:

//插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}

直接插入排序思想:

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。
实际中我们玩扑克牌时，就用了插入排序的思想

代码解释: 首先先看单趟排序, 当end=0时, 即前一个数据可以看作是有序的, 然后我们拿后面的数据与排序好的数据进行比较, 如果是升序, 则小于前面的数据的话, 就将前一个位置往后移动, 这里我们创建了临时变量来保存a[end+1]的值, 如果遇到大于的数字就停下来, 然后进行插入, 这里我们先跳出循环然后再插入, 因为如果当最后一次为0位置时进入循环, tmp<a[end]条件还成立 , 但是下一次就进入不了循环了, 所以我们跳出循环然后插入元素.

希尔排序

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达 gap=1 时，所有记录在统一组内排好序。

希尔排序分为两个步骤:

1. 预排序(让数组接近有序)
2. 插入排序

预排序, 首先把数据分为gap个组, 如下图所示, 分为三个组, 间隔为三的是一组的数据, 然后分别可以对每组的数据进行排序.

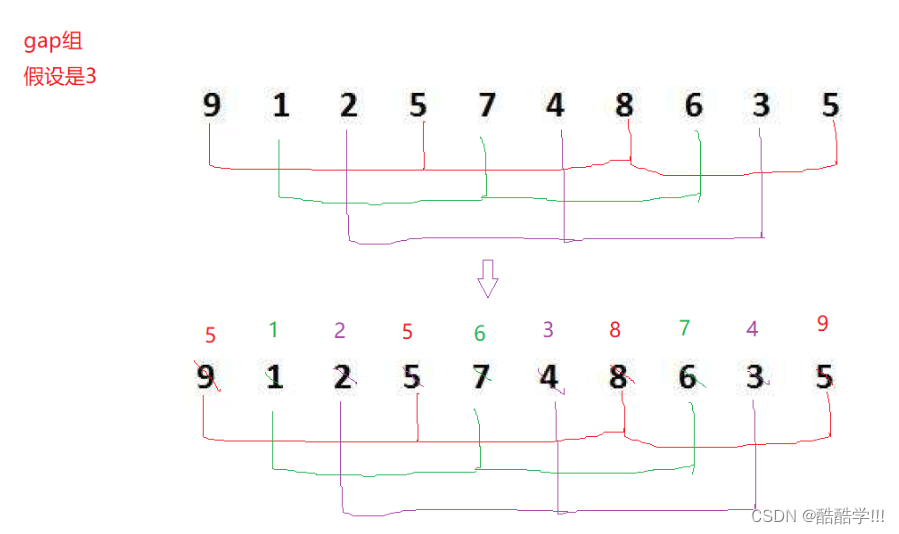
以红色的组为例, 对这组数据进行排序

代码如下:

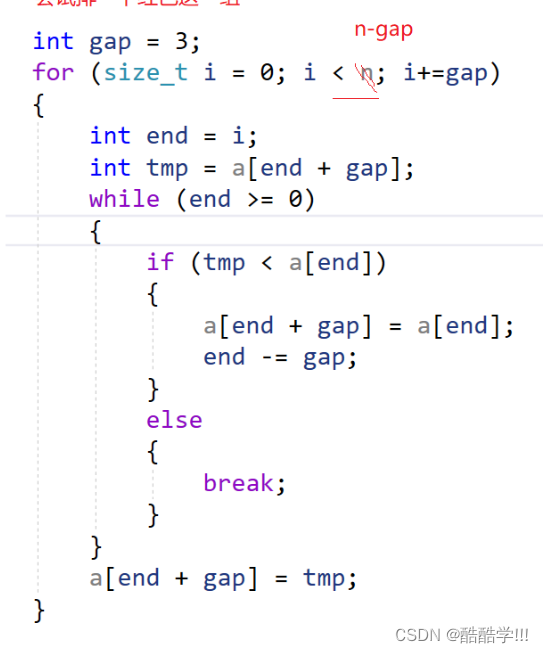
这里的结束条件为n-gap, 因为红色那组数据最后一个数据也就是5,当访问到8时最后一个数据就可以进行排序, 如果条件为n的话会造成越界, 绿色那组和紫色那组也是一样, n-gap前都可以访问到.

然后我们把每组都进行预排序, 可以分开写, 也可以合并写.

一组一组的排序

多组并走:

预排序的目的是为了让数据接近有序, 而不是真正的有序, 比如一个很大数,如果不能进行预排序, 就需要一次一次移动, 但是如果预排序的话就可以一次移动gap个位置, 这样效率会有所提升.

那什么是希尔排序呢, 希尔排序就是进行多组预排序, 当gap==1时就是插入排序, 我们就可以先进行预排序, 然后进行插入排序.

代码如下:

void ShellSort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end+gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

这里gap每次缩小三倍是比较高效的, +1是为了防止gap==0的情况没法进行最后一次的插入排序.

以下是对gap=gap/3+1的解释说明:

《数据结构-用面相对象方法与C++描述》— 殷人昆

希尔排序的特性总结：

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就
   会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的
   希尔排序的时间复杂度都不固定：

那么我们也可以简单分析一下它大概的时间复杂度

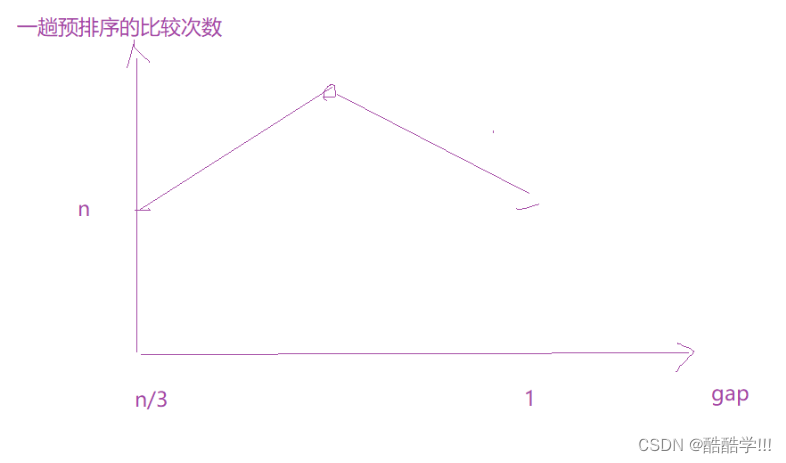
gap组数据, 假设忽略掉+1(方便计算) , 每组数据个数 = n/gap

1. gap = n/3 , 每组3个数据, 最坏情况下, 第一趟的排序消耗, 每组比较的次数 * 组数 , 即(1+2) * n/3, 即n
2. gap = n/9 , 每组9个数据, 最坏情况下, 第二趟排序的消耗(1+2+3+…+8)*n/9 即4n

…

3. 最后一趟已经很接近有序了, gap==1 , 就是直接插入排序, 销毁为n

大概的消耗如图所示, 我们也可以简单记忆希尔排序的时间复杂度大概是O(N^1.3)左右.

效率测试

下面代码使用了随机数生成, 生成十万个随机数, 然后进行测试, 使用clock()函数算出程序执行的时间

// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand() + i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();//SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();//QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();//MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{//int arr[] = { 23,4,5,64,776,34,2,3 };//PrintArr(arr, sizeof(arr) / sizeof(int));//BubbleSort(arr, sizeof(arr) / sizeof(int));//PrintArr(arr, sizeof(arr) / sizeof(int));TestOP();return 0;
}

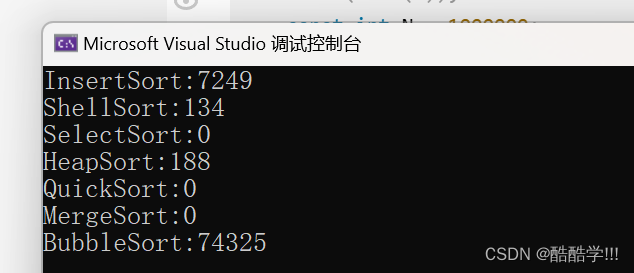
执行结果如下, 可以看到冒泡排序的执行时间最长, 插入排序的时间复杂度虽然也是O(N^2) , 但是效率比冒泡排序快很多, 而希尔排序和堆排序差不多是一个量级的.

全部代码

#define _CRT_SECURE_NO_WARNINGS 1
#include"Sort.h"void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void PrintArr(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}//插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}//希尔排序void ShellSort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end+gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}//冒泡排序
void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){//单趟int flag = 0;for (int i = 1; i < n-j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);flag = 1;}}if (flag == 0){break;}}}void Adjustdown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] < a[child + 1]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//堆排序
void HeapSort(int* a, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){Adjustdown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);Adjustdown(a, end, 0);--end;}
}

总结

插入排序和希尔排序都是比较简单的排序算法，适用于小规模数据的排序。插入排序是一种直观的算法，希尔排序是插入排序的改进算法，通过分组和逐步缩小增量的方式提高了排序的效率。

您的支持是我最大的动力, 感谢~