样本均值与样本方差的定义
首先来看一下均值,方差,样本均值与样本方差的定义
总体均值的定义:
μ = 1 n ∑ i = 1 n X i \mu=\frac{1}{n}\sum_{i=1}^{n} X_i μ=n1i=1∑nXi
也就是将总体中所有的样本值加总除以个数,也可以叫做总体的数学期望或简称期望
总体方差的定义:
σ 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 \sigma ^2=\frac {1}{n}\sum_{i=1}^{n} (X_i-\mu)^2 σ2=n1i=1∑n(Xi−μ)2
总体中全部样本各数值与总体均值差的平方和的平均数,用来衡量随机变量或一组数据离散程度的度量。
在实际应用中,我们一般是拿不到总体的均值与总体的方差,只能通过抽样得到的样本均值与样本方差来估计总体的均值与方差。于是我们就得到了样本均值和样本方差:
样本均值的定义
X ˉ = 1 n ∑ i = 1 n X i \bar {X}=\frac{1}{n}\sum_{i=1}^{n} X_i Xˉ=n1i=1∑nXi
样本方差的定义
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S^2=\frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar X)^2 S2=n−11i=1∑n(Xi−Xˉ)2
对比总体方差的公式,样本方差的公式的系数为什么变为了 1 n − 1 \frac{1}{n-1} n−11?
通俗理解-自由度
一个比较通俗的的理解就是自由度,可以理解为对应的独立信息量。样本均值和样本方差就是抽样后把所有的独立的信息量(这里的独立的信息量就是数值,包含了均值和方差的信息)平均得到,在计算样本方差时用 X ˉ \bar X Xˉ替代了总体均值 μ \mu μ,自由度减少了一个。
假设只采样了两个样本 X 1 , X 2 X_1,X_2 X1,X2,这其中的信息量是多少呢?方差是计算样本之间的偏离程度,所以一个独立有效的信息量就是这个数值减去均值。在计算方差时分子有两项: ( X 1 − X ˉ ) 2 (X_1-\bar X)^2 (X1−Xˉ)2 和 ( X 2 − X ˉ ) 2 (X_2-\bar X)^2 (X2−Xˉ)2 . 要算第一个样本的偏离程度,毋庸置疑只能老老实实算 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ);但是,第二个样本呢?计算 ( X 2 − X ˉ ) (X_2-\bar X) (X2−Xˉ) 吗?其实还有另外一种方法,因为 X ˉ = X 1 + X 2 2 \bar X=\frac{X_1+X_2}{2} Xˉ=2X1+X2, X 1 X_1 X1 和 X 2 X_2 X2 其实是对于 X ˉ \bar X Xˉ对称的。所以其实 ( X 2 − X ˉ ) = ( 2 X ˉ − X 1 − X ˉ ) = − ( X 1 − X ˉ ) (X_2-\bar X)=(2\bar X-X_1-\bar X)=-(X_1-\bar X) (X2−Xˉ)=(2Xˉ−X1−Xˉ)=−(X1−Xˉ)。也就是我们在用样本均值 X ˉ \bar X Xˉ替代总体均值后,只要 X 1 X_1 X1确定了之后, X 2 X_2 X2是可以根据 X 1 X_1 X1推出来具体数值的,实际能够有效提供样本到 X ˉ \bar X Xˉ的偏移量的信息数只有一条 X 1 X_1 X1。
我们对这种现象可以有一个表述:就是 ( X 2 − X ˉ ) (X_2-\bar X) (X2−Xˉ) 是不自由的,因为从之前的式子可以推出它。当然,对称地,我们也可以说 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ)是不自由的。总之,这两个式子当中,只有一个是自由的,所以我们称这两个式子的自由度为 1.所以在两个样本求方差的时候要除1,应为实际应用到方差计算种的只有 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ)这一个有效信息。
同样,将样本数增加至三个,当有两个样本 X 1 , X 2 X_1,X_2 X1,X2并且知道 X ˉ \bar X Xˉ的情况下,我们就可以推出第三个样本 X 3 X_3 X3的值,对应的自由度为 2.
以此类推,当我们有 n n n个样本的时候,其自由度为 n − 1 n - 1 n−1.也就是说,当我们有 n n n 个样本的时候,我们虽然看起来在分子上做了 n n n 个减法,但实际上我们只算出了 n − 1 n - 1 n−1 个偏差量。因此,做平均的时候,要除以的分母就是 n − 1 n - 1 n−1
但是,为什么 n 个减法做完,自由度只有 n - 1?是谁从中搞鬼,偷走了一个自由度?答案很简单,是 X ˉ \bar X Xˉ 。注意在总体方差中,隐含的分布均值是 μ \mu μ ,这个均值是知道了总体的分布后计算出来的,而在样本方差中 μ \mu μ 是未知的,所以在估计方差之前,我们会需要先找一个 μ \mu μ 的代替,也就是 X ˉ \bar X Xˉ ,而 X ˉ \bar X Xˉ是根据样本算出来的. 也就是说,在用 X ˉ \bar X Xˉ 代替 μ \mu μ 的过程中,我们损失了一个自由度。
那么,如果问题的背景变了,我们知道隐含的分布均值 μ \mu μ ,只是不知道 σ 2 \sigma^2 σ2 ,那我们该如何估计 σ 2 \sigma^2 σ2?这种情况下求方差就变成了符合直觉的 ( X 1 − μ ) 2 + ( X 2 − μ ) 2 + ⋯ + ( X n − μ ) 2 n \frac{(X_1-\mu)^2+(X_2-\mu)^2+\dots+(X_n-\mu)^2}{n} n(X1−μ)2+(X2−μ)2+⋯+(Xn−μ)2。
严密推导过程
估计量的评选标准
当我们用抽样的方法去估计总体时,总是希望每次抽样的结果尽可能的靠近实际的总体评估量,同时抽取的样本越多时越接近实际的总体评估量。对于评估量的好坏有如下三个评价指标
无偏性
设 θ \theta θ是总体的未知参数, X 1 , X 2 , . . . . . X n X_1,X_2,.....X_n X1,X2,.....Xn是总体的一个样本, θ ^ \widehat \theta θ 是参数的一个估计量,若
E ( θ ^ ) = θ E(\widehat \theta)=\theta E(θ )=θ
则称 θ ^ \widehat \theta θ 是 θ \theta θ的一个无偏估计量
无偏性简单来说就是取样后得到的估计量 θ ^ \widehat \theta θ 的期望就等于总体的估计量。
考虑如下一个打靶的例子。如果有一个射击高手打靶,那么结果总会在靶心附近(总体期望 θ \theta θ),那么我们一般会通过打靶结果(也就是样本 θ ^ \widehat \theta θ )认为这是一个熟练的射击手,对于多次的打靶结果我们对其打靶结果的期望是靶心( E ( θ ^ ) = θ E(\widehat \theta)=\theta E(θ )=θ),也就是无偏的。
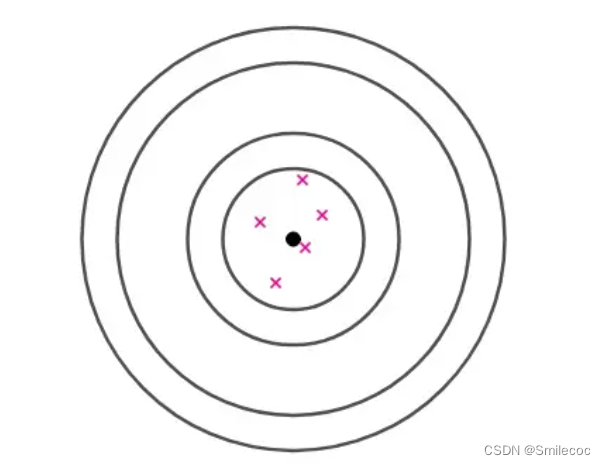
但如果出现了如下这种结果,通过这些样本我们就会猜测集中在一点附近可能是一个射击高手,这个偏差可能是由于瞄准镜歪了这种导致的呢
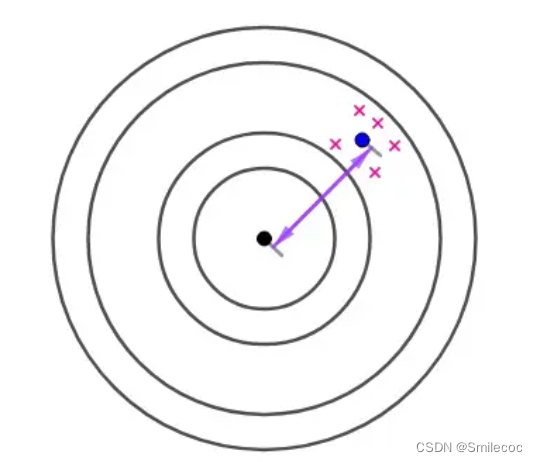
对于这种稳定影响结果的因素导致的偏差称为系统偏差,也就是 E ( θ ^ ) − θ E(\widehat \theta)-\theta E(θ )−θ。无偏估计的实际意义就是无系统偏差。很明显无偏估计更接近实际的总体统计量
有效性
若 θ ^ 1 {\widehat \theta}_1 θ 1和 θ ^ 2 {\widehat \theta}_2 θ 2都是样本 X 1 , X 2 , . . . . . X n X_1,X_2,.....X_n X1,X2,.....Xn的无偏估计量,若对于任意取值范围里有 D ( θ ^ 1 ) ≤ D ( θ ^ 2 ) D({\widehat \theta}_1) \le D({\widehat \theta}_2) D(θ 1)≤D(θ 2),
则 θ ^ 1 {\widehat \theta}_1 θ 1比 θ ^ 2 {\widehat \theta}_2 θ 2更加有效。
有效性就是同样无偏的估计量,更集中,方差更小的估计量更好
接着考虑如下打靶结果,虽然期望都是靶心,但是很明显后面的结果更加集中,相应的评估效果也会更好
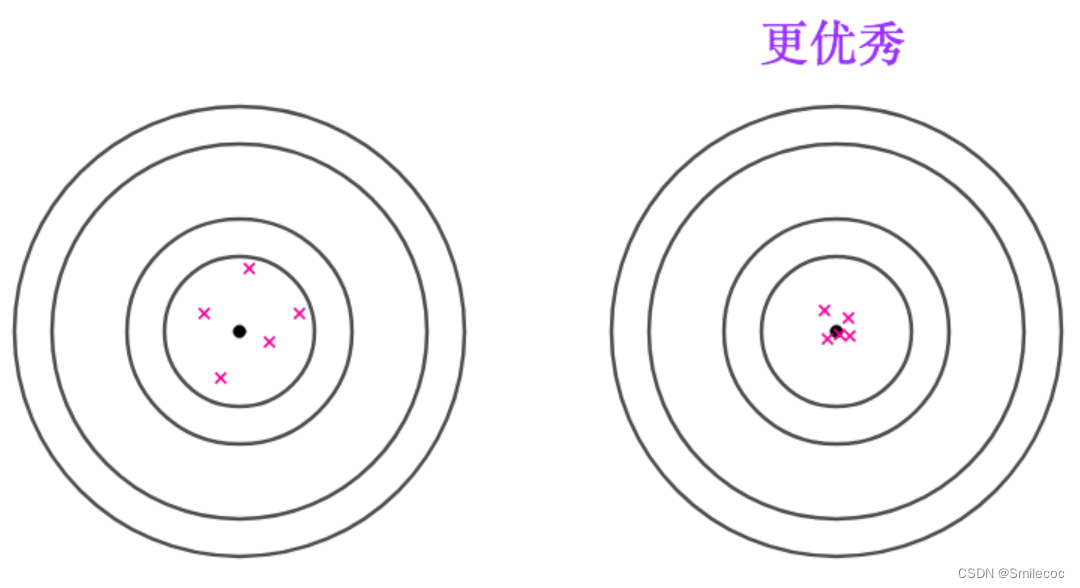
相合性
之前的无偏性和一致性都是在样本容量固定为n的情况下讨论的,而如果样本容量越来越多时,一个估计量能稳定于待估的参数真值
相合性大样本条件下,估计值等于实际值.对于任意 θ > 0 \theta >0 θ>0,有
lim n → ∞ P ( ∣ θ ^ − θ ∣ < ε ) = 1. \lim\limits_{n\to\infty}P\left(|\hat\theta-\theta| < \varepsilon\right)=1. n→∞limP(∣θ^−θ∣<ε)=1.
推导
首先来看一下在分母为n的情况下样本方差是不是总体方差的无偏估计量:
E ( S 2 ) = E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) − ( X ˉ − μ ) ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) 2 − 2 ( X i − μ ) ( X ˉ − μ ) + ( X ˉ − μ ) 2 ) ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + 1 n ( X ˉ − μ ) 2 ∑ i = 1 n 1 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] \begin{aligned} E(S^2) &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} \Bigg( (X_i - \mu)-(\bar X - \mu) \Bigg)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} \Bigg( (X_i - \mu)^2-2(X_i - \mu)(\bar X - \mu)+(\bar X - \mu)^2 \Bigg) \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ \frac{1}{n} (\bar X - \mu)^2 \sum_{i=1}^{n} 1 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ (\bar X - \mu)^2 \right ] \end{aligned} E(S2)=E[n1i=1∑n(Xi−Xˉ)2]=E n1i=1∑n((Xi−μ)−(Xˉ−μ))2 =E[n1i=1∑n((Xi−μ)2−2(Xi−μ)(Xˉ−μ)+(Xˉ−μ)2)]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+n1(Xˉ−μ)2i=1∑n1]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]
其中
X ˉ − μ = 1 n ∑ i = 1 n X i − 1 n ∑ i = 1 n μ = 1 n ∑ i = 1 n ( X i − μ ) \bar X - \mu=\frac{1}{n}\sum_{i=1}^{n} X_i-\frac{1}{n}\sum_{i=1}^{n} \mu=\frac{1}{n}\sum_{i=1}^{n} (X_i-\mu) Xˉ−μ=n1i=1∑nXi−n1i=1∑nμ=n1i=1∑n(Xi−μ)
接着计算有:
E ( S 2 ) = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ⋅ n ⋅ ( X ˉ − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] − E [ ( X ˉ − μ ) 2 ] = σ 2 − E [ ( X ˉ − μ ) 2 ] \begin{aligned} E(S^2) &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \cdot n \cdot (\bar X - \mu)+ (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2 \right ]- E \bigg [(\bar X - \mu)^2 \bigg ] \\ &= \sigma^2-E \bigg [(\bar X - \mu)^2 \bigg ] \end{aligned} E(S2)=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)⋅n⋅(Xˉ−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2]−E[(Xˉ−μ)2]=σ2−E[(Xˉ−μ)2]
可以看到同样在除以 n n n的情况下只有当 X ˉ = μ \bar X = \mu Xˉ=μ时才有 E ( S 2 ) = σ 2 E(S^2)= \sigma^2 E(S2)=σ2,在其他情况下 E ( S 2 ) E(S^2) E(S2)都是小于 σ 2 \sigma^2 σ2的。这一个结果也很好理解,只要样本均值 X ˉ \bar X Xˉ越偏离总体均值 μ \mu μ,样本也就越偏离总体均值。
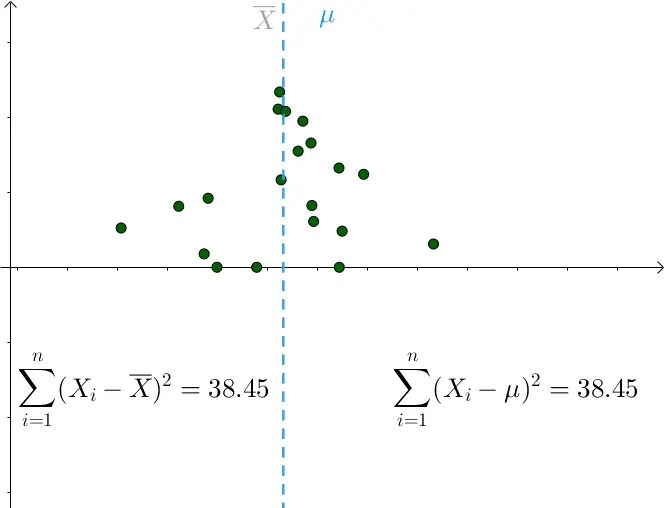
接下来就是要计算出差异 E [ ( X ˉ − μ ) 2 ] E \bigg [(\bar X - \mu)^2 \bigg ] E[(Xˉ−μ)2]是多少
由
E ( X ˉ ) = E ( 1 n ∑ i = 1 n X i ) = 1 n ∑ i = 1 n E ( X i ) = 1 n ∑ i = 1 n μ = μ E(\bar{X}) = E\bigg(\frac{1}{n} \sum_{i=1}^{n} X_i\bigg) = \frac{1}{n}\sum_{i=1}^nE(X_i) = \frac{1}{n}\sum_{i=1}^n \mu = \mu E(Xˉ)=E(n1i=1∑nXi)=n1i=1∑nE(Xi)=n1i=1∑nμ=μ
D ( a X i ) = a 2 D ( X i ) D(aX_i) = a^2 D(X_i) D(aXi)=a2D(Xi)
代入有:
E [ ( X ˉ − μ ) 2 ] = E [ ( X ˉ − E ( X ˉ ) ) 2 ] = D ( X ˉ ) = D ( 1 n ∑ i = 1 n X i ) = 1 n 2 ∑ i = 1 n D ( X i ) = 1 n 2 ⋅ n σ 2 = σ 2 n \begin{aligned} E \bigg [(\bar X - \mu)^2 \bigg ] &= E \bigg [(\bar X - E(\bar{X}))^2 \bigg ] \\ &=D(\bar{X})\\ &=D\bigg(\frac{1}{n} \sum_{i=1}^{n} X_i\bigg)\\ &=\frac{1}{n^2} \sum_{i=1}^{n} D(X_i) \\ &=\frac{1}{n^2} \cdot n \sigma^2 \\ &=\frac{\sigma^2}{n} \end{aligned} E[(Xˉ−μ)2]=E[(Xˉ−E(Xˉ))2]=D(Xˉ)=D(n1i=1∑nXi)=n21i=1∑nD(Xi)=n21⋅nσ2=nσ2
所以
E ( S 2 ) = σ 2 − E [ ( X ˉ − μ ) 2 ] = n − 1 n σ 2 E(S^2) = \sigma^2-E \bigg [(\bar X - \mu)^2 \bigg ] =\frac{n-1}{n}\sigma^2 E(S2)=σ2−E[(Xˉ−μ)2]=nn−1σ2
进行一下调整,即有
n n − 1 E ( S 2 ) = n n − 1 E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 ] = σ 2 \frac{n}{n-1}E(S^2)=\frac{n}{n-1} E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ]=E \left [ \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ]=\sigma^2 n−1nE(S2)=n−1nE[n1i=1∑n(Xi−Xˉ)2]=E[n−11i=1∑n(Xi−Xˉ)2]=σ2
这样得到的就是无偏的估计
https://www.zhihu.com/question/20099757
https://www.zhihu.com/question/22983179
